1 . 正多面体又称为柏拉图立体,是指一个多面体的所有面都是全等的正三角形或正多边形,每个顶点聚集的棱的条数都相等,这样的多面体就叫做正多面体.可以验证一共只有五种多面体.令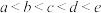 (
(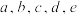 均为正整数),我们发现有时候某正多面体的所有顶点都可以和另一个正多面体的一些顶点重合,例如正
均为正整数),我们发现有时候某正多面体的所有顶点都可以和另一个正多面体的一些顶点重合,例如正 面体的所有顶点可以与正
面体的所有顶点可以与正 面体的某些顶点重合,正
面体的某些顶点重合,正 面体的所有顶点可以与正
面体的所有顶点可以与正 面体的所有顶点重合,等等.
面体的所有顶点重合,等等.
(1)当正 面体的所有顶点可以与正
面体的所有顶点可以与正 面体的某些顶点重合时,求正
面体的某些顶点重合时,求正 面体的棱与正
面体的棱与正 面体的面所成线面角的最大值;
面体的面所成线面角的最大值;
(2)当正 面体在棱长为
面体在棱长为 的正
的正 面体内,且正
面体内,且正 面体的所有顶点均为正
面体的所有顶点均为正 面体各面的中心时,求正
面体各面的中心时,求正 面体某一面所在平面截正
面体某一面所在平面截正 面体所得截面面积;
面体所得截面面积;
(3)已知正 面体的每个面均为正五边形,正
面体的每个面均为正五边形,正 面体的每个面均为正三角形.考生可在以下2问中选做1问.
面体的每个面均为正三角形.考生可在以下2问中选做1问.
(第一问答对得2分,第二问满分8分,两题均作答,以第一问结果给分)
第一问:求棱长为 的正
的正 面体的表面积;
面体的表面积;
第二问:求棱长为 的正
的正 面体的体积.
面体的体积.
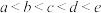 (
(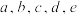 均为正整数),我们发现有时候某正多面体的所有顶点都可以和另一个正多面体的一些顶点重合,例如正
均为正整数),我们发现有时候某正多面体的所有顶点都可以和另一个正多面体的一些顶点重合,例如正 面体的所有顶点可以与正
面体的所有顶点可以与正 面体的某些顶点重合,正
面体的某些顶点重合,正 面体的所有顶点可以与正
面体的所有顶点可以与正 面体的所有顶点重合,等等.
面体的所有顶点重合,等等.(1)当正
 面体的所有顶点可以与正
面体的所有顶点可以与正 面体的某些顶点重合时,求正
面体的某些顶点重合时,求正 面体的棱与正
面体的棱与正 面体的面所成线面角的最大值;
面体的面所成线面角的最大值;(2)当正
 面体在棱长为
面体在棱长为 的正
的正 面体内,且正
面体内,且正 面体的所有顶点均为正
面体的所有顶点均为正 面体各面的中心时,求正
面体各面的中心时,求正 面体某一面所在平面截正
面体某一面所在平面截正 面体所得截面面积;
面体所得截面面积;(3)已知正
 面体的每个面均为正五边形,正
面体的每个面均为正五边形,正 面体的每个面均为正三角形.考生可在以下2问中选做1问.
面体的每个面均为正三角形.考生可在以下2问中选做1问.(第一问答对得2分,第二问满分8分,两题均作答,以第一问结果给分)
第一问:求棱长为
 的正
的正 面体的表面积;
面体的表面积;第二问:求棱长为
 的正
的正 面体的体积.
面体的体积.
您最近一年使用:0次
2023-11-10更新
|
556次组卷
|
3卷引用:重庆市乌江新高考协作体2024届高三上学期高考第一次联合调研抽测数学试题
重庆市乌江新高考协作体2024届高三上学期高考第一次联合调研抽测数学试题上海师范大学附属中学闵行分校2023-2024学年高二上学期期中数学试题(已下线)专题22 新高考新题型第19题新定义压轴解答题归纳(9大核心考点)(讲义)
名校
2 . 在正方体 中,
中, 是侧面
是侧面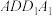 上一动点,下列结论正确的是( )
上一动点,下列结论正确的是( )
 中,
中, 是侧面
是侧面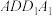 上一动点,下列结论正确的是( )
上一动点,下列结论正确的是( )A.三棱锥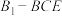 的体积为定值 的体积为定值 |
B.若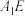 ∥ ∥ ,则 ,则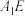  平面 平面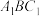 |
C.若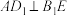 ,则 ,则 与平面 与平面 所成角为 所成角为 |
D.若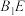 ∥平面 ∥平面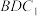 ,则 ,则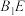 与 与 所成角的正弦最小值为 所成角的正弦最小值为 |
您最近一年使用:0次
2023-07-17更新
|
1106次组卷
|
5卷引用:重庆市第八中学校2023-2024学年高二上学期第一次月考数学试题
重庆市第八中学校2023-2024学年高二上学期第一次月考数学试题重庆市渝北中学校2024届高三上学期12月月考数学试题四川省宜宾市2022-2023学年高一下学期期末数学试题四川省成都外国语学校2023-2024学年高二上学期9月月考数学试题(已下线)第二章 立体几何中的计算 专题一 空间角 微点5 直线与平面所成角综合训练【培优版】
名校
3 . 如图,在四棱锥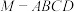 中,
中,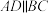 ,
,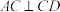 ,
,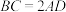 ,△MAD为等边三角形,平面
,△MAD为等边三角形,平面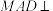 平面ABCD,点N在棱MD上,直线
平面ABCD,点N在棱MD上,直线 平面ACN.
平面ACN. .
.
(2)设二面角 的平面角为
的平面角为 ,直线CN与平面ABCD所成的角为
,直线CN与平面ABCD所成的角为 ,若
,若 的取值范围是
的取值范围是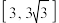 ,求
,求 的取值范围.
的取值范围.
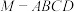 中,
中,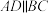 ,
,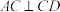 ,
,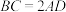 ,△MAD为等边三角形,平面
,△MAD为等边三角形,平面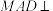 平面ABCD,点N在棱MD上,直线
平面ABCD,点N在棱MD上,直线 平面ACN.
平面ACN.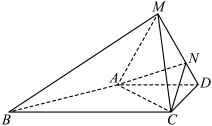
 .
.(2)设二面角
 的平面角为
的平面角为 ,直线CN与平面ABCD所成的角为
,直线CN与平面ABCD所成的角为 ,若
,若 的取值范围是
的取值范围是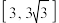 ,求
,求 的取值范围.
的取值范围.
您最近一年使用:0次
2023-06-30更新
|
2847次组卷
|
8卷引用:重庆市第八中学校2023-2024学年高二上学期开学适应性训练数学试题
名校
解题方法
4 . 如图,斜三棱柱 中,底面
中,底面 是正三角形,
是正三角形,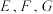 分别是侧棱
分别是侧棱 上的点,且
上的点,且 ,设直线
,设直线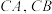 与平面
与平面 所成的角分别为
所成的角分别为 ,平面
,平面 与底面
与底面 所成的锐二面角为
所成的锐二面角为 ,则( )
,则( )
 中,底面
中,底面 是正三角形,
是正三角形,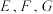 分别是侧棱
分别是侧棱 上的点,且
上的点,且 ,设直线
,设直线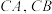 与平面
与平面 所成的角分别为
所成的角分别为 ,平面
,平面 与底面
与底面 所成的锐二面角为
所成的锐二面角为 ,则( )
,则( )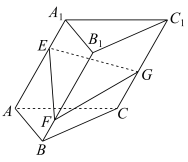
A.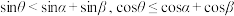 |
B.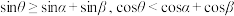 |
C.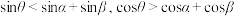 |
D.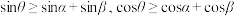 |
您最近一年使用:0次
2022-05-11更新
|
2406次组卷
|
11卷引用:重庆市第一中学教育共同体2022-2023学年高一下学期期中数学试题
重庆市第一中学教育共同体2022-2023学年高一下学期期中数学试题浙江省绍兴市柯桥区2022届高三下学期5月第二次适应性考试数学试题(已下线)专题23 立体几何中的压轴小题-2(已下线)考向27 空间点、直线、平面之间的位置关系(重点)(已下线)专题7-2 立体几何压轴小题:角度与动点、体积(讲+练)-1(已下线)专题7-2 立体几何压轴小题:角度与动点、体积(讲+练)-3(已下线)重难点突破05 立体几何中的常考压轴小题(七大题型)-2(已下线)专题14 立体几何常见压轴小题全归纳(练习)(已下线)第二章 立体几何中的计算 专题一 空间角 微点11 三正弦定理与三余弦定理(一)【培优版】(已下线)【讲】专题1 三角恒等变换问题(压轴小题)浙江省温州中学2023-2024学年高一下学期期中考试数学试题



