名校
1 . 如图,在四棱锥 中,底面
中,底面 是等腰梯形,
是等腰梯形, ,侧面
,侧面 平面
平面 分别为
分别为 的中点.
的中点. 平面
平面 .
.
(2)若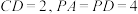 ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 中,底面
中,底面 是等腰梯形,
是等腰梯形, ,侧面
,侧面 平面
平面 分别为
分别为 的中点.
的中点.
 平面
平面 .
.(2)若
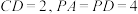 ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
2024-07-05更新
|
317次组卷
|
5卷引用:广西贵港市2023-2024年高二下学期期末教学质量监测数学试题
名校
解题方法
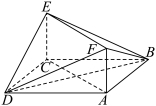
2 . 如图:底面 是菱形,
是菱形,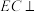 平面
平面 ,
, ,且
,且 .
.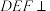 平面
平面 ;
;
(2)若二面角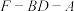 的余弦值为
的余弦值为 ,求直线
,求直线 与平面
与平面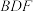 所成角的正弦值.
所成角的正弦值.
 是菱形,
是菱形,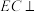 平面
平面 ,
, ,且
,且 .
.
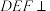 平面
平面 ;
;(2)若二面角
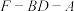 的余弦值为
的余弦值为 ,求直线
,求直线 与平面
与平面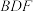 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
名校
解题方法
3 . 如图,在棱长为2的正方体 中,
中, 分别为
分别为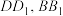 的中点,则下列选项正确的是( )
的中点,则下列选项正确的是( )
 中,
中, 分别为
分别为 的中点,则下列选项正确的是( )
的中点,则下列选项正确的是( )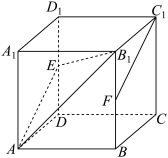
A.直线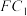 与直线 与直线 平行 平行 |
B.直线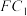 与底面 与底面 所成的角为 所成的角为 |
C.直线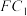 与直线 与直线 的距离为 的距离为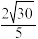 |
D.直线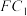 到平面 到平面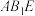 的距离为 的距离为 |
您最近一年使用:0次
2024-01-25更新
|
259次组卷
|
3卷引用:广西桂林市2023-2024学年高二上学期数学期末质量检测数学试题
广西桂林市2023-2024学年高二上学期数学期末质量检测数学试题(已下线)第七章 应用空间向量解立体几何问题拓展 专题二 平面法向量求法及其应用 微点3 平面法向量求法及其应用综合训练【基础版】浙江省杭州市严州中学新安江校区2024-2025学年高二上学期阶段性测试(返校考)数学试题
4 . 已知正方体 的棱长为1,
的棱长为1, 为棱
为棱 (包含端点)上的动点,下列命题正确的是( )
(包含端点)上的动点,下列命题正确的是( )
 的棱长为1,
的棱长为1, 为棱
为棱 (包含端点)上的动点,下列命题正确的是( )
(包含端点)上的动点,下列命题正确的是( )A.二面角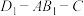 的大小为 的大小为 |
B.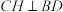 |
C.若 在正方形 在正方形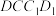 内部,且 内部,且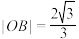 ,则点 ,则点 的轨迹长度为 的轨迹长度为 |
D.若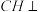 平面 平面 ,则直线 ,则直线 与平面 与平面 所成角的正弦值的取值范围为 所成角的正弦值的取值范围为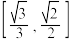 |
您最近一年使用:0次
名校
解题方法
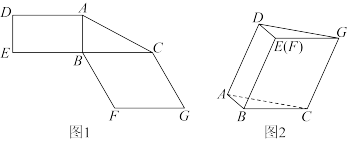
5 . 图1是由矩形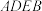 、
、 和菱形
和菱形 组成的一个平面图形,其中
组成的一个平面图形,其中 ,
,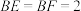 ,
, .将其沿
.将其沿 ,
, 折起使得
折起使得 与
与 重合,连接
重合,连接 ,如图2.
,如图2.
(1)证明:图2中的 ,
, ,
, ,
, 四点共面,且平面
四点共面,且平面 平面
平面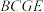 ;
;
(2)求图2中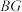 与平面
与平面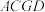 所成角的正弦值.
所成角的正弦值.
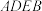 、
、 和菱形
和菱形 组成的一个平面图形,其中
组成的一个平面图形,其中 ,
,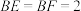 ,
,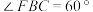 .将其沿
.将其沿 ,
, 折起使得
折起使得 与
与 重合,连接
重合,连接 ,如图2.
,如图2.
(1)证明:图2中的
 ,
, ,
, ,
, 四点共面,且平面
四点共面,且平面 平面
平面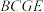 ;
;(2)求图2中
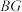 与平面
与平面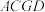 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
名校
6 . 如图, 底面
底面 ,
,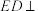 底面
底面 ,四边形
,四边形 是正方形,
是正方形, .
.
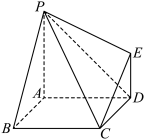
(1)证明: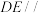 平面
平面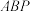 ;
;
(2)求直线 与平面
与平面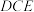 所成角的正切值.
所成角的正切值.
 底面
底面 ,
,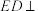 底面
底面 ,四边形
,四边形 是正方形,
是正方形, .
.
(1)证明:
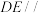 平面
平面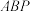 ;
;(2)求直线
 与平面
与平面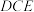 所成角的正切值.
所成角的正切值.
您最近一年使用:0次
2023-01-15更新
|
752次组卷
|
4卷引用:广西桂林市荔浦县荔城中学2022-2023学年高二上学期期末考试数学试题
广西桂林市荔浦县荔城中学2022-2023学年高二上学期期末考试数学试题广东省广州市2022-2023学年高二上学期期末数学试题(已下线)模块五 专题1 期末全真模拟(基础卷1)高二期末安徽省马鞍山市第二中学2022-2023学年高二下学期开学考试数学试题
名校
解题方法
7 . 如图,在三棱柱 中,
中, 平面ABC,
平面ABC,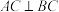 ,
,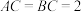 ,
,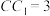 ,点D,E分别在棱
,点D,E分别在棱 和棱
和棱 上,且
上,且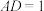 ,
,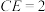 ,M为棱
,M为棱 的中点.
的中点.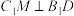 ;
;
(2)求直线AB与平面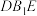 所成角的正弦值.
所成角的正弦值.
 中,
中, 平面ABC,
平面ABC,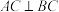 ,
,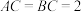 ,
,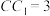 ,点D,E分别在棱
,点D,E分别在棱 和棱
和棱 上,且
上,且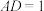 ,
,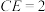 ,M为棱
,M为棱 的中点.
的中点.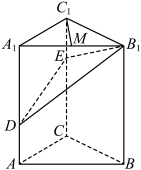
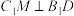 ;
;(2)求直线AB与平面
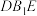 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
2023-05-24更新
|
1161次组卷
|
21卷引用:广西南宁市第三中学2022-2023学年高二下学期期末考试试题
广西南宁市第三中学2022-2023学年高二下学期期末考试试题广东省惠州市2021-2022学年高二上学期期末数学试题黑龙江省五校2021-2022学年高二上学期期末联考数学试题广东省深圳市第七高级中学2021-2022学年高二上学期期末数学试题上海市奉贤中学2021-2022学年高二下学期期末数学试题甘肃省武威市古浪县第二中学2021-2022学年高二上学期期末考试数学(理)试题(已下线)海南省华东师范大学第二附属中学乐东黄流中学2022-2023学年高二上学期12月教学质量监测(期末)数学试题黑龙江省七台河市勃利县高级中学2022-2023学年高二上学期期末考试数学试题四川省南充高级中学2022-2023学年高二上学期期末考试数学(理科)试题广西玉林市第十一中学2023-2024学年高二上学期10月月考数学试题广西壮族自治区玉林市第十一中学2024-2025学年高二上学期10月月考数学试题黑龙江省双鸭山市第一中学2021-2022学年高二上学期期中数学试题黑龙江省大庆市东风中学2021-2022学年高二下学期开学考试数学试题上海市行知中学2021-2022学年高二下学期3月月考数学试题重庆市第八中学校2021-2022学年高二艺术班下学期第二次月考数学试题广东省湛江市第二十一中学2022-2023学年高二下学期期中数学试题(已下线)模块三 专题4 空间向量的应用1直线与平面的夹角、二面角 B能力卷(已下线)模块三 专题5 直线与平面的夹角、二面角 B能力卷 (人教B)河南省新乡市长垣市第一中学2023-2024学年高三上学期10月月考数学试题天津市滨海新区实验中学滨海学校2024届高三上学期期中质量调查数学试题(已下线)通关练04 空间向量与立体几何大题9考点精练(41题)- 【考点通关】2023-2024学年高二数学高频考点与解题策略(人教A版2019选择性必修第一册)
名校
解题方法
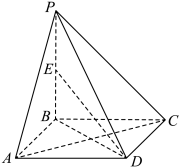
8 . 如图,四棱锥 ,底面
,底面 为正方形,
为正方形, 平面
平面 ,
, 为线段
为线段 的中点.
的中点.
(1)证明: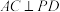 ;
;
(2)若 ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 ,底面
,底面 为正方形,
为正方形, 平面
平面 ,
, 为线段
为线段 的中点.
的中点.
(1)证明:
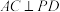 ;
;(2)若
 ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
2022-12-31更新
|
808次组卷
|
4卷引用:广西壮族自治区梧州市苍梧中学2022-2023学年高二上学期期末数学试题
名校
解题方法
9 . 已知在正方体 中,E,F,G分别是棱
中,E,F,G分别是棱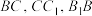 的中点.
的中点.
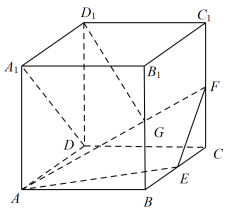
(1)证明: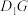 与平面
与平面 不平行;
不平行;
(2)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 中,E,F,G分别是棱
中,E,F,G分别是棱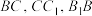 的中点.
的中点.
(1)证明:
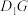 与平面
与平面 不平行;
不平行;(2)求直线
 与平面
与平面 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
2022-06-02更新
|
211次组卷
|
3卷引用:广西南宁市2021-2022学年高二下学期期末联考数学(理)试题
10 . 如图所示,四边形 为菱形,
为菱形, ,二面角
,二面角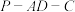 为直二面角,点
为直二面角,点 是棱
是棱 的中点.
的中点.
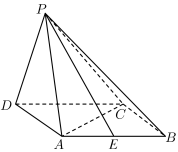
(1)求证: ;
;
(2)若 ,当二面角
,当二面角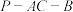 的正切值为
的正切值为 时,求直线
时,求直线 与平面
与平面 所成的角.
所成的角.
 为菱形,
为菱形, ,二面角
,二面角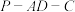 为直二面角,点
为直二面角,点 是棱
是棱 的中点.
的中点.
(1)求证:
 ;
;(2)若
 ,当二面角
,当二面角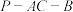 的正切值为
的正切值为 时,求直线
时,求直线 与平面
与平面 所成的角.
所成的角.
您最近一年使用:0次
2022-03-24更新
|
487次组卷
|
2卷引用:广西贺州市2021-2022学年高一下学期期末质量检测数学试题



