解题方法
1 . 若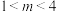 ,椭圆
,椭圆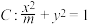 与双曲线
与双曲线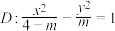 的离心率分别为
的离心率分别为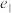 ,
,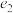 ,则
,则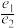 的最大值为
的最大值为______ .
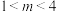 ,椭圆
,椭圆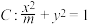 与双曲线
与双曲线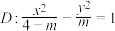 的离心率分别为
的离心率分别为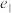 ,
,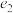 ,则
,则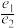 的最大值为
的最大值为
您最近一年使用:0次
解题方法
2 . 已知椭圆 ,双曲线
,双曲线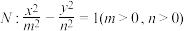 .设椭圆
.设椭圆 两个焦点分别为
两个焦点分别为 ,椭圆
,椭圆 的离心率为
的离心率为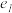 ,双曲线
,双曲线 的离心率为
的离心率为 ,记双曲线
,记双曲线 的一条渐近线与椭圆
的一条渐近线与椭圆 的一个交点为
的一个交点为 ,若
,若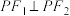 且
且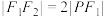 ,则
,则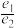 的值为
的值为__________ .
 ,双曲线
,双曲线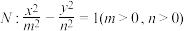 .设椭圆
.设椭圆 两个焦点分别为
两个焦点分别为 ,椭圆
,椭圆 的离心率为
的离心率为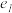 ,双曲线
,双曲线 的离心率为
的离心率为 ,记双曲线
,记双曲线 的一条渐近线与椭圆
的一条渐近线与椭圆 的一个交点为
的一个交点为 ,若
,若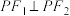 且
且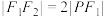 ,则
,则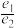 的值为
的值为
您最近一年使用:0次
23-24高二下·上海·期末
解题方法
3 . 已知椭圆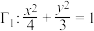 ,抛物线
,抛物线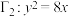 .若直线
.若直线 与曲线
与曲线 交于点
交于点 、
、 ,直线
,直线 与曲线
与曲线 分别交于点
分别交于点 、
、 .当
.当 时,则称直线
时,则称直线 是曲线
是曲线 与
与 的“等弦线”.
的“等弦线”.
(1)求椭圆 的离心率;
的离心率;
(2)直线 同时满足以下两个条件:①直线
同时满足以下两个条件:①直线 经过原点②直线
经过原点②直线 是
是 与
与 的“等弦线”.请求出
的“等弦线”.请求出 的方程;
的方程;
(3)已知点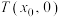 ,
,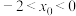 ,证明:过点
,证明:过点 存在
存在 与
与 的“等弦线”.
的“等弦线”.
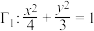 ,抛物线
,抛物线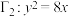 .若直线
.若直线 与曲线
与曲线 交于点
交于点 、
、 ,直线
,直线 与曲线
与曲线 分别交于点
分别交于点 、
、 .当
.当 时,则称直线
时,则称直线 是曲线
是曲线 与
与 的“等弦线”.
的“等弦线”.(1)求椭圆
 的离心率;
的离心率;(2)直线
 同时满足以下两个条件:①直线
同时满足以下两个条件:①直线 经过原点②直线
经过原点②直线 是
是 与
与 的“等弦线”.请求出
的“等弦线”.请求出 的方程;
的方程;(3)已知点
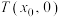 ,
,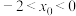 ,证明:过点
,证明:过点 存在
存在 与
与 的“等弦线”.
的“等弦线”.
您最近一年使用:0次
名校
4 . 椭圆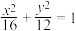 的离心率为
的离心率为________ .
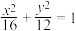 的离心率为
的离心率为
您最近一年使用:0次
名校
解题方法
5 . 设 ,
, 分别是椭圆
分别是椭圆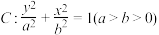 的右顶点和上焦点,点
的右顶点和上焦点,点 在
在 上,且
上,且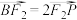 ,则
,则 的离心率为
的离心率为________ .
 ,
, 分别是椭圆
分别是椭圆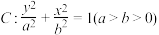 的右顶点和上焦点,点
的右顶点和上焦点,点 在
在 上,且
上,且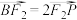 ,则
,则 的离心率为
的离心率为
您最近一年使用:0次
解题方法
6 . 阿波罗尼斯在对圆锥曲线的研究过程中,还进一步研究了圆锥曲线的光学性质,例如椭圆的光学性质:(如图1)从椭圆一个焦点发出的光线,经过椭圆反射后,反射光线交于椭圆的另一个焦点上.在对该性质证明的过程中(如图2),他还特别用到了“角平分线性质定理”: ,从而得到
,从而得到 ,而性质得证
,而性质得证
(1)如图3,已知椭圆 的左右焦点分别为
的左右焦点分别为 ,一束光线从
,一束光线从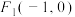 射出,经椭圆上
射出,经椭圆上 点反射:
点反射: 处法线(与椭圆
处法线(与椭圆 在
在 处切线垂直的直线)与
处切线垂直的直线)与 轴交于
轴交于 点,已知
点,已知 ,求椭圆
,求椭圆 方程(直接写出结果)
方程(直接写出结果) ,长轴长为
,长轴长为 ,焦距为
,焦距为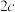 ,若一条光线从左焦点射出,经过椭圆上点若干次反射,第一次回到左焦点所经过的路程为
,若一条光线从左焦点射出,经过椭圆上点若干次反射,第一次回到左焦点所经过的路程为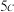 ,求椭圆的离心率
,求椭圆的离心率
(3)对于抛物线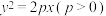 ,猜想并证明其光线性质.
,猜想并证明其光线性质.
 ,从而得到
,从而得到 ,而性质得证
,而性质得证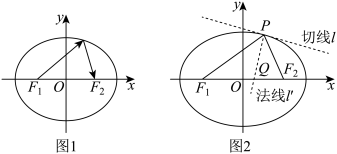
(1)如图3,已知椭圆
 的左右焦点分别为
的左右焦点分别为 ,一束光线从
,一束光线从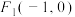 射出,经椭圆上
射出,经椭圆上 点反射:
点反射: 处法线(与椭圆
处法线(与椭圆 在
在 处切线垂直的直线)与
处切线垂直的直线)与 轴交于
轴交于 点,已知
点,已知 ,求椭圆
,求椭圆 方程(直接写出结果)
方程(直接写出结果)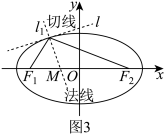
 ,长轴长为
,长轴长为 ,焦距为
,焦距为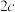 ,若一条光线从左焦点射出,经过椭圆上点若干次反射,第一次回到左焦点所经过的路程为
,若一条光线从左焦点射出,经过椭圆上点若干次反射,第一次回到左焦点所经过的路程为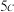 ,求椭圆的离心率
,求椭圆的离心率(3)对于抛物线
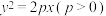 ,猜想并证明其光线性质.
,猜想并证明其光线性质.
您最近一年使用:0次
名校
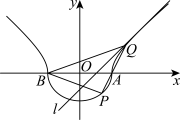
7 . 如图,由部分椭圆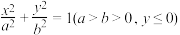 和部分双曲线
和部分双曲线 ,组成的曲线
,组成的曲线 称为“盆开线”.曲线
称为“盆开线”.曲线 与
与 轴有
轴有 两个交点,且椭圆与双曲线的离心率之积为
两个交点,且椭圆与双曲线的离心率之积为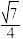 .
.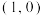 的直线
的直线 与
与 相切于点
相切于点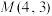 ,求部分椭圆方程、部分双曲线方程及直线
,求部分椭圆方程、部分双曲线方程及直线 的方程;
的方程;
(2)过 的直线
的直线 与
与 相交于点
相交于点 三点,求证:
三点,求证: .
.
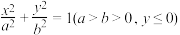 和部分双曲线
和部分双曲线 ,组成的曲线
,组成的曲线 称为“盆开线”.曲线
称为“盆开线”.曲线 与
与 轴有
轴有 两个交点,且椭圆与双曲线的离心率之积为
两个交点,且椭圆与双曲线的离心率之积为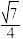 .
.
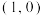 的直线
的直线 与
与 相切于点
相切于点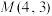 ,求部分椭圆方程、部分双曲线方程及直线
,求部分椭圆方程、部分双曲线方程及直线 的方程;
的方程;(2)过
 的直线
的直线 与
与 相交于点
相交于点 三点,求证:
三点,求证: .
.
您最近一年使用:0次
名校
解题方法
8 . 已知椭圆 经过直角三角形的直角顶点,且以另外两个顶点作为
经过直角三角形的直角顶点,且以另外两个顶点作为 的焦点,则
的焦点,则 的离心率的最小值为
的离心率的最小值为________ .
 经过直角三角形的直角顶点,且以另外两个顶点作为
经过直角三角形的直角顶点,且以另外两个顶点作为 的焦点,则
的焦点,则 的离心率的最小值为
的离心率的最小值为
您最近一年使用:0次
9 . 已知椭圆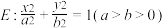 ,点
,点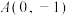 是椭圆中心与该椭圆一个顶点的中点,点
是椭圆中心与该椭圆一个顶点的中点,点 为椭圆与
为椭圆与 轴正半轴的交点,且离心率为
轴正半轴的交点,且离心率为 ,过点
,过点 的直线(与
的直线(与 轴不重合)交椭圆
轴不重合)交椭圆 于
于 ,
, 两点.
两点.
(1)求椭圆 的标准方程;
的标准方程;
(2)直线 和直线
和直线 的斜率之积是否为定值?若是,求出这个值,若不是请说明理由;
的斜率之积是否为定值?若是,求出这个值,若不是请说明理由;
(3)若圆 的方程为
的方程为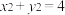 ,直线
,直线 ,
, 分别交圆
分别交圆 于
于 ,
, 两点,试证明:直线
两点,试证明:直线 恒过定点.
恒过定点.
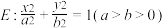 ,点
,点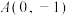 是椭圆中心与该椭圆一个顶点的中点,点
是椭圆中心与该椭圆一个顶点的中点,点 为椭圆与
为椭圆与 轴正半轴的交点,且离心率为
轴正半轴的交点,且离心率为 ,过点
,过点 的直线(与
的直线(与 轴不重合)交椭圆
轴不重合)交椭圆 于
于 ,
, 两点.
两点.(1)求椭圆
 的标准方程;
的标准方程;(2)直线
 和直线
和直线 的斜率之积是否为定值?若是,求出这个值,若不是请说明理由;
的斜率之积是否为定值?若是,求出这个值,若不是请说明理由;(3)若圆
 的方程为
的方程为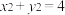 ,直线
,直线 ,
, 分别交圆
分别交圆 于
于 ,
, 两点,试证明:直线
两点,试证明:直线 恒过定点.
恒过定点.
您最近一年使用:0次
10 . 已知椭圆以原点为中心,焦点在 轴上,长半轴的长为6,离心率为
轴上,长半轴的长为6,离心率为 ,则椭圆的标准方程
,则椭圆的标准方程__________ .
 轴上,长半轴的长为6,离心率为
轴上,长半轴的长为6,离心率为 ,则椭圆的标准方程
,则椭圆的标准方程
您最近一年使用:0次
2024-04-17更新
|
337次组卷
|
3卷引用:上海市市北中学2023-2024学年高二下学期期中考试数学试题
上海市市北中学2023-2024学年高二下学期期中考试数学试题(已下线)专题02圆锥曲线全章复习攻略--高二期末考点大串讲(沪教版2020选修一)上海市上海交通大学附属中学闵行分校2024-2025学年高二上学期10月月考数学试卷



