2020高三·全国·专题练习
名校
解题方法
1 . 已知椭圆 :
: (
( )的四个顶点组成的四边形的面积为
)的四个顶点组成的四边形的面积为 ,且经过点
,且经过点 .过椭圆右焦点
.过椭圆右焦点 作直线
作直线 与椭圆
与椭圆 交于
交于 、
、 两点.
两点.
(1)求椭圆 的方程;
的方程;
(2)若 ,求直线
,求直线 的方程.
的方程.
 :
: (
( )的四个顶点组成的四边形的面积为
)的四个顶点组成的四边形的面积为 ,且经过点
,且经过点 .过椭圆右焦点
.过椭圆右焦点 作直线
作直线 与椭圆
与椭圆 交于
交于 、
、 两点.
两点.(1)求椭圆
 的方程;
的方程;(2)若
 ,求直线
,求直线 的方程.
的方程.
您最近一年使用:0次
2020-12-06更新
|
2292次组卷
|
13卷引用:黑龙江省双鸭山市饶河县高级中学2021-2022学年高二上学期期末数学试题
黑龙江省双鸭山市饶河县高级中学2021-2022学年高二上学期期末数学试题(已下线)专题52 平面解析几何专题训练-2021年高考一轮数学(文)单元复习一遍过(已下线)专题55 平面解析几何专题训练-2021年高考一轮数学单元复习一遍过(新高考地区专用)(已下线)专题55 平面解析几何专题训练-2021年高考一轮数学(理)单元复习一遍过吉林省四平市公主岭市范家屯镇第一中学两校联考2021届高三上学期期末数学(理)试题吉林省四平市公主岭市范家屯镇第一中学两校联考2021届高三上学期期末数学(文)试题陕西省宝鸡市金台区2020-2021学年高二上学期期末数学(文)试题(已下线)专题12 选择性必修第一册综合练习-(新教材)2020-2021学年高二数学单元复习(人教A版选择性必修第一册)(已下线)第3章 圆锥曲线的方程-2021-2022学年高二数学课后培优练(人教A版2019选择性必修第一册)(已下线)选择性必修第一册 综合测试(基础)-2021-2022学年高二数学一隅三反系列(人教A版2019选择性必修第一册)广东省广州市增城区增城中学2021-2022学年高二上学期第二阶段测试数学试题(已下线)第29节 椭圆江西省南昌市第三中学2022-2023学年高二上学期期中考试数学试题
真题
名校
2 . 已知椭圆C: 的离心率为
的离心率为 ,且过点
,且过点 .
.
(1)求 的方程:
的方程:
(2)点 ,
, 在
在 上,且
上,且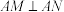 ,
, ,
, 为垂足.证明:存在定点
为垂足.证明:存在定点 ,使得
,使得 为定值.
为定值.
 的离心率为
的离心率为 ,且过点
,且过点 .
.(1)求
 的方程:
的方程:(2)点
 ,
, 在
在 上,且
上,且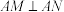 ,
, ,
, 为垂足.证明:存在定点
为垂足.证明:存在定点 ,使得
,使得 为定值.
为定值.
您最近一年使用:0次
2020-07-09更新
|
48499次组卷
|
107卷引用:黑龙江省双鸭山市第一中学2020-2021学年高二上学期期中考试数学(理)试题
黑龙江省双鸭山市第一中学2020-2021学年高二上学期期中考试数学(理)试题黑龙江省大庆市铁人中学2020-2021学年高二上学期期末考试数学(文)试题黑龙江省七台河市勃利县高级中学2022-2023学年高二上学期期末考试数学试题2020年新高考全国卷Ⅰ数学试题(山东卷)(已下线)专题05 平面解析几何——2020年高考真题和模拟题理科数学分项汇编专题07+解析几何-2021高考数学(理)高频考点、热点题型归类强化(已下线)专题05 平面解析几何——2020年高考真题和模拟题文科数学分项汇编(已下线)易错点09 解析几何-备战2021年新高考数学一轮复习易错题(已下线)专题08 平面解析几何(解答题)——三年(2018-2020)高考真题理科数学分项汇编(已下线)专题08 平面解析几何(解答题)——三年(2018-2020)高考真题文科数学分项汇编(已下线)考点27 椭圆的综合问题-2021年高考数学三年真题与两年模拟考点分类解读(新高考地区专用)(已下线)考点45 三定问题(定点、定值、定直线)(讲解)-2021年高考数学复习一轮复习笔记(已下线)专题29 圆锥曲线的综合问题-十年(2011-2020)高考真题数学分项(已下线)专题15 直线与椭圆、抛物线的位置关系-2021年浙江省高考数学命题规律大揭秘【学科网名师堂】(已下线)考点41 直线与圆锥曲线的位置关系-备战2021年高考数学(理)一轮复习考点一遍过(已下线)考点39 直线与圆锥曲线的位置关系-备战2021年高考数学(文)一轮复习考点一遍过(已下线)易错点12 圆锥曲线-备战2021年高考数学(理)一轮复习易错题(已下线)易错点12 圆锥曲线-备战2021年高考数学(文)一轮复习易错题北京师范大学附属实验中学2020-2021学年高二数学12月月考试题山东省济宁市兖州区2020-2021学年高二上学期期中考试数学试题(已下线)专题9.7 圆锥曲线综合问题(精讲)-2021年新高考数学一轮复习学与练(已下线)专题9.7 圆锥曲线综合问题(练)-2021年新高考数学一轮复习讲练测(已下线)考点35 椭圆的标准方程及几何性质-备战2021年新高考数学一轮复习考点一遍过(已下线)模块检测卷三(A卷 基础过关检查)-2021年高考数学一轮复习单元滚动双测卷(新高考地区专用)西藏日喀则市第二高级中学2021届高三上学期期中考试数学(理)试题(已下线)精做05 解析几何-备战2021年高考数学(理)大题精做(已下线)精做05 解析几何-备战2021年高考数学大题精做(新高考专用)(已下线)专题4.5 圆锥曲线-2021年高考数学解答题挑战满分专项训练(新高考地区专用)(已下线)专题12 解析几何中的定值、定点和定线问题 第一篇 热点、难点突破篇(讲)-2021年高考数学二轮复习讲练测(浙江专用)(已下线) 专题22 圆锥曲线的“三定”与探索性问题(练)-2021年高三数学二轮复习讲练测(新高考版)(已下线)专题26 圆锥曲线的“三定”与探索性问题(练)-2021年高三数学二轮复习讲练测( 文理通用)(已下线)解密12 圆锥曲线中的热点问题(讲义)-【高频考点解密】2021年新高考数学二轮复习讲义+分层训练(已下线)专题3.1 椭圆-2020-2021学年高二数学同步课堂帮帮帮(人教A版2019选择性必修第一册)(已下线)专题12 圆锥曲线 -备战2021年新高考数学纠错笔记 (已下线)数学-2021年高考考前20天终极冲刺攻略(三)(新高考地区专用)【学科网名师堂】 (5月30日)(已下线)数学-2021年高考考前20天终极冲刺攻略(二)(新高考地区专用)【学科网名师堂】 (5月28日)四川省内江市威远中学2020-2021学年高三1月月考数学(理)试题(已下线)预测10 圆锥曲线中的综合性问题-【临门一脚】2021年高考数学三轮冲刺过关(新高考专用)【学科网名师堂】(已下线)押新高考第21题 圆锥曲线-备战2021年高考数学临考题号押题(新高考专用)北师大版(2019) 选修第一册 必杀技 第二章 素养检测苏教版(2019) 选修第一册 必杀技 第三章 素养检测苏教版(2019) 选修第一册 突围者 第3章 章末培优专练(已下线)考点40 椭圆-备战2022年高考数学(理)一轮复习考点帮(已下线)考点38 椭圆-备战2022年高考数学(文)一轮复习考点帮北师大版(2019) 选修第一册 突围者 第二章 章末培优专练苏教版(2019) 选修第一册 一蹴而就 第3章 单元整合(已下线)专题9.7 圆锥曲线综合问题 2022年高考数学一轮复习讲练测(新教材新高考)(练)福建省福州市八校联考2021-2022学年高二上学期期中考试数学试题福建省厦门双十中学2021-2022学年高二上学期期中考试数学试题人教B版(2019) 选修第一册 过关检测 第二章 专项把关练(已下线)专题20 椭圆、抛物线(解答题)-备战2022年高考数学(理)母题题源解密(全国甲卷)(已下线)2020年新高考全国1数学高考真题变式题17-22题(已下线)专题21 椭圆、抛物线(解答题)-备战2022年高考数学(文)母题题源解密(全国甲卷)(已下线)第3讲 圆锥曲线中的证明、定值、定点问题(讲)-2022年高考数学二轮复习讲练测(新教材·新高考地区专用)(已下线)解密14 椭圆及其方程(讲义)-【高频考点解密】2022年高考数学二轮复习讲义+分层训练(新高考专用)(已下线)专题12解析几何中的定值、定点和定线问题(讲)--第一篇 热点、难点突破篇-《2022年高考数学二轮复习讲练测(浙江专用)》(已下线)专题43 巧解圆锥曲线中的定点和定值问题-学会解题之高三数学万能解题模板【2022版】(已下线)第三章 圆锥曲线与方程(选拔卷)-【单元测试】2021-2022学年高二数学尖子生选拔卷(苏教版2019选择性必修第一册)(已下线)专题27 圆锥曲线(文科)解答题20题-备战2022年高考数学冲刺横向强化精练精讲(已下线)专题26 圆锥曲线(理科)解答题20题-备战2022年高考数学冲刺横向强化精练精讲(已下线)类型五 定值问题-【题型突破】备战2022年高考数学二轮基础题型+重难题型突破(新高考专用)(已下线)专题44 盘点圆锥曲线中的定值问题——备战2022年高考数学二轮复习常考点专题突破(已下线)解密14 圆锥曲线(讲义)-【高频考点解密】2022年高考数学二轮复习讲义+分层训练(浙江专用)(已下线)押全国卷(文科)第20题 圆锥曲线-备战2022年高考数学(文)临考题号押题(全国卷)(已下线)2022年高考考前20天终极冲刺攻略(三)【数学】(新高考地区专用)(5月29日)(已下线)专题58:直线与椭圆的位置关系-2023届高考数学一轮复习精讲精练(新高考专用)(已下线)专题19 圆锥曲线解答题(已下线)专题17 解析几何解答题2023版 北师大版(2019) 选修第一册 突围者 第二章 章末培优专练(已下线)2020年高考山东卷数学一题多解(已下线)专题10 解几定值考频高,特殊情况先出招(已下线)考向36 圆锥曲线中的定点、定值问题(重点)山东省德州市临邑县第一中学2022-2023学年高二上学期10月月考数学试题湖南省邵阳市武冈市2022-2023学年高二上学期期中数学试题(已下线)专题9-5 圆锥曲线大题基础:定点归类(已下线)专题21 解析几何中的定点与定值问题(已下线)专题8 解析几何 第4讲 圆锥曲线中的定点,定值,探究性问题广东省汕头市潮阳一中明光学校2023届高三教学质量监测数学试题湖北省荆州市沙市中学2022-2023学年高二下学期2月月考数学试题(已下线)模块三 专题8 解析几何(已下线)押新高考第21题 圆锥曲线(已下线)专题24 圆锥曲线八类压轴题(解答题)-3专题07平面解析几何(成品)专题07平面解析几何(添加试题分类成品)(已下线)第五篇 向量与几何 专题8 帕斯卡定理、布列安桑定理、笛沙格定理、彭塞列闭合定理 微点4 塞瓦定理、富瑞基尔定理江西省上高二中2022-2023学年高二上学期第三次月考(12月)数学试题甘肃省酒泉市实验中学2023-2024学年高二上学期期中数学试题山西省朔州市怀仁市第九中学高中部2023-2024学年高二上学期期中数学试题宁夏银川市永宁县上游高级中学2023-2024学年高二上学期月考(二)数学试题湖南省常德市第一中学2023-2024学年高二上学期第二次月水平检测(12月)数学试题天津市第一中学滨海学校2024届高三第四次学业水平质量调查数学试卷(已下线)四川省成都市第七中学2023-2024学年高二上学期期末复习数学试题(四)河南省南阳市第一中学校2023-2024学年高二下学期开学考试数学试题(已下线)专题08 圆锥曲线 第二讲 圆锥曲线中的定点、定直线与定值问题(解密讲义)(已下线)大招18非对称处理四川省成都外国语学校2024届高三下学期高考模拟(二)数学(理科)试题四川省成都外国语学校2024届高三下学期高考模拟(二)数学(文科)试题(已下线)压轴小题12 椭圆中的定值与夹角问题(压轴小题)(已下线)专题24 解析几何解答题(文科)-3(已下线)专题04 高考解几大题真题精练(已下线)专题24 解析几何解答题(理科)-3四川省雅安市神州天立学校2024届高三高考适应性考试(三)数学(文)试题(已下线)五年新高考专题10平面解析几何(已下线)专题3 曲线系方程及其应用【练】(压轴题大全)四川省雅安市神州天立学校2024届高三下学期高考冲刺热身(四)数学(理)试题广东省汕头市南澳县南澳中学2024届高三下学期冲刺高考模拟考试数学试题【巩固卷】第3章圆锥曲线与方程高考强化 单元测试B-湘教版(2019)选择性必修第一册
解题方法
3 . 已知中心在原点,焦点在 轴上,离心率为
轴上,离心率为 的椭圆过点
的椭圆过点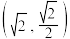 .
.
(1)求椭圆方程;
(2)设不过原点O的直线 ,与该椭圆交于P、Q两点,直线OP、OQ的斜率依次为
,与该椭圆交于P、Q两点,直线OP、OQ的斜率依次为 ,满足
,满足 ,求
,求 的值.
的值.
 轴上,离心率为
轴上,离心率为 的椭圆过点
的椭圆过点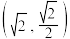 .
.(1)求椭圆方程;
(2)设不过原点O的直线
 ,与该椭圆交于P、Q两点,直线OP、OQ的斜率依次为
,与该椭圆交于P、Q两点,直线OP、OQ的斜率依次为 ,满足
,满足 ,求
,求 的值.
的值.
您最近一年使用:0次
2018-10-01更新
|
352次组卷
|
2卷引用:黑龙江省海林市朝鲜族中学人教版高中数学选修1-1同步练习:模块终结测评(一)
2010·山东聊城·二模
解题方法
4 . 已知椭圆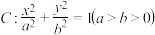 经过点
经过点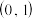 ,离心率为
,离心率为 .
.
(1)求椭圆 的方程;
的方程;
(2)设直线 与椭圆
与椭圆 交于
交于 、
、 ,点
,点 关于
关于 轴的对称点
轴的对称点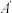 (
(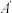 与
与 不重合),则直线
不重合),则直线 与
与 轴是否交于一定点?若是,请写出定点坐标,并证明你的结论;若不是,请说明理由.
轴是否交于一定点?若是,请写出定点坐标,并证明你的结论;若不是,请说明理由.
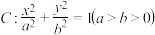 经过点
经过点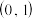 ,离心率为
,离心率为 .
.(1)求椭圆
 的方程;
的方程;(2)设直线
 与椭圆
与椭圆 交于
交于 、
、 ,点
,点 关于
关于 轴的对称点
轴的对称点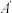 (
(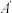 与
与 不重合),则直线
不重合),则直线 与
与 轴是否交于一定点?若是,请写出定点坐标,并证明你的结论;若不是,请说明理由.
轴是否交于一定点?若是,请写出定点坐标,并证明你的结论;若不是,请说明理由.
您最近一年使用:0次
2016-11-30更新
|
1545次组卷
|
10卷引用:2012年全国高中数学联赛黑龙江赛区预赛试题



