名校
解题方法
1 . 已知椭圆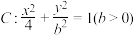 的左、右焦点分别为
的左、右焦点分别为 ,过
,过 上的一点
上的一点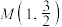 作
作 的切线
的切线 ,点
,点 关于
关于 的对称点分别为
的对称点分别为 ,则四边形
,则四边形 的面积为
的面积为________ .
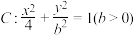 的左、右焦点分别为
的左、右焦点分别为 ,过
,过 上的一点
上的一点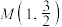 作
作 的切线
的切线 ,点
,点 关于
关于 的对称点分别为
的对称点分别为 ,则四边形
,则四边形 的面积为
的面积为
您最近一年使用:0次
名校
解题方法
2 . 已知椭圆C: 过点
过点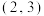 ,且C的右焦点为
,且C的右焦点为 .
.
(1)求C的离心率;
(2)过点F且斜率为1的直线与C交于M,N两点,P直线 上的动点,记直线PM,PN,PF的斜率分别为
上的动点,记直线PM,PN,PF的斜率分别为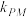 ,
, ,
,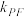 ,证明:
,证明: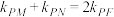 .
.
 过点
过点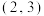 ,且C的右焦点为
,且C的右焦点为 .
.(1)求C的离心率;
(2)过点F且斜率为1的直线与C交于M,N两点,P直线
 上的动点,记直线PM,PN,PF的斜率分别为
上的动点,记直线PM,PN,PF的斜率分别为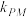 ,
, ,
,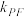 ,证明:
,证明: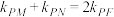 .
.
您最近一年使用:0次
2023-09-10更新
|
1313次组卷
|
8卷引用:河南省天一联考2023-2024学年高三上学期调研考试数学试题
河南省天一联考2023-2024学年高三上学期调研考试数学试题河南省安阳市第一中学等十所名校2023-2024学年高中毕业班阶段性测试(一)数学试题陕西省商洛市部分学校2023-2024学年高三上学期10月阶段性测试(一)理科数学试题陕西省商洛市部分学校2023-2024学年高三上学期10月阶段性测试(一)文科数学试题(已下线)重难专攻(十一)?圆锥曲线中的证明,探究性问题(A素养养成卷)(已下线)重难点突破09 一类与斜率和、差、商、积问题的探究(四大题型)内蒙古赤峰市赤峰二中2024届高三上学期第三次月考数学(文)试题(已下线)第三章 圆锥曲线的方程(知识归纳+题型突破)-2023-2024学年高二数学单元速记·巧练(人教A版2019选择性必修第一册)
3 . 已知 是椭圆
是椭圆 上的两点,
上的两点,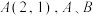 关于原点
关于原点 对称,
对称, 是椭圆
是椭圆 上异于
上异于 的一点,直线
的一点,直线 和
和 的斜率满足
的斜率满足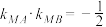 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)若斜率存在且不经过原点的直线 交椭圆
交椭圆 于
于 两点
两点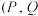 异于椭圆
异于椭圆 的上、下顶点),当
的上、下顶点),当 的面积最大时,求
的面积最大时,求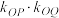 的值.
的值.
 是椭圆
是椭圆 上的两点,
上的两点,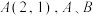 关于原点
关于原点 对称,
对称, 是椭圆
是椭圆 上异于
上异于 的一点,直线
的一点,直线 和
和 的斜率满足
的斜率满足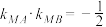 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)若斜率存在且不经过原点的直线
 交椭圆
交椭圆 于
于 两点
两点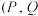 异于椭圆
异于椭圆 的上、下顶点),当
的上、下顶点),当 的面积最大时,求
的面积最大时,求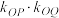 的值.
的值.
您最近一年使用:0次
2023-09-08更新
|
1734次组卷
|
8卷引用:河南省信阳高级中学2023-2024学年高三上学期9月一模数学试题
(已下线)河南省信阳高级中学2023-2024学年高三上学期9月一模数学试题河南省周口市项城市2024届高三5校青桐鸣大联考9月数学试题(已下线)3.1.2 椭圆的简单的几何性质(AB分层训练)-【冲刺满分】2023-2024学年高二数学重难点突破+分层训练同步精讲练(人教A版2019选择性必修第一册)(已下线)专题突破卷23 圆锥曲线大题归类(已下线)考点16 解析几何中的定值问题 2024届高考数学考点总动员(已下线)重难点突破09 一类与斜率和、差、商、积问题的探究(四大题型)(已下线)考点18 解析几何中的范围、最值问题 2024届高考数学考点总动员(已下线)专题06 椭圆的压轴题(6类题型+过关检测)-【常考压轴题】2023-2024学年高二数学上学期压轴题攻略(人教A版2019选择性必修第一册)
4 . 已知过点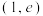 的椭圆
的椭圆 :
: 的焦距为2,其中
的焦距为2,其中 为椭圆
为椭圆 的离心率.
的离心率.
(1)求 的标准方程;
的标准方程;
(2)设 为坐标原点,直线
为坐标原点,直线 与
与 交于
交于 两点,以
两点,以 ,
, 为邻边作平行四边形
为邻边作平行四边形 ,且点
,且点 恰好在
恰好在 上,试问:平行四边形
上,试问:平行四边形 的面积是否为定值?若是定值,求出此定值;若不是,说明理由.
的面积是否为定值?若是定值,求出此定值;若不是,说明理由.
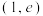 的椭圆
的椭圆 :
: 的焦距为2,其中
的焦距为2,其中 为椭圆
为椭圆 的离心率.
的离心率.(1)求
 的标准方程;
的标准方程;(2)设
 为坐标原点,直线
为坐标原点,直线 与
与 交于
交于 两点,以
两点,以 ,
, 为邻边作平行四边形
为邻边作平行四边形 ,且点
,且点 恰好在
恰好在 上,试问:平行四边形
上,试问:平行四边形 的面积是否为定值?若是定值,求出此定值;若不是,说明理由.
的面积是否为定值?若是定值,求出此定值;若不是,说明理由.
您最近一年使用:0次
2023-03-14更新
|
2000次组卷
|
10卷引用:河南省南阳市第一中学校2022-2023学年下期高二第四次月考数学试题
河南省南阳市第一中学校2022-2023学年下期高二第四次月考数学试题云南省昆明市2023届“三诊一模”高三复习教学质量检测数学陕西省汉中市2023届高三下学期第二次教学质量检测理科数学试题湖北省武汉市武钢三中2022-2023学年高二下学期3月月考数学试题(已下线)专题16圆锥曲线(解答题)宁夏吴忠市吴忠中学2022-2023学年高二下学期期末考试数学(理)试题四川省宜宾市叙州区第二中学校2022-2023学年高二下学期3月月考数学(理)试题2024届高三高考模拟综合测试数学试题(一)(已下线)专题15 圆锥曲线综合(已下线)选择性必修一 综合测试-2023-2024学年高二数学同步精品课堂(人教B版2019选择性必修第一册)
10-11高三上·福建泉州·期中
名校
解题方法
5 . 已知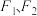 为椭圆
为椭圆 的左、右焦点,点
的左、右焦点,点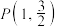 为椭圆上一点,且
为椭圆上一点,且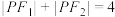
(1)求椭圆 的标准方程;
的标准方程;
(2)若圆 是以
是以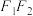 为直径的圆,直线
为直径的圆,直线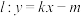 与圆
与圆 相切,并与椭圆
相切,并与椭圆 交于不同的两点
交于不同的两点 、
、 ,且
,且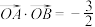 ,求
,求 的值
的值
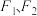 为椭圆
为椭圆 的左、右焦点,点
的左、右焦点,点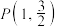 为椭圆上一点,且
为椭圆上一点,且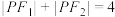
(1)求椭圆
 的标准方程;
的标准方程;(2)若圆
 是以
是以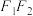 为直径的圆,直线
为直径的圆,直线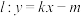 与圆
与圆 相切,并与椭圆
相切,并与椭圆 交于不同的两点
交于不同的两点 、
、 ,且
,且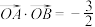 ,求
,求 的值
的值
您最近一年使用:0次
2022-12-08更新
|
485次组卷
|
23卷引用:河南省洛阳市宜阳县第一高级中学2022-2023学年高二上学期清北园第三次能力达标检测文科数学试题
河南省洛阳市宜阳县第一高级中学2022-2023学年高二上学期清北园第三次能力达标检测文科数学试题河南省洛阳市宜阳第一高级中学2022-2023学年高二上学期第三次月考数学试题(文)(已下线)2011届福建省泉州外国语中学高三上学期期中考试数学文卷(已下线)2015届山东师范大学附属中学高三第一次模拟考试理科数学试卷(已下线)2015届山东师范大学附属中学高三第一次模拟考试文科数学试卷2015届新疆师范大学附属中学高三12月月考文科数学试卷12015届新疆师范大学附属中学高三12月月考文科数学试卷22017届陕西省黄陵中学高三(重点班)4月月考(高考全国统一全真模拟二)数学(文)试卷四川省成都双流棠湖中学2017-2018年高二10月月考(文科)重庆市第一中学2018届高三11月月考数学(文)试题(已下线)黄金30题系列 高二年级数学(理) 大题好拿分【基础版】【全国百强校】西藏自治区拉萨中学2019届高三第四次月考数学(文)试题河北省唐县一中2018-2019学年高二上学期期中考试数学(文)试题河北省唐县一中2018-2019学年高二上学期期中考试数学(理)试题河北省石家庄市第二十七中学2020-2021学年高二上学期段考一(10月)数学试题湖北省荆州市沙市五中2020-2021学年高二下学期3月月考数学试题(已下线)第3章 圆锥曲线与方程(基础卷)-2021-2022学年高二数学新教材单元双测卷(苏教版2019选择性必修第一册)(已下线)第3章 圆锥曲线与方程 单元综合检测(能力提升)(单元培优)-2021-2022学年高二数学课后培优练(苏教版2019选择性必修第一册)江苏省连云港市灌南高级中学2021-2022学年高二上学期第一次月考数学试题四川省凉山州冕宁中学2022-2023学年高二上学期12月月考数学试题浙江省嘉兴市海盐第二高级中学2022-2023学年高二上学期10月第一阶段检测数学试题重庆市綦江南州中学校2022-2023学年高二上学期期末数学试题浙江省嘉兴市桐乡市茅盾中学2023-2024学年高二上学期第一次考试数学试题
名校
解题方法
6 . 已知椭圆 的中心为坐标原点,对称轴为
的中心为坐标原点,对称轴为 轴,
轴, 轴,且过
轴,且过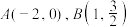 两点.
两点.
(1)求椭圆 的方程;
的方程;
(2) 为椭圆
为椭圆 的右焦点,直线
的右焦点,直线 交椭圆
交椭圆 于
于 (不与点
(不与点 重合)两点,记直线
重合)两点,记直线 的斜率分别为
的斜率分别为 ,若
,若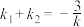 ,证明:
,证明: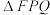 的周长为定值,并求出定值.
的周长为定值,并求出定值.
 的中心为坐标原点,对称轴为
的中心为坐标原点,对称轴为 轴,
轴, 轴,且过
轴,且过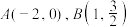 两点.
两点.(1)求椭圆
 的方程;
的方程;(2)
 为椭圆
为椭圆 的右焦点,直线
的右焦点,直线 交椭圆
交椭圆 于
于 (不与点
(不与点 重合)两点,记直线
重合)两点,记直线 的斜率分别为
的斜率分别为 ,若
,若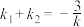 ,证明:
,证明: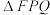 的周长为定值,并求出定值.
的周长为定值,并求出定值.
您最近一年使用:0次
2022-09-28更新
|
3324次组卷
|
17卷引用:河南省周口恒大中学2022-2023学年高二上学期期末考试数学试题
河南省周口恒大中学2022-2023学年高二上学期期末考试数学试题河南省南阳市第一中学校2023届高三下学期开学考试理科数学试题河南省南阳市宛城区南阳市第一中学校2023届高三下学期开学考试文科数学试题河南省周口市川汇区周口恒大中学2023-2024学年高二上学期12月月考数学试题河南省信阳市新县高级中学2024届高三下学期模拟考试一数学试题重庆市第八中学校2023届高三上学期高考适应性月考(一)数学试题湖北省武汉市第一中学2022-2023学年高三上学期10月月考数学试题辽宁省葫芦岛市四校2022-2023学年高二上学期期中联考数学试题(已下线)专题32 一类与斜率和、差、商、积问题的探究-1湖南师范大学附属中学2022-2023学年高三上学期月考(三)数学试题湖南省衡阳师范学院祁东附属中学2023届高三下学期2月高考模拟数学试题河北省石家庄市第二中学2022-2023学年高三上学期期中考试数学试题(已下线)广东省2022届高三一模数学试题变式题17-22安徽省安庆市第二中学2022-2023学年高三下学期第七次质量检测数学试题(已下线)专题3.16 圆锥曲线中的定点、定值、定直线问题大题专项训练(30道)-2022-2023学年高二数学举一反三系列(人教A版2019选择性必修第一册)(已下线)专题3.5 直线与椭圆的位置关系-重难点题型精讲-2022-2023学年高二数学举一反三系列(人教A版2019选择性必修第一册)(已下线)专题09 椭圆中定点定值定线四种考法-【常考压轴题】(苏教版2019选择性必修第一册)
名校
解题方法
7 . 已知椭圆C: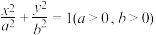 的长轴为双曲线
的长轴为双曲线 的实轴,且椭圆C过点
的实轴,且椭圆C过点 .
.
(1)求椭圆C的标准方程;
(2)点A,B是椭圆C上异于点P的两个不同的点,直线PA与PB的斜率均存在,分别记为 ,且
,且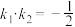 ,
,
①求证:直线AB恒过定点,并求出定点的坐标;
②当坐标原点O到直线AB的距离最大时,求直线AB的方程.
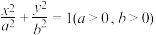 的长轴为双曲线
的长轴为双曲线 的实轴,且椭圆C过点
的实轴,且椭圆C过点 .
.(1)求椭圆C的标准方程;
(2)点A,B是椭圆C上异于点P的两个不同的点,直线PA与PB的斜率均存在,分别记为
 ,且
,且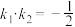 ,
,①求证:直线AB恒过定点,并求出定点的坐标;
②当坐标原点O到直线AB的距离最大时,求直线AB的方程.
您最近一年使用:0次
2022-09-23更新
|
810次组卷
|
3卷引用:河南省漯河市高级中学2021-2022学年高二下学期期中考试数学(文)试题
解题方法
8 . 已知椭圆 的离心率
的离心率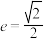 ,且过点
,且过点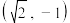 .
.
(1)求 的方程;
的方程;
(2)已知点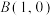 ,直线
,直线 与
与 交于
交于 、
、 两点,若
两点,若 的平分线垂直于
的平分线垂直于 轴,证明:
轴,证明: 过定点.
过定点.
 的离心率
的离心率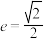 ,且过点
,且过点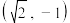 .
.(1)求
 的方程;
的方程;(2)已知点
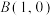 ,直线
,直线 与
与 交于
交于 、
、 两点,若
两点,若 的平分线垂直于
的平分线垂直于 轴,证明:
轴,证明: 过定点.
过定点.
您最近一年使用:0次
2022-06-20更新
|
666次组卷
|
5卷引用:河南省安阳市2021-2022学年高二下学期阶段性测试(五)文科数学试卷
河南省安阳市2021-2022学年高二下学期阶段性测试(五)文科数学试卷河南省安阳市2021-2022学年高二下学期阶段性测试(五)理科数学试卷(已下线)知识点:直线与圆锥曲线关系 易错点3 恒成立意义不明导致定点问题错误(已下线)突破3.1 椭圆(重难点突破)-【新教材优创】突破满分数学之2022-2023学年高二数学重难点突破+课时训练 (人教A版2019选择性必修第一册)(已下线)第25讲 圆锥曲线直线圆过定点问题
名校
解题方法
9 . 已知椭圆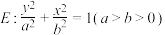 的焦距为
的焦距为 ,点
,点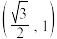 在椭圆
在椭圆 上.
上.
(1)求椭圆 的标准方程;
的标准方程;
(2)设直线 与椭圆
与椭圆 交于
交于 、
、 两点,
两点, 为坐标原点,求
为坐标原点,求 面积的取值范围.
面积的取值范围.
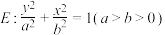 的焦距为
的焦距为 ,点
,点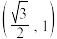 在椭圆
在椭圆 上.
上.(1)求椭圆
 的标准方程;
的标准方程;(2)设直线
 与椭圆
与椭圆 交于
交于 、
、 两点,
两点, 为坐标原点,求
为坐标原点,求 面积的取值范围.
面积的取值范围.
您最近一年使用:0次
2021-08-07更新
|
695次组卷
|
5卷引用:河南省郑州市第九中学2022-2023学年高二上学期期末数学试题
河南省郑州市第九中学2022-2023学年高二上学期期末数学试题陕西省安康市2020-2021学年高二下学期期末文科数学试题陕西省安康市2020-2021学年高二下学期期末理科数学试题(已下线)专题05 《圆锥曲线与方程》中的压轴题(1)-2021-2022学年高二数学同步培优训练系列(苏教版2019选择性必修第一册) 安徽省六安市皖西中学2021-2022学年高二上学期期末数学试题
解题方法
10 . 已知椭圆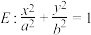 ,双曲线
,双曲线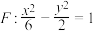 ,设椭圆
,设椭圆 与双曲线
与双曲线 有相同的焦点,点
有相同的焦点,点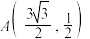 ,
,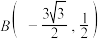 分别为椭圆
分别为椭圆 与双曲线
与双曲线 在第一、二象限的交点.
在第一、二象限的交点.
(1)求椭圆 的标准方程;
的标准方程;
(2)设直线 与
与 轴相交于点
轴相交于点 ,过点
,过点 作直线交椭圆
作直线交椭圆 于
于 ,
, 两点(不同于
两点(不同于 ,
, ),求证:直线
),求证:直线 与直线
与直线 的交点
的交点 在一定直线上运动,并求出该直线的方程.
在一定直线上运动,并求出该直线的方程.
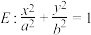 ,双曲线
,双曲线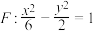 ,设椭圆
,设椭圆 与双曲线
与双曲线 有相同的焦点,点
有相同的焦点,点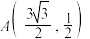 ,
,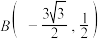 分别为椭圆
分别为椭圆 与双曲线
与双曲线 在第一、二象限的交点.
在第一、二象限的交点.(1)求椭圆
 的标准方程;
的标准方程;(2)设直线
 与
与 轴相交于点
轴相交于点 ,过点
,过点 作直线交椭圆
作直线交椭圆 于
于 ,
, 两点(不同于
两点(不同于 ,
, ),求证:直线
),求证:直线 与直线
与直线 的交点
的交点 在一定直线上运动,并求出该直线的方程.
在一定直线上运动,并求出该直线的方程.
您最近一年使用:0次
2021-08-04更新
|
805次组卷
|
5卷引用:河南省许昌市2020-2021学年高二下学期期末数学(理)试题
河南省许昌市2020-2021学年高二下学期期末数学(理)试题(已下线)第3章 圆锥曲线与方程 单元综合检测(能力提升)(单元培优)-2021-2022学年高二数学课后培优练(苏教版2019选择性必修第一册)(已下线)3.2 双曲线的标准方程-2021-2022学年高二数学同步培优训练系列(苏教版2019选择性必修第一册) 云南省昆明市第二十四中学2023届高三下学期教学质量第二次监测数学(理)试题(已下线)3.2 双曲线(练习)-高二数学同步精品课堂(苏教版2019选择性必修第一册)



