名校
解题方法
1 . 已知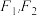 分别是椭圆
分别是椭圆 的左、右焦点,
的左、右焦点,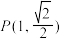 是椭圆
是椭圆 上一点,且
上一点,且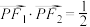 .
.
(1)求椭圆 的方程;
的方程;
(2)延长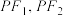 ,并与椭圆
,并与椭圆 分别相交于
分别相交于 两点,求
两点,求 的面积.
的面积.
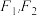 分别是椭圆
分别是椭圆 的左、右焦点,
的左、右焦点,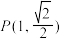 是椭圆
是椭圆 上一点,且
上一点,且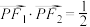 .
.(1)求椭圆
 的方程;
的方程;(2)延长
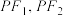 ,并与椭圆
,并与椭圆 分别相交于
分别相交于 两点,求
两点,求 的面积.
的面积.
您最近一年使用:0次
2023-08-21更新
|
1361次组卷
|
6卷引用:云南省昆明市第十中学2024届高三上学期开学考试数学试题
云南省昆明市第十中学2024届高三上学期开学考试数学试题黑龙江省大庆市2024届高三第一次教学质量检测数学试题(已下线)人教A版2019选择性必修第一册综合测试(提升)-2023-2024学年高二数学《一隅三反》系列(人教A版2019选择性必修第一册)(已下线)2.1.2 椭圆的简单几何性质(分层练习)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第一册)江苏省徐州市睢宁高级中学2023-2024学年高二上学期10月学情调研数学试题(已下线)模块一 专题2 解析几何(2)
名校
2 . 已知椭圆 的左焦点为
的左焦点为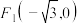 ,且点
,且点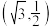 在椭圆C上.
在椭圆C上.
(1)求椭圆C的方程;
(2)已知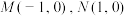 ,点P为椭圆C上一点.
,点P为椭圆C上一点.
(ⅰ)若点P在第一象限内,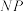 延长线交y轴于点Q,
延长线交y轴于点Q, 与
与 的面积之比为1∶2,求点P坐标;
的面积之比为1∶2,求点P坐标;
(ⅱ)设直线 与椭圆C的另一个交点为点B,直线
与椭圆C的另一个交点为点B,直线 与椭圆C的另一个交点为点D.设
与椭圆C的另一个交点为点D.设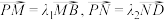 ,求证:当点P在椭圆C上运动时,
,求证:当点P在椭圆C上运动时, 为定值.
为定值.
 的左焦点为
的左焦点为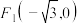 ,且点
,且点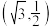 在椭圆C上.
在椭圆C上.(1)求椭圆C的方程;
(2)已知
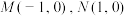 ,点P为椭圆C上一点.
,点P为椭圆C上一点.(ⅰ)若点P在第一象限内,
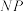 延长线交y轴于点Q,
延长线交y轴于点Q, 与
与 的面积之比为1∶2,求点P坐标;
的面积之比为1∶2,求点P坐标;(ⅱ)设直线
 与椭圆C的另一个交点为点B,直线
与椭圆C的另一个交点为点B,直线 与椭圆C的另一个交点为点D.设
与椭圆C的另一个交点为点D.设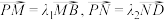 ,求证:当点P在椭圆C上运动时,
,求证:当点P在椭圆C上运动时, 为定值.
为定值.
您最近一年使用:0次
2024-08-26更新
|
684次组卷
|
3卷引用:云南省祥云县第一中学2024-2025学年高三上学期开学见面考数学试卷
云南省祥云县第一中学2024-2025学年高三上学期开学见面考数学试卷北京市海淀区首都师范大学附属中学2023-2024学年高三下学期5月三模数学试题(已下线)周测18 圆锥曲线(一轮好卷北京专版 )
名校
解题方法
3 . 知椭圆E: 的左右焦点分别为
的左右焦点分别为 ,
,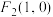 ,过
,过 且斜率为
且斜率为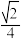 的直线与椭圆的一个交点在x轴上的射影恰好为
的直线与椭圆的一个交点在x轴上的射影恰好为
(1)求椭圆E的方程;
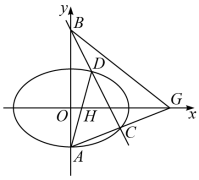
(2)如图,下顶点为A,过点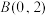 作一条与y轴不重合的直线.该直线交椭圆E于C,D两点.直线AD,AC分别交x轴于点H,
作一条与y轴不重合的直线.该直线交椭圆E于C,D两点.直线AD,AC分别交x轴于点H,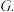 求证:
求证: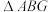 与
与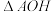 的面积之积为定值,并求出该定值.
的面积之积为定值,并求出该定值.
 的左右焦点分别为
的左右焦点分别为 ,
,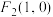 ,过
,过 且斜率为
且斜率为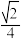 的直线与椭圆的一个交点在x轴上的射影恰好为
的直线与椭圆的一个交点在x轴上的射影恰好为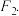

(1)求椭圆E的方程;
(2)如图,下顶点为A,过点
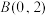 作一条与y轴不重合的直线.该直线交椭圆E于C,D两点.直线AD,AC分别交x轴于点H,
作一条与y轴不重合的直线.该直线交椭圆E于C,D两点.直线AD,AC分别交x轴于点H,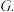 求证:
求证: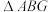 与
与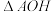 的面积之积为定值,并求出该定值.
的面积之积为定值,并求出该定值.
您最近一年使用:0次
2022-11-24更新
|
1163次组卷
|
19卷引用:云南省昆明市第一中学高中新课标2023届高三第一次摸底测试数学试题
云南省昆明市第一中学高中新课标2023届高三第一次摸底测试数学试题云南省曲靖市沾益区第四中学2020-2021学年高二5月月考数学(文)试题九师联盟2020-2021学年高三上学期12月联考(新高考)数学试题(已下线)黄金卷11 【赢在高考·黄金20卷】备战2021年高考数学全真模拟卷(广东专用)湖北省孝感高中2020-2021学年高三上学期12月联考数学试题(已下线)【新东方】高中数学20210527-014【2021】【高二下】山东省济南市历城第二中学2020-2021学年高三下学期检测数学试卷(一)(已下线)专题4 求面积运算(提升版)江西省临川第一中学2023届高三上学期期中考试数学(文)试题江苏省南京市建邺高中2022-2023学年高二上学期10月月考数学试题吉林省延边州2023届高三统考二模数学试题(已下线)专题09 平面解析几何(已下线)专题17 押全国卷(理科)第20题 圆锥曲线(已下线)第26讲 圆锥曲线中定值问题(1)(已下线)专题3.16 圆锥曲线中的定点、定值、定直线问题大题专项训练(30道)-2022-2023学年高二数学举一反三系列(人教A版2019选择性必修第一册)天津市武清区杨村第一中学2023届高三下学期第二次热身练数学试题江苏省苏南名校2023-2024学年高三上学期9月抽查调研数学试题(已下线)高二上学期期末【压轴60题考点专练】(选修一+选修二)湖南省衡阳市衡阳县第一中学2024届高三上学期11月月考数学试题
名校
解题方法
4 . 已知椭圆 的离心率为
的离心率为 ,且过点
,且过点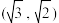 .
.
(1)求椭圆C的方程;
(2)若椭圆C的上顶点为P,过P的两条直线 ,
, 分别与C交于异于点P的A,B两点,若直线
分别与C交于异于点P的A,B两点,若直线 ,
, 的斜率之和为
的斜率之和为 ,试判断直线
,试判断直线 是否过定点?若是,求出该定点;若不是,请说明理由.
是否过定点?若是,求出该定点;若不是,请说明理由.
 的离心率为
的离心率为 ,且过点
,且过点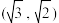 .
.(1)求椭圆C的方程;
(2)若椭圆C的上顶点为P,过P的两条直线
 ,
, 分别与C交于异于点P的A,B两点,若直线
分别与C交于异于点P的A,B两点,若直线 ,
, 的斜率之和为
的斜率之和为 ,试判断直线
,试判断直线 是否过定点?若是,求出该定点;若不是,请说明理由.
是否过定点?若是,求出该定点;若不是,请说明理由.
您最近一年使用:0次
2023-11-09更新
|
557次组卷
|
4卷引用:云南省昭通市水富市第一中学等三校联考2023-2024学年高二下学期开学考试数学试卷
名校
解题方法
5 . 已知椭圆E: 离心率为
离心率为 ,且经过点
,且经过点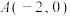 .
.
(1)求椭圆E的方程;
(2)过点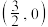 且斜率不为0的直线
且斜率不为0的直线 与椭圆C交于M,N两点,证明:直线
与椭圆C交于M,N两点,证明:直线 与直线
与直线 的斜率之积为定值.
的斜率之积为定值.
 离心率为
离心率为 ,且经过点
,且经过点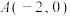 .
.(1)求椭圆E的方程;
(2)过点
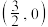 且斜率不为0的直线
且斜率不为0的直线 与椭圆C交于M,N两点,证明:直线
与椭圆C交于M,N两点,证明:直线 与直线
与直线 的斜率之积为定值.
的斜率之积为定值.
您最近一年使用:0次
2024-01-13更新
|
493次组卷
|
2卷引用:云南省开远市第一中学校2023-2024学年高二下学期开学考试数学试题
名校
解题方法
6 . 如图所示,已知椭圆 :
: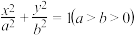 的离心率为
的离心率为 ,且过点
,且过点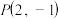 ,
,
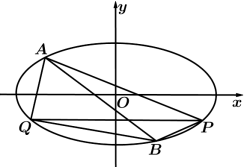
(1)求椭圆 的方程;
的方程;
(2)设 在椭圆
在椭圆 上,且
上,且 与
与 轴平行,过
轴平行,过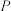 作两条直线分别交椭圆
作两条直线分别交椭圆 于两点
于两点 ,
, ,直线
,直线 平分
平分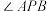 ,且直线
,且直线 过点
过点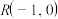 ,求四边形
,求四边形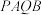 的面积.
的面积.
 :
: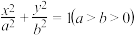 的离心率为
的离心率为 ,且过点
,且过点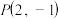 ,
,
(1)求椭圆
 的方程;
的方程;(2)设
 在椭圆
在椭圆 上,且
上,且 与
与 轴平行,过
轴平行,过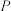 作两条直线分别交椭圆
作两条直线分别交椭圆 于两点
于两点 ,
, ,直线
,直线 平分
平分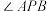 ,且直线
,且直线 过点
过点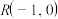 ,求四边形
,求四边形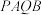 的面积.
的面积.
您最近一年使用:0次
2021-06-08更新
|
1444次组卷
|
5卷引用:云南省会泽县实验高级中学校2021-2022学年高二下学期开学考试数学试题
云南省会泽县实验高级中学校2021-2022学年高二下学期开学考试数学试题江苏省南京师范大学《数学之友》2021届高三下学期一模数学试题河北省衡水中学2022届高三上学期六调数学试题(已下线)查补易混易错点06 解析几何-【查漏补缺】2022年高考数学三轮冲刺过关(新高考专用)江苏省常州市华罗庚中学2022届高三下学期3月模拟数学试题
7 . 已知椭圆 (
( )的离心率为
)的离心率为 ,且过点
,且过点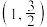 .
.
(1)求椭圆的标准方程
(2)分别过椭圆的左、右焦点 、
、 作两条互相垂直的直线
作两条互相垂直的直线 和
和 ,
, 与
与 交于
交于 ,
, 与椭圆交于A,B两点,
与椭圆交于A,B两点, 与椭圆交于C,D两点
与椭圆交于C,D两点
①求证: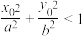 ;
;
②求证: 定值.
定值.
 (
( )的离心率为
)的离心率为 ,且过点
,且过点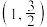 .
.(1)求椭圆的标准方程
(2)分别过椭圆的左、右焦点
 、
、 作两条互相垂直的直线
作两条互相垂直的直线 和
和 ,
, 与
与 交于
交于 ,
, 与椭圆交于A,B两点,
与椭圆交于A,B两点, 与椭圆交于C,D两点
与椭圆交于C,D两点①求证:
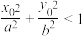 ;
;②求证:
 定值.
定值.
您最近一年使用:0次
2021-11-23更新
|
742次组卷
|
3卷引用:云南省玉溪第一中学2023-2024学年高二下学期开学考试数学试卷
云南省玉溪第一中学2023-2024学年高二下学期开学考试数学试卷山东省济南市历下区山东师范大学附属中学2021-2022学年高二上学期期中数学试题(已下线)专题44 直线与圆锥曲线的位置关系之定值、定点、共线问题-备战2022年高考数学一轮复习一网打尽之重点难点突破



