解题方法
1 . 观察椭圆 的形状,你能从图上看出它的范围吗?它具有怎样的对称性?椭圆上哪些点比较特殊?
的形状,你能从图上看出它的范围吗?它具有怎样的对称性?椭圆上哪些点比较特殊?
 的形状,你能从图上看出它的范围吗?它具有怎样的对称性?椭圆上哪些点比较特殊?
的形状,你能从图上看出它的范围吗?它具有怎样的对称性?椭圆上哪些点比较特殊?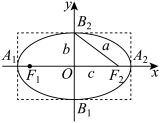
您最近一年使用:0次
名校
解题方法
2 . 已知椭圆C: 经过点
经过点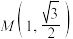 ,
, 、
、 是椭圆C的左、右两个焦点,
是椭圆C的左、右两个焦点, ,P是椭圆C上的一个动点.
,P是椭圆C上的一个动点.
(1)求椭圆C的标准方程;
(2)若点P在第一象限,且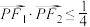 ,求点P的横坐标的取值范围.
,求点P的横坐标的取值范围.
 经过点
经过点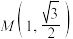 ,
, 、
、 是椭圆C的左、右两个焦点,
是椭圆C的左、右两个焦点, ,P是椭圆C上的一个动点.
,P是椭圆C上的一个动点.(1)求椭圆C的标准方程;
(2)若点P在第一象限,且
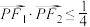 ,求点P的横坐标的取值范围.
,求点P的横坐标的取值范围.
您最近一年使用:0次
2024-07-15更新
|
649次组卷
|
2卷引用:【课后练】2.2.2.1 椭圆的性质 课后作业-沪教版(2020)选择性必修第一册第2章 圆锥曲线
3 . 椭圆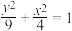 中,x,y的范围是什么?
中,x,y的范围是什么?
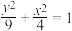 中,x,y的范围是什么?
中,x,y的范围是什么?
您最近一年使用:0次
解题方法
4 . 已知曲线 :
:
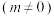 .
.
(1)若 为椭圆,点
为椭圆,点 是
是 的一个焦点,点
的一个焦点,点 是
是 上任意一点且
上任意一点且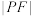 的最小值为2,求
的最小值为2,求 ;
;
(2)已知点 ,
, 是
是 上关于原点对称的两点,点
上关于原点对称的两点,点 是
是 上与
上与 ,
, 不重合的点.在下面两个条件中选一个,判断是否存在过点
不重合的点.在下面两个条件中选一个,判断是否存在过点 的直线与
的直线与 交于点
交于点 ,
, ,且线段
,且线段 的中点为
的中点为 ,若存在,求出直线
,若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
①直线 的斜率之积为2;②直线
的斜率之积为2;②直线 ,
,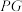 的斜率之积为
的斜率之积为 .
.
注:若选择多个条件分别解答,按第一个解答计分.
 :
:
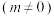 .
.(1)若
 为椭圆,点
为椭圆,点 是
是 的一个焦点,点
的一个焦点,点 是
是 上任意一点且
上任意一点且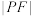 的最小值为2,求
的最小值为2,求 ;
;(2)已知点
 ,
, 是
是 上关于原点对称的两点,点
上关于原点对称的两点,点 是
是 上与
上与 ,
, 不重合的点.在下面两个条件中选一个,判断是否存在过点
不重合的点.在下面两个条件中选一个,判断是否存在过点 的直线与
的直线与 交于点
交于点 ,
, ,且线段
,且线段 的中点为
的中点为 ,若存在,求出直线
,若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.①直线
 的斜率之积为2;②直线
的斜率之积为2;②直线 ,
,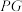 的斜率之积为
的斜率之积为 .
.注:若选择多个条件分别解答,按第一个解答计分.
您最近一年使用:0次
2023高三·全国·专题练习
名校
5 . 已知F1,F2分别为椭圆W: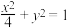 的左、右焦点,M为椭圆W上的一点.
的左、右焦点,M为椭圆W上的一点.
(1)若点M的坐标为(1,m)(m>0),求△F1MF2的面积;
(2)若点M的坐标为(x0,y0),且∠F1MF2是钝角,求横坐标x0的范围.
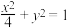 的左、右焦点,M为椭圆W上的一点.
的左、右焦点,M为椭圆W上的一点.(1)若点M的坐标为(1,m)(m>0),求△F1MF2的面积;
(2)若点M的坐标为(x0,y0),且∠F1MF2是钝角,求横坐标x0的范围.
您最近一年使用:0次
2023-10-10更新
|
1139次组卷
|
5卷引用:湖北省荆州中学2023-2024学年高二上学期10月月考数学试题
湖北省荆州中学2023-2024学年高二上学期10月月考数学试题(已下线)第三章 圆锥曲线的方程(知识归纳+题型突破)-2023-2024学年高二数学单元速记·巧练(人教A版2019选择性必修第一册)(已下线)第五节 椭圆 第一课时 椭圆的定义、方程与性质 B素养提升卷(已下线)考点12 圆锥曲线的几何性质(椭圆,双曲线,抛物线) 2024届高考数学考点总动员【练】广东省湛江市2023-2024学年高二下学期期末调研考试数学试卷
名校
6 . 已知椭圆E: 过点
过点 ,且左,右焦点分别为
,且左,右焦点分别为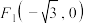 ,
,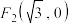 ,直线y=kx与椭圆交于A,B两点.
,直线y=kx与椭圆交于A,B两点.
(1)求椭圆E的方程;
(2)若椭圆上一动点 ,使得
,使得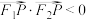 ,求点P的横坐标x的取值范围.
,求点P的横坐标x的取值范围.
(3)设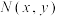 为椭圆上一点,且直线NA的斜率
为椭圆上一点,且直线NA的斜率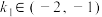 ,试求直线NB的斜率
,试求直线NB的斜率 的取值范围.
的取值范围.
 过点
过点 ,且左,右焦点分别为
,且左,右焦点分别为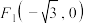 ,
,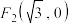 ,直线y=kx与椭圆交于A,B两点.
,直线y=kx与椭圆交于A,B两点.(1)求椭圆E的方程;
(2)若椭圆上一动点
 ,使得
,使得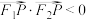 ,求点P的横坐标x的取值范围.
,求点P的横坐标x的取值范围.(3)设
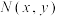 为椭圆上一点,且直线NA的斜率
为椭圆上一点,且直线NA的斜率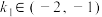 ,试求直线NB的斜率
,试求直线NB的斜率 的取值范围.
的取值范围.
您最近一年使用:0次
2023-07-03更新
|
378次组卷
|
3卷引用: 2.1.1椭圆及其标准方程 练习-2022-2023学年高二上学期数学北师大版(2019)选择性必修第一册
名校
解题方法
7 . 已知椭圆 ,四点
,四点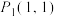 ,
, ,
, ,
, 中恰有三点在椭圆
中恰有三点在椭圆 上.
上.
(1)求 的方程;
的方程;
(2)设点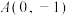 ,点
,点 是椭圆
是椭圆 上任意一点,求
上任意一点,求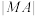 的最大值.
的最大值.
 ,四点
,四点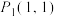 ,
, ,
, ,
, 中恰有三点在椭圆
中恰有三点在椭圆 上.
上.(1)求
 的方程;
的方程;(2)设点
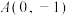 ,点
,点 是椭圆
是椭圆 上任意一点,求
上任意一点,求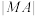 的最大值.
的最大值.
您最近一年使用:0次
2022-11-18更新
|
895次组卷
|
4卷引用:辽宁省阜蒙县育才高级中学2022-2023学年高二上学期期末考试数学试题
解题方法
8 . 已知椭圆C的离心率为 ,焦点
,焦点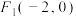 、
、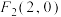 .
.
(1)求椭圆C的方程;
(2)已知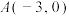 、
、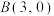 ,
,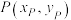 是椭圆C在第一象限部分上的一动点,且∠APB是钝角,求
是椭圆C在第一象限部分上的一动点,且∠APB是钝角,求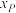 的取值范围.
的取值范围.
 ,焦点
,焦点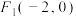 、
、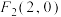 .
.(1)求椭圆C的方程;
(2)已知
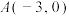 、
、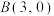 ,
,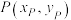 是椭圆C在第一象限部分上的一动点,且∠APB是钝角,求
是椭圆C在第一象限部分上的一动点,且∠APB是钝角,求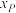 的取值范围.
的取值范围.
您最近一年使用:0次
21-22高二·全国·课后作业
9 . 已知点A,B是椭圆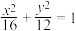 上不关于长轴对称的两点,且A,B两点到点
上不关于长轴对称的两点,且A,B两点到点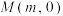 的距离相等,求实数m的取值范围.
的距离相等,求实数m的取值范围.
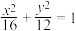 上不关于长轴对称的两点,且A,B两点到点
上不关于长轴对称的两点,且A,B两点到点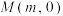 的距离相等,求实数m的取值范围.
的距离相等,求实数m的取值范围.
您最近一年使用:0次
2022-03-06更新
|
786次组卷
|
5卷引用:复习题二1
(已下线)复习题二1椭圆的几何性质(已下线)第20讲 椭圆的简单几何性质10种常见考法归类(2)北师大版(2019)选择性必修第一册课本习题第二章复习题广西壮族自治区钦州市第四中学2022-2023学年高二上学期10月月考数学试题
21-22高二·全国·课后作业
10 . 证明:以椭圆C: (
( )的焦点F为圆心的圆与该椭圆最多有两个公共点.
)的焦点F为圆心的圆与该椭圆最多有两个公共点.
 (
( )的焦点F为圆心的圆与该椭圆最多有两个公共点.
)的焦点F为圆心的圆与该椭圆最多有两个公共点.
您最近一年使用:0次
2022-03-06更新
|
208次组卷
|
3卷引用:复习题二1



