名校
1 . 过双曲线 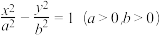 的左焦点
的左焦点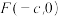 作圆x²+y²=a²的切线,切点为E,延长FE交抛物线y²=4cx于点P,O为坐标原点,若
作圆x²+y²=a²的切线,切点为E,延长FE交抛物线y²=4cx于点P,O为坐标原点,若 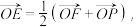 则双曲线的离心率为
则双曲线的离心率为_______ .
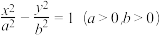 的左焦点
的左焦点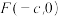 作圆x²+y²=a²的切线,切点为E,延长FE交抛物线y²=4cx于点P,O为坐标原点,若
作圆x²+y²=a²的切线,切点为E,延长FE交抛物线y²=4cx于点P,O为坐标原点,若 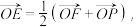 则双曲线的离心率为
则双曲线的离心率为
您最近一年使用:0次
2022-11-19更新
|
493次组卷
|
16卷引用:上海市杨浦区复旦大学附属中学2022-2023学年高二上学期期中数学试题
上海市杨浦区复旦大学附属中学2022-2023学年高二上学期期中数学试题【巩固卷】期中测评卷 单元测试A-沪教版(2020)选择性必修第一册2015-2016学年江西省高安中学高二上期中文科数学试卷2015-2016学年江西高安中学高二重点上期中文数学卷2015-2016学年江西省南昌市八一中学等高二上学期期中文科数学试卷2016届重庆市巴蜀中学高三10月月考理科数学试卷2017届安徽六安一中高三上学期开学考试数学(文)试卷2016-2017学年安徽寿县一中高二文上月考二数学试卷2020届四川省绵阳南山中学高三上学期12月月考 数学(理)试题湖北省武汉一中2021届高三下学期二模数学试题(已下线)专题11 圆锥曲线的方程综合练习-(新教材)2020-2021学年高二数学单元复习(人教A版选择性必修第一册)福建省福州第八中学2022-2023学年高二上学期期末考试数学试题湖北省襄阳市第四中学2022-2023学年高二下学期开学考试数学试题四川省绵阳市三台中学校2024届高三上学期第四次月考数学(理)试题湖北省恩施州巴东县第一高级中学2023-2024学年高二上学期第五次月考数学试题福建省福州市城门中学2023-2024学年高二上学期期末温习模拟数学试题
解题方法
2 . 已知双曲线 .
.
(1)若离心率为 ,求b的值,
,求b的值, 的顶点坐标、渐近线方程;
的顶点坐标、渐近线方程;
(2)若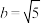 ,是否存在被点
,是否存在被点 平分的弦?如果存在,求弦所在的直线方程;如不存在,请说明理由.
平分的弦?如果存在,求弦所在的直线方程;如不存在,请说明理由.
 .
.(1)若离心率为
 ,求b的值,
,求b的值, 的顶点坐标、渐近线方程;
的顶点坐标、渐近线方程;(2)若
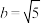 ,是否存在被点
,是否存在被点 平分的弦?如果存在,求弦所在的直线方程;如不存在,请说明理由.
平分的弦?如果存在,求弦所在的直线方程;如不存在,请说明理由.
您最近一年使用:0次
2022-04-26更新
|
471次组卷
|
3卷引用:上海市华东师范大学附属东昌中学2021-2022学年高二下学期期中数学试题
上海市华东师范大学附属东昌中学2021-2022学年高二下学期期中数学试题(已下线)2.3双曲线(作业)(夯实基础+能力提升)-【教材配套课件+作业】2022-2023学年高二数学精品教学课件(沪教版2020选修第一册)【随堂练】2.3.2.1 双曲线的性质 随堂练习-沪教版(2020)选择性必修第一册第2章 圆锥曲线
名校
解题方法
3 . 过双曲线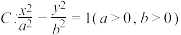 右焦点
右焦点 作直线
作直线 ,且直线
,且直线 与双曲线
与双曲线 的一条渐近线垂直,垂足为
的一条渐近线垂直,垂足为 ,直线
,直线 与另一条渐近线交于点
与另一条渐近线交于点 .已知
.已知 为坐标原点,若
为坐标原点,若 的内切圆的半径为
的内切圆的半径为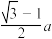 ,则双曲线
,则双曲线 的离心率为
的离心率为_________ .
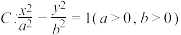 右焦点
右焦点 作直线
作直线 ,且直线
,且直线 与双曲线
与双曲线 的一条渐近线垂直,垂足为
的一条渐近线垂直,垂足为 ,直线
,直线 与另一条渐近线交于点
与另一条渐近线交于点 .已知
.已知 为坐标原点,若
为坐标原点,若 的内切圆的半径为
的内切圆的半径为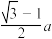 ,则双曲线
,则双曲线 的离心率为
的离心率为
您最近一年使用:0次
2021-11-14更新
|
899次组卷
|
10卷引用:上海市大同中学2021-2022学年高二下学期期中数学试题
上海市大同中学2021-2022学年高二下学期期中数学试题(已下线)专题9.8 《平面解析几何》单元测试卷 2022年高考数学一轮复习讲练测(新教材新高考)(已下线)考点39 双曲线-备战2022年高考数学典型试题解读与变式(已下线)核心考点03椭圆与双曲线(2)宁夏银川市第二中学2023-2024学年高二上学期期中考试数学试题广东省东莞市东莞中学松山湖学校2023-2024学年高二上学期第二次段考(期中)数学试题(已下线)数学(上海卷02)山西省山西大学附属中学2022届高三上学期10月模块诊断数学(理)试题福建省莆田第二中学2021-2022学年高二12月阶段性检测数学试题(已下线)思想01 运用分类讨论的思想方法解题(精讲精练)-1
名校
4 . 设 是双曲线
是双曲线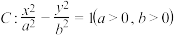 的左、右焦点.
的左、右焦点. 是坐标原点.过
是坐标原点.过 作
作 的一条渐近线的垂线,垂足为
的一条渐近线的垂线,垂足为 ,若
,若 ,则
,则 的离心率为
的离心率为_______________________ .
 是双曲线
是双曲线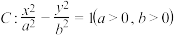 的左、右焦点.
的左、右焦点. 是坐标原点.过
是坐标原点.过 作
作 的一条渐近线的垂线,垂足为
的一条渐近线的垂线,垂足为 ,若
,若 ,则
,则 的离心率为
的离心率为
您最近一年使用:0次
2021-01-16更新
|
235次组卷
|
2卷引用:上海市格致中学2023届高三上学期期中数学试题
2014·全国·一模
名校
解题方法
5 . 已知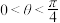 ,则双曲线
,则双曲线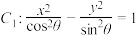 与
与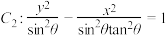 的 ( )
的 ( )
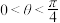 ,则双曲线
,则双曲线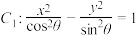 与
与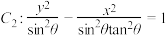 的 ( )
的 ( )| A.实轴长相等 | B.虚轴长相等 | C.焦距相等 | D.离心率相等 |
您最近一年使用:0次
2018-03-22更新
|
910次组卷
|
6卷引用:上海市杨浦区复旦大学附属中学2022-2023学年高二上学期期中数学试题
上海市杨浦区复旦大学附属中学2022-2023学年高二上学期期中数学试题(已下线)2014高考名师推荐数学理科双曲线2016-2017学年河北唐山一中高二10月月考数学试卷安徽省六安市舒城中学2017-2018学年高二下学期第一次统考(开学考试)数学(文)试题(已下线)秒杀题型01 圆锥曲线方程-2020年高考数学试题调研之秒杀圆锥曲线压轴题(已下线)专题27 双曲线-十年(2011-2020)高考真题数学分项



