1 . 椭圆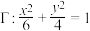 ,过椭圆
,过椭圆 外一点
外一点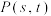 作椭圆
作椭圆 的两条切线
的两条切线 ,切点分别为
,切点分别为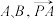 和
和 的夹角为
的夹角为 .
.
(1)若 ,求此时
,求此时 的值;
的值;
(2)若 ,求证:
,求证: 随
随 的增大而减小;
的增大而减小;
(3)是否存在圆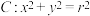 ,使得
,使得 在其上做圆周运动时,始终可以保持
在其上做圆周运动时,始终可以保持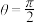 ?不论存在与否,均请说明理由.
?不论存在与否,均请说明理由.
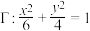 ,过椭圆
,过椭圆 外一点
外一点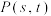 作椭圆
作椭圆 的两条切线
的两条切线 ,切点分别为
,切点分别为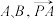 和
和 的夹角为
的夹角为 .
.(1)若
 ,求此时
,求此时 的值;
的值;(2)若
 ,求证:
,求证: 随
随 的增大而减小;
的增大而减小;(3)是否存在圆
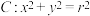 ,使得
,使得 在其上做圆周运动时,始终可以保持
在其上做圆周运动时,始终可以保持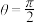 ?不论存在与否,均请说明理由.
?不论存在与否,均请说明理由.
您最近一年使用:0次
名校
解题方法
2 . 设常数 且
且 ,椭圆
,椭圆 :
: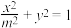 ,点
,点 是
是 上的动点.
上的动点.
(1)若点 的坐标为
的坐标为 ,求
,求 的焦点坐标;
的焦点坐标;
(2)设 ,若定点
,若定点 的坐标为
的坐标为 ,求
,求 的最大值与最小值;
的最大值与最小值;
(3)设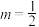 ,若
,若 上的另一动点
上的另一动点 满足
满足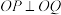 (
( 为坐标原点),求证:
为坐标原点),求证: 到直线PQ的距离是定值.
到直线PQ的距离是定值.
 且
且 ,椭圆
,椭圆 :
: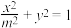 ,点
,点 是
是 上的动点.
上的动点.(1)若点
 的坐标为
的坐标为 ,求
,求 的焦点坐标;
的焦点坐标;(2)设
 ,若定点
,若定点 的坐标为
的坐标为 ,求
,求 的最大值与最小值;
的最大值与最小值;(3)设
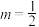 ,若
,若 上的另一动点
上的另一动点 满足
满足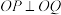 (
( 为坐标原点),求证:
为坐标原点),求证: 到直线PQ的距离是定值.
到直线PQ的距离是定值.
您最近一年使用:0次
2021-12-23更新
|
1026次组卷
|
7卷引用:上海市嘉定区第二中学2022-2023学年高二上学期期中数学试题
上海市嘉定区第二中学2022-2023学年高二上学期期中数学试题上海市黄浦区2022届高三一模数学试题(已下线)上海市黄浦区2022届高三上学期一模数学试题(已下线)专题10.3—圆锥曲线—椭圆大题(定值问题)—2022届高三数学一轮复习精讲精练上海市崇明中学2021-2022学年高二下学期期中数学试题(已下线)押全国卷(理科)第20题 圆锥曲线-备战2022年高考数学(理)临考题号押题(全国卷)上海市格致中学2023-2024学年高二下学期期末考数学试卷
名校
解题方法
3 . 为了监测某海域的船舶航行情况,海事部门在该海域,设立了如图所示东西走向,相距 海里的
海里的 ,
, 两个观测站,观测范围是到
两个观测站,观测范围是到 ,
, 两观测站距离之和不超过
两观测站距离之和不超过 海里的区域.
海里的区域.
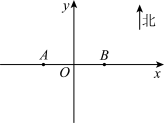
(1)以 所在直线为
所在直线为 轴,线段
轴,线段 的垂直平分线为
的垂直平分线为 轴建立平面直角坐标系,求观测区域边界曲线的方程;
轴建立平面直角坐标系,求观测区域边界曲线的方程;
(2)某日上午7时,观测站B发现在其正东10海里的C处,有一艘轮船正以每小时8海里的速度向北偏西45°方向航行,问该轮船大约在什么时间离开观测区域?(精确到1小时).
 海里的
海里的 ,
, 两个观测站,观测范围是到
两个观测站,观测范围是到 ,
, 两观测站距离之和不超过
两观测站距离之和不超过 海里的区域.
海里的区域.
(1)以
 所在直线为
所在直线为 轴,线段
轴,线段 的垂直平分线为
的垂直平分线为 轴建立平面直角坐标系,求观测区域边界曲线的方程;
轴建立平面直角坐标系,求观测区域边界曲线的方程;(2)某日上午7时,观测站B发现在其正东10海里的C处,有一艘轮船正以每小时8海里的速度向北偏西45°方向航行,问该轮船大约在什么时间离开观测区域?(精确到1小时).
您最近一年使用:0次
2021-08-16更新
|
354次组卷
|
2卷引用:上海市嘉定区第一中学2021届高三下学期3月月考数学试题



