名校
解题方法
1 . 已知 ,直线
,直线 为平面内的一个动点,过点
为平面内的一个动点,过点 作
作 的垂线,垂足为
的垂线,垂足为 ,且
,且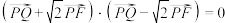 ,动点
,动点 的轨迹记为曲线
的轨迹记为曲线 .
.
(1)求 的方程;
的方程;
(2)若直线 交
交 于
于 两点,交圆
两点,交圆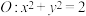 于
于 两点,且
两点,且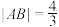 ,当
,当 的面积最大时,求
的面积最大时,求 的倾斜角.
的倾斜角.
 ,直线
,直线 为平面内的一个动点,过点
为平面内的一个动点,过点 作
作 的垂线,垂足为
的垂线,垂足为 ,且
,且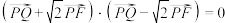 ,动点
,动点 的轨迹记为曲线
的轨迹记为曲线 .
.(1)求
 的方程;
的方程;(2)若直线
 交
交 于
于 两点,交圆
两点,交圆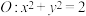 于
于 两点,且
两点,且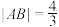 ,当
,当 的面积最大时,求
的面积最大时,求 的倾斜角.
的倾斜角.
您最近一年使用:0次
7日内更新
|
52次组卷
|
2卷引用:河北省南宫市私立丰翼中学2023-2024学年高二下学期第三次月考(5月)数学试卷
2 . 已知椭圆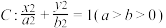 的左、右焦点分别为
的左、右焦点分别为 ,
, ,离心率为
,离心率为 ,点
,点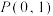 ,且
,且 为等腰直角三角形.
为等腰直角三角形.
(1)求椭圆 的标准方程;
的标准方程;
(2)设点 为
为 上的一个动点,求
上的一个动点,求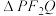 面积的最大值;
面积的最大值;
(3)若直线 与
与 交于
交于 两点,且
两点,且 ,证明:直线
,证明:直线 过定点.
过定点.
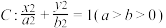 的左、右焦点分别为
的左、右焦点分别为 ,
, ,离心率为
,离心率为 ,点
,点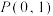 ,且
,且 为等腰直角三角形.
为等腰直角三角形.(1)求椭圆
 的标准方程;
的标准方程;(2)设点
 为
为 上的一个动点,求
上的一个动点,求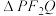 面积的最大值;
面积的最大值;(3)若直线
 与
与 交于
交于 两点,且
两点,且 ,证明:直线
,证明:直线 过定点.
过定点.
您最近一年使用:0次
7日内更新
|
135次组卷
|
2卷引用:河南省部分重点高中(金科未来)2023-2024学年高二下学期5月大联考数学试题
解题方法
3 . 已知椭圆 的离心率为
的离心率为 ;直线
;直线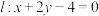 与
与 只有一个交点.
只有一个交点.
(1)求 的方程;
的方程;
(2) 的左、右焦点分别为
的左、右焦点分别为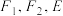 上的点
上的点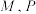 (
(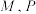 两点在
两点在 轴上方)满足
轴上方)满足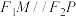 .
.
①试判断 (
( 为原点)是否成立,并说明理由;
为原点)是否成立,并说明理由;
②求四边形 面积的最大值.
面积的最大值.
 的离心率为
的离心率为 ;直线
;直线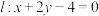 与
与 只有一个交点.
只有一个交点.(1)求
 的方程;
的方程;(2)
 的左、右焦点分别为
的左、右焦点分别为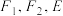 上的点
上的点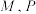 (
(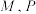 两点在
两点在 轴上方)满足
轴上方)满足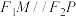 .
.①试判断
 (
( 为原点)是否成立,并说明理由;
为原点)是否成立,并说明理由;②求四边形
 面积的最大值.
面积的最大值.
您最近一年使用:0次
解题方法
4 . 已知椭圆 的左、右焦点分别为
的左、右焦点分别为 ,点
,点 是其左、右顶点,点
是其左、右顶点,点 为
为 上异于
上异于 的点,满足直线
的点,满足直线 与
与 的斜率之积为
的斜率之积为 的周长为6.
的周长为6.
(1)求椭圆 的方程;
的方程;
(2)直线 过点
过点 ,与椭圆
,与椭圆 交于
交于 两点,当
两点,当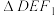 外接圆面积最小时,求直线
外接圆面积最小时,求直线 的方程.
的方程.
 的左、右焦点分别为
的左、右焦点分别为 ,点
,点 是其左、右顶点,点
是其左、右顶点,点 为
为 上异于
上异于 的点,满足直线
的点,满足直线 与
与 的斜率之积为
的斜率之积为 的周长为6.
的周长为6.(1)求椭圆
 的方程;
的方程;(2)直线
 过点
过点 ,与椭圆
,与椭圆 交于
交于 两点,当
两点,当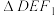 外接圆面积最小时,求直线
外接圆面积最小时,求直线 的方程.
的方程.
您最近一年使用:0次
解题方法
5 . 已知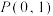 在椭圆
在椭圆 :
: 上,
上, 的左焦点
的左焦点 在抛物线
在抛物线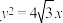 的准线上,
的准线上, 为
为 的左顶点,直线
的左顶点,直线 ,
, 分别与
分别与 另交于
另交于 ,
, 两点,直线
两点,直线 ,
, 的斜率之积为
的斜率之积为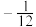 .
.
(1)求 的方程;
的方程;
(2)求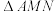 面积的最大值.
面积的最大值.
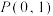 在椭圆
在椭圆 :
: 上,
上, 的左焦点
的左焦点 在抛物线
在抛物线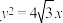 的准线上,
的准线上, 为
为 的左顶点,直线
的左顶点,直线 ,
, 分别与
分别与 另交于
另交于 ,
, 两点,直线
两点,直线 ,
, 的斜率之积为
的斜率之积为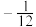 .
.(1)求
 的方程;
的方程;(2)求
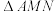 面积的最大值.
面积的最大值.
您最近一年使用:0次
解题方法
6 . 已知椭圆 :
: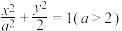 的离心率为
的离心率为 .
.
(1)求 的方程;
的方程;
(2)过 的右焦点
的右焦点 的直线
的直线 与
与 交于
交于 ,
, 两点,与直线
两点,与直线 交于点
交于点 ,且
,且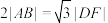 ,求
,求 的斜率.
的斜率.
 :
: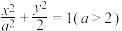 的离心率为
的离心率为 .
.(1)求
 的方程;
的方程;(2)过
 的右焦点
的右焦点 的直线
的直线 与
与 交于
交于 ,
, 两点,与直线
两点,与直线 交于点
交于点 ,且
,且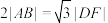 ,求
,求 的斜率.
的斜率.
您最近一年使用:0次
2024-05-20更新
|
398次组卷
|
3卷引用:青海省部分学校2023-2024学年高三下学期联考模拟预测理科数学试题
7 . 已知椭圆 的左、右焦点分别为
的左、右焦点分别为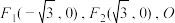 为坐标原点,直线
为坐标原点,直线 与
与 交于
交于 两点,点
两点,点 在第一象限,点
在第一象限,点 在第四象限且满足直线
在第四象限且满足直线 与直线
与直线 的斜率之积为
的斜率之积为 .当
.当 垂直于
垂直于 轴时,
轴时,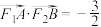 .
.
(1)求 的方程;
的方程;
(2)若点 为
为 的左顶点且满足
的左顶点且满足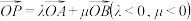 ,直线
,直线 与
与 交于
交于 ,直线
,直线 与
与 交于
交于 .
.
①证明: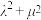 为定值;
为定值;
②证明:四边形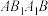 的面积是
的面积是 面积的2倍.
面积的2倍.
 的左、右焦点分别为
的左、右焦点分别为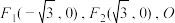 为坐标原点,直线
为坐标原点,直线 与
与 交于
交于 两点,点
两点,点 在第一象限,点
在第一象限,点 在第四象限且满足直线
在第四象限且满足直线 与直线
与直线 的斜率之积为
的斜率之积为 .当
.当 垂直于
垂直于 轴时,
轴时,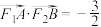 .
.(1)求
 的方程;
的方程;(2)若点
 为
为 的左顶点且满足
的左顶点且满足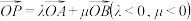 ,直线
,直线 与
与 交于
交于 ,直线
,直线 与
与 交于
交于 .
.①证明:
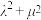 为定值;
为定值;②证明:四边形
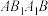 的面积是
的面积是 面积的2倍.
面积的2倍.
您最近一年使用:0次
8 . 已知A,B分别为椭圆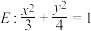 的上下顶点,P为直线
的上下顶点,P为直线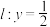 上的动点,且P不在椭圆上,
上的动点,且P不在椭圆上, 与椭圆E的另一交点为C,
与椭圆E的另一交点为C, 与椭圆E的另一交点为D,(C,D均不与椭圆E上下顶点重合).
与椭圆E的另一交点为D,(C,D均不与椭圆E上下顶点重合).
(1)证明:直线 过定点;
过定点;
(2)设(1)问中定点为Q,过点C,D分别作直线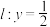 的垂线,垂足分别为M,N,记
的垂线,垂足分别为M,N,记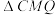 ,
,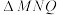 ,
,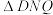 的面积分别为
的面积分别为 ,
, ,
, ,试问:是否存在常数t,使得
,试问:是否存在常数t,使得 ,
, ,
, 总为等比数列?若存在,求出t的值;若不存在,说明理由.
总为等比数列?若存在,求出t的值;若不存在,说明理由.
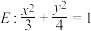 的上下顶点,P为直线
的上下顶点,P为直线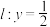 上的动点,且P不在椭圆上,
上的动点,且P不在椭圆上, 与椭圆E的另一交点为C,
与椭圆E的另一交点为C, 与椭圆E的另一交点为D,(C,D均不与椭圆E上下顶点重合).
与椭圆E的另一交点为D,(C,D均不与椭圆E上下顶点重合).(1)证明:直线
 过定点;
过定点;(2)设(1)问中定点为Q,过点C,D分别作直线
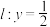 的垂线,垂足分别为M,N,记
的垂线,垂足分别为M,N,记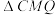 ,
,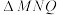 ,
,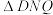 的面积分别为
的面积分别为 ,
, ,
, ,试问:是否存在常数t,使得
,试问:是否存在常数t,使得 ,
, ,
, 总为等比数列?若存在,求出t的值;若不存在,说明理由.
总为等比数列?若存在,求出t的值;若不存在,说明理由.
您最近一年使用:0次
9 . 已知椭圆 的离心率为
的离心率为 ,中心是坐标原点
,中心是坐标原点 ,焦点在
,焦点在 轴上,右焦点为F,A、B分别是
轴上,右焦点为F,A、B分别是 的上、下顶点.
的上、下顶点. 的短半轴长是圆
的短半轴长是圆 的半径,点
的半径,点 是圆
是圆 上的动点,且点
上的动点,且点 不在
不在 轴上,延长BM与
轴上,延长BM与 交于点
交于点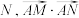 的取值范围为
的取值范围为 .
.
(1)求椭圆 、圆
、圆 的方程;
的方程;
(2)当直线BM经过点 时,求
时,求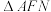 的面积;
的面积;
(3)记直线AM、AN的斜率分别为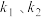 ,证明:
,证明: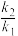 为定值.
为定值.
 的离心率为
的离心率为 ,中心是坐标原点
,中心是坐标原点 ,焦点在
,焦点在 轴上,右焦点为F,A、B分别是
轴上,右焦点为F,A、B分别是 的上、下顶点.
的上、下顶点. 的短半轴长是圆
的短半轴长是圆 的半径,点
的半径,点 是圆
是圆 上的动点,且点
上的动点,且点 不在
不在 轴上,延长BM与
轴上,延长BM与 交于点
交于点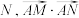 的取值范围为
的取值范围为 .
.(1)求椭圆
 、圆
、圆 的方程;
的方程;(2)当直线BM经过点
 时,求
时,求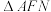 的面积;
的面积;(3)记直线AM、AN的斜率分别为
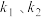 ,证明:
,证明: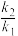 为定值.
为定值.
您最近一年使用:0次
解题方法
10 . 已知椭圆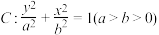 的离心率为
的离心率为 ,点
,点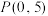 在椭圆
在椭圆 上,过点
上,过点 的直线
的直线 与椭圆
与椭圆 交于A,B两点,直线PA,PB与直线
交于A,B两点,直线PA,PB与直线 分别交于点M,N
分别交于点M,N
(1)求椭圆C的方程;
(2)若T为椭圆 的上焦点,求
的上焦点,求 面积取得最大值时直线
面积取得最大值时直线 的方程;
的方程;
(3)若 的外接圆经过原点
的外接圆经过原点 ,求
,求 的值.
的值.
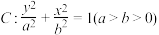 的离心率为
的离心率为 ,点
,点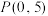 在椭圆
在椭圆 上,过点
上,过点 的直线
的直线 与椭圆
与椭圆 交于A,B两点,直线PA,PB与直线
交于A,B两点,直线PA,PB与直线 分别交于点M,N
分别交于点M,N(1)求椭圆C的方程;
(2)若T为椭圆
 的上焦点,求
的上焦点,求 面积取得最大值时直线
面积取得最大值时直线 的方程;
的方程;(3)若
 的外接圆经过原点
的外接圆经过原点 ,求
,求 的值.
的值.
您最近一年使用:0次



