解题方法
1 . 已知以坐标原点 为圆心的圆与抛物线
为圆心的圆与抛物线 :
: 相交于不同的两点
相交于不同的两点 ,与抛物线
,与抛物线 的准线相交于不同的两点
的准线相交于不同的两点 ,且
,且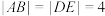 .
.
(1)求抛物线 的方程;
的方程;
(2)若不经过坐标原点 的直线
的直线 与抛物线
与抛物线 相交于不同的两点
相交于不同的两点 、
、 ,且满足
,且满足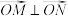 ,证明直线
,证明直线 过定点
过定点 ,并求出点
,并求出点 的坐标.
的坐标.
 为圆心的圆与抛物线
为圆心的圆与抛物线 :
: 相交于不同的两点
相交于不同的两点 ,与抛物线
,与抛物线 的准线相交于不同的两点
的准线相交于不同的两点 ,且
,且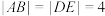 .
.(1)求抛物线
 的方程;
的方程;(2)若不经过坐标原点
 的直线
的直线 与抛物线
与抛物线 相交于不同的两点
相交于不同的两点 、
、 ,且满足
,且满足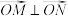 ,证明直线
,证明直线 过定点
过定点 ,并求出点
,并求出点 的坐标.
的坐标.
您最近一年使用:0次
2022-12-17更新
|
427次组卷
|
2卷引用:四川省成都市简阳市阳安中学2022-2023学年高二上学期12月月考数学(理)试题
名校
解题方法
2 . 设抛物线 的准线为l,A、B为抛物线上两动点,
的准线为l,A、B为抛物线上两动点,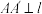 于
于 ,定点
,定点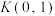 使
使 有最小值
有最小值 .
.
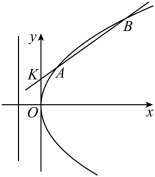
(1)求抛物线的方程;
(2)当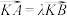 (
(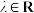 且
且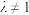 )时,是否存在一定点T满足
)时,是否存在一定点T满足 为定值?若存在,求出T的坐标和该定值;若不存在,请说明理由.
为定值?若存在,求出T的坐标和该定值;若不存在,请说明理由.
 的准线为l,A、B为抛物线上两动点,
的准线为l,A、B为抛物线上两动点,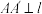 于
于 ,定点
,定点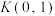 使
使 有最小值
有最小值 .
.
(1)求抛物线的方程;
(2)当
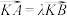 (
(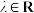 且
且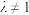 )时,是否存在一定点T满足
)时,是否存在一定点T满足 为定值?若存在,求出T的坐标和该定值;若不存在,请说明理由.
为定值?若存在,求出T的坐标和该定值;若不存在,请说明理由.
您最近一年使用:0次
2022-12-04更新
|
1675次组卷
|
10卷引用:四川省成都市第七中学2022-2023学年高二上学期期中数学理科试题
四川省成都市第七中学2022-2023学年高二上学期期中数学理科试题四川省成都市成都市第七中学2022-2023学年高二上学期期中数学文科试题四川省成都市树德中学2022-2023学年高二上学期期中考试数学(理)试题云南省大理市下关第一中学教育集团2022~2023学年高二上学期段考(二)数学试题(A卷)云南省下关第一中学2022-2023学年高二上学期段考(二)数学(A卷)试题辽宁省沈阳市东北育才双语学校2022-2023学年高二上学期期末数学试题(已下线)专题04 圆锥曲线经典题型全归纳(2)广西壮族自治区南宁市第三中学2023届高三模拟数学(理)试题(二)湖南省长沙市长郡中学2023-2024学年高二上学期期中数学试题(已下线)3.3.2 抛物线的简单几何性质【第三课】“上好三节课,做好三套题“高中数学素养晋级之路
名校
解题方法
3 . 已知抛物线 过点
过点 ,
, 为原点.
为原点.
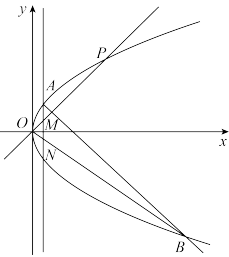
(1)求抛物线 的方程,并求其焦点坐标和准线方程;
的方程,并求其焦点坐标和准线方程;
(2)直线 与抛物线
与抛物线 交于不同的两点
交于不同的两点 、
、 (
( 、
、 不与
不与 重合).过点
重合).过点 作
作 轴的垂线分别与直线
轴的垂线分别与直线 、
、 交于点
交于点 、
、 ,且
,且 为线段
为线段 的中点.试判断直线
的中点.试判断直线 是否过定点?若是,求出该定点;若不是,说明理由.
是否过定点?若是,求出该定点;若不是,说明理由.
 过点
过点 ,
, 为原点.
为原点.
(1)求抛物线
 的方程,并求其焦点坐标和准线方程;
的方程,并求其焦点坐标和准线方程;(2)直线
 与抛物线
与抛物线 交于不同的两点
交于不同的两点 、
、 (
( 、
、 不与
不与 重合).过点
重合).过点 作
作 轴的垂线分别与直线
轴的垂线分别与直线 、
、 交于点
交于点 、
、 ,且
,且 为线段
为线段 的中点.试判断直线
的中点.试判断直线 是否过定点?若是,求出该定点;若不是,说明理由.
是否过定点?若是,求出该定点;若不是,说明理由.
您最近一年使用:0次
2022-11-28更新
|
467次组卷
|
2卷引用:四川省成都市树德中学2022-2023学年高二上学期11月阶段性测试数学试题
名校
解题方法
4 . 在平面直角坐标系xOy中,抛物线C的顶点是原点,以x轴为对称轴,且经过点 .
.
(1)求抛物线C的方程;
(2)已知直线 与抛物线C交于A,B两点,在抛物线C上是否存在点Q,使得直线QA,QB分别于y轴交于M,N两点,且
与抛物线C交于A,B两点,在抛物线C上是否存在点Q,使得直线QA,QB分别于y轴交于M,N两点,且 ,若存在,求点Q的坐标;若不存在,请说明理由.
,若存在,求点Q的坐标;若不存在,请说明理由.
 .
.(1)求抛物线C的方程;
(2)已知直线
 与抛物线C交于A,B两点,在抛物线C上是否存在点Q,使得直线QA,QB分别于y轴交于M,N两点,且
与抛物线C交于A,B两点,在抛物线C上是否存在点Q,使得直线QA,QB分别于y轴交于M,N两点,且 ,若存在,求点Q的坐标;若不存在,请说明理由.
,若存在,求点Q的坐标;若不存在,请说明理由.
您最近一年使用:0次
2022-10-11更新
|
412次组卷
|
3卷引用:四川省内江市第六中学2022-2023学年高三上学期入学考试数学(文科)试题
5 . 已知抛物线C: 的焦点为F,过点P(0,2)的动直线l与抛物线相交于A,B两点.当l经过点F时,点A恰好为线段PF中点.
的焦点为F,过点P(0,2)的动直线l与抛物线相交于A,B两点.当l经过点F时,点A恰好为线段PF中点.
(1)求p的值;
(2)是否存在定点T, 使得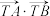 为常数? 若存在,求出点T的坐标及该常数; 若不存在,说明理由.
为常数? 若存在,求出点T的坐标及该常数; 若不存在,说明理由.
 的焦点为F,过点P(0,2)的动直线l与抛物线相交于A,B两点.当l经过点F时,点A恰好为线段PF中点.
的焦点为F,过点P(0,2)的动直线l与抛物线相交于A,B两点.当l经过点F时,点A恰好为线段PF中点.(1)求p的值;
(2)是否存在定点T, 使得
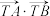 为常数? 若存在,求出点T的坐标及该常数; 若不存在,说明理由.
为常数? 若存在,求出点T的坐标及该常数; 若不存在,说明理由.
您最近一年使用:0次
2022-09-08更新
|
937次组卷
|
4卷引用:四川省成都外国语学校2022-2023学年高二上学期12月月考数学(文)试题
四川省成都外国语学校2022-2023学年高二上学期12月月考数学(文)试题四川省成都外国语学校2022-2023学年高二上学期12月月考数学(理)试题江苏省南京市2022-2023学年高三上学期9月学情调研数学试题(已下线)专题3.13 直线与抛物线的位置关系-重难点题型精讲-2022-2023学年高二数学举一反三系列(人教A版2019选择性必修第一册)
解题方法
6 . 抛物线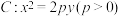 的焦点
的焦点 是椭圆
是椭圆 的一个焦点.
的一个焦点.
(1)求 的准线方程;
的准线方程;
(2)若 是直线
是直线 上的一动点,过
上的一动点,过 向
向 作两条切线,切点为M,N,试探究直线MN是否过定点?若是,请求出定点,若否,请说明理由.
作两条切线,切点为M,N,试探究直线MN是否过定点?若是,请求出定点,若否,请说明理由.
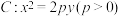 的焦点
的焦点 是椭圆
是椭圆 的一个焦点.
的一个焦点.(1)求
 的准线方程;
的准线方程;(2)若
 是直线
是直线 上的一动点,过
上的一动点,过 向
向 作两条切线,切点为M,N,试探究直线MN是否过定点?若是,请求出定点,若否,请说明理由.
作两条切线,切点为M,N,试探究直线MN是否过定点?若是,请求出定点,若否,请说明理由.
您最近一年使用:0次
解题方法
7 . 抛物线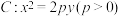 的焦点
的焦点 是椭圆
是椭圆 的一个焦点.
的一个焦点.
(1)求 的准线方程;
的准线方程;
(2)若 是直线
是直线 上的一动点,过
上的一动点,过 向
向 作两条切线,切点为M,N,当点
作两条切线,切点为M,N,当点 到直线
到直线 的距离最大值时,求点
的距离最大值时,求点 的坐标.
的坐标.
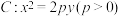 的焦点
的焦点 是椭圆
是椭圆 的一个焦点.
的一个焦点.(1)求
 的准线方程;
的准线方程;(2)若
 是直线
是直线 上的一动点,过
上的一动点,过 向
向 作两条切线,切点为M,N,当点
作两条切线,切点为M,N,当点 到直线
到直线 的距离最大值时,求点
的距离最大值时,求点 的坐标.
的坐标.
您最近一年使用:0次
解题方法
8 . 已知抛物线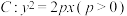 的焦点为F,过点
的焦点为F,过点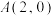 的直线l交C于M,N两点,当l与x轴垂直时,
的直线l交C于M,N两点,当l与x轴垂直时,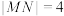 .
.
(1)求C的方程:
(2)在x轴上是否存在点P,使得 恒成立(O为坐标原点)?若存在求出坐标,若不存在说明理由.
恒成立(O为坐标原点)?若存在求出坐标,若不存在说明理由.
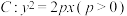 的焦点为F,过点
的焦点为F,过点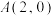 的直线l交C于M,N两点,当l与x轴垂直时,
的直线l交C于M,N两点,当l与x轴垂直时,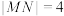 .
.(1)求C的方程:
(2)在x轴上是否存在点P,使得
 恒成立(O为坐标原点)?若存在求出坐标,若不存在说明理由.
恒成立(O为坐标原点)?若存在求出坐标,若不存在说明理由.
您最近一年使用:0次
2022-07-12更新
|
794次组卷
|
5卷引用:四川省泸州市龙马高中2022-2023学年高二上学期第二次月考数学(文)试题
四川省泸州市龙马高中2022-2023学年高二上学期第二次月考数学(文)试题四川省泸州市龙马高中2022-2023学年高二上学期第二次月考数学(理)试题内蒙古赤峰市2021-2022学年高二下学期期末考试数学(文)试题(已下线)第09讲 高考难点突破一:圆锥曲线的综合问题(定点问题) (精讲)-2(已下线)专题3-6 抛物线综合大题归类(讲+练)-【巅峰课堂】2023-2024学年高二数学热点题型归纳与培优练(人教A版2019选择性必修第一册)
9 . 已知F为抛物线 的焦点,点A,B在该抛物线上且位于x轴的两侧.
的焦点,点A,B在该抛物线上且位于x轴的两侧.
(1)若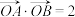 (其中O为坐标原点),求△ABO与△AFO面积之和的最小值;
(其中O为坐标原点),求△ABO与△AFO面积之和的最小值;
(2)若A,B,F三点共线,A,B处的切线交点为P,求P到F的最小距离.
 的焦点,点A,B在该抛物线上且位于x轴的两侧.
的焦点,点A,B在该抛物线上且位于x轴的两侧.(1)若
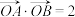 (其中O为坐标原点),求△ABO与△AFO面积之和的最小值;
(其中O为坐标原点),求△ABO与△AFO面积之和的最小值;(2)若A,B,F三点共线,A,B处的切线交点为P,求P到F的最小距离.
您最近一年使用:0次
10 . 已知直线l: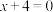 ,M为平面内一动点,过点M作直线l的垂线,垂足为N,且
,M为平面内一动点,过点M作直线l的垂线,垂足为N,且 (O为坐标原点).
(O为坐标原点).
(1)求动点M的轨迹E的方程;
(2)已知点P(0,2),直线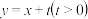 与曲线E交于A,B两点,直线PA,PB与曲线E的另一交点分别是点C,D,证明:直线CD的斜率为定值.
与曲线E交于A,B两点,直线PA,PB与曲线E的另一交点分别是点C,D,证明:直线CD的斜率为定值.
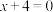 ,M为平面内一动点,过点M作直线l的垂线,垂足为N,且
,M为平面内一动点,过点M作直线l的垂线,垂足为N,且 (O为坐标原点).
(O为坐标原点).(1)求动点M的轨迹E的方程;
(2)已知点P(0,2),直线
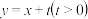 与曲线E交于A,B两点,直线PA,PB与曲线E的另一交点分别是点C,D,证明:直线CD的斜率为定值.
与曲线E交于A,B两点,直线PA,PB与曲线E的另一交点分别是点C,D,证明:直线CD的斜率为定值.
您最近一年使用:0次
2022-04-19更新
|
1251次组卷
|
6卷引用:四川省宜宾市叙州区第一中学校2022届高三下学期高考适应性考试数学(文)试题
四川省宜宾市叙州区第一中学校2022届高三下学期高考适应性考试数学(文)试题四川省宜宾市叙州区第一中学校2022届高三下学期高考适应性考试数学(理)试题黑龙江省哈尔滨市第九中学校2022届高三下学期第三次模拟考试数学(理)试题(已下线)回归教材重难点04 圆锥曲线-【查漏补缺】2022年高考数学(理)三轮冲刺过关黑龙江省哈尔滨市第九中学校2022届高三第三次模拟考试数学(文科)试题(已下线)第10讲 高考难点突破二:圆锥曲线的综合问题(定值问题) (精讲)



