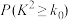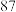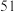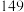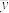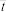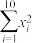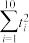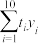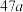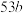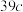名校
1 . 为提升学生综合素养,某中学为高二年级提供了“书法”和“剪纸”两门选修课.为了了解选择“书法”或“剪纸”是否与性别有关,调查了高二年级1500名学生的选择倾向,随机抽取了100名,统计选择两门课程人数如下表.
(1)补全 列联表;
列联表;
(2)根据小概率值 的独立性检验,在犯错概率不超过
的独立性检验,在犯错概率不超过 的前提下,是否可以认为选择“书法”或值“剪纸”与性别有关?(计算结果保留到小数点后三位)参考公式:
的前提下,是否可以认为选择“书法”或值“剪纸”与性别有关?(计算结果保留到小数点后三位)参考公式: ,其中
,其中 .
.
选书法 | 选剪纸 | 合计 | |
男生 | 40 | 50 | |
女生 | |||
合计 | 30 |
 列联表;
列联表;(2)根据小概率值
 的独立性检验,在犯错概率不超过
的独立性检验,在犯错概率不超过 的前提下,是否可以认为选择“书法”或值“剪纸”与性别有关?(计算结果保留到小数点后三位)参考公式:
的前提下,是否可以认为选择“书法”或值“剪纸”与性别有关?(计算结果保留到小数点后三位)参考公式: ,其中
,其中 .
. | 0.100 | 0.050 | 0.025 |
 | 2.706 | 3.841 | 5.024 |
您最近一年使用:0次
解题方法
2 . 2018年8月16日,中共中央政治局常务委员会召开会议,听取关于吉林长春长生公司问题疫苗案件调查及有关问责情况的汇报,中共中央总书记习近平主持会议并发表重要讲话.会议强调,疫苗关系人民群众健康,关系公共卫生安全和国家安全.因此,疫苗行业在生产、运输、储存、使用等任何一个环节都容不得半点瑕疵.国家规定,疫苗在上市前必须经过严格的检测,并通过临床实验获得相关数据,以保证疫苗使用的安全和有效.某生物制品研究所将某一型号疫苗用在动物小白鼠身上进行科研和临床实验,得到统计数据如下:
现从未注射疫苗的小白鼠中任取1只,取到“感染病毒”的小白鼠的概率为 .
.
(1)求 列联表中的数据
列联表中的数据 ,
, ,
, ,
, 的值;
的值;
(2)能否有 把握认为注射此种疫苗有效?请说明理由;
把握认为注射此种疫苗有效?请说明理由;
(3)在感染病毒的小白鼠中,按未注射疫苗和注射疫苗的比例抽取5只进行病例分析,然后从这五只小白鼠中随机抽取3只对注射疫苗情况进行核实,记 为3只中未注射疫苗的小白鼠的只数,求
为3只中未注射疫苗的小白鼠的只数,求 的分布列和期望.
的分布列和期望.
附: ,
, .
.
未感染病毒 | 感染病毒 | 总计 | |
未注射疫苗 | 40 |
|
|
注射疫苗 | 60 |
|
|
总计 | 100 | 100 | 200 |
 .
.(1)求
 列联表中的数据
列联表中的数据 ,
, ,
, ,
, 的值;
的值;(2)能否有
 把握认为注射此种疫苗有效?请说明理由;
把握认为注射此种疫苗有效?请说明理由;(3)在感染病毒的小白鼠中,按未注射疫苗和注射疫苗的比例抽取5只进行病例分析,然后从这五只小白鼠中随机抽取3只对注射疫苗情况进行核实,记
 为3只中未注射疫苗的小白鼠的只数,求
为3只中未注射疫苗的小白鼠的只数,求 的分布列和期望.
的分布列和期望.附:
 ,
, .
.
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
您最近一年使用:0次
名校
3 . 已知一组样本数据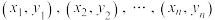 ,根据这组数据的散点图分析x与y之间的线性相关关系,若求得其线性回归方程为
,根据这组数据的散点图分析x与y之间的线性相关关系,若求得其线性回归方程为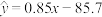 ,则在样本点
,则在样本点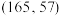 处的残差为( )
处的残差为( )
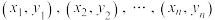 ,根据这组数据的散点图分析x与y之间的线性相关关系,若求得其线性回归方程为
,根据这组数据的散点图分析x与y之间的线性相关关系,若求得其线性回归方程为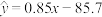 ,则在样本点
,则在样本点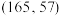 处的残差为( )
处的残差为( )A.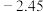 | B.2.45 | C.3.45 | D.54.55 |
您最近一年使用:0次
2022-07-08更新
|
1015次组卷
|
5卷引用:北京市朝阳区2021-2022学年高二下学期期末质量检测数学试题
北京市朝阳区2021-2022学年高二下学期期末质量检测数学试题(已下线)专题06 离散型随机变量分布列及成对数据统计分析6种常考题型归类-2河北省石家庄市2023-2024学年高二下学期7月期末考试数学试题河北省石家庄十五中2023-2024学年高二下学期期末数学试题(已下线)专题10-1 概率统计(选填)-1
解题方法
4 . 为了了解居家学习期间性别因素是否对学生体育锻炼的经常性有影响,某校随机抽取了40名学生进行调查,按照性别和体育锻炼情况整理出如下的 列联表:
列联表:
注: 独立性检验中,
独立性检验中,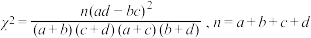 .
.
常用的小概率值和相应的临界值如下表:
根据这些数据,给出下列四个结论:
①依据频率稳定于概率的原理,可以认为性别对体育锻炼的经常性有影响;
②依据频率稳定于概率的原理,可以认为性别对体育锻炼的经常性没有影响;
③根据小概率值 的独立性检验,可以认为性别对体育锻炼的经常性有影响,这个推断犯错误的概率不超过0.05;
的独立性检验,可以认为性别对体育锻炼的经常性有影响,这个推断犯错误的概率不超过0.05;
④根据小概率值 的独立性检验,没有充分证据推断性别对体育锻炼的经常性有影响,因此可以认为性别对体育锻炼的经常性没有影响.
的独立性检验,没有充分证据推断性别对体育锻炼的经常性有影响,因此可以认为性别对体育锻炼的经常性没有影响.
其中,正确结论的序号是( )
 列联表:
列联表:| 性别 | 锻炼情况 | 合计 | |
| 不经常 | 经常 | ||
| 女生/人 | 14 | 7 | 21 |
| 男生/人 | 8 | 11 | 19 |
| 合计/人 | 22 | 18 | 40 |
 独立性检验中,
独立性检验中,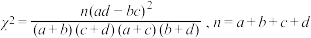 .
.常用的小概率值和相应的临界值如下表:
 | 0.1 | 0.05 | 0.01 | 0.005 | 0.001 |
 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
①依据频率稳定于概率的原理,可以认为性别对体育锻炼的经常性有影响;
②依据频率稳定于概率的原理,可以认为性别对体育锻炼的经常性没有影响;
③根据小概率值
 的独立性检验,可以认为性别对体育锻炼的经常性有影响,这个推断犯错误的概率不超过0.05;
的独立性检验,可以认为性别对体育锻炼的经常性有影响,这个推断犯错误的概率不超过0.05;④根据小概率值
 的独立性检验,没有充分证据推断性别对体育锻炼的经常性有影响,因此可以认为性别对体育锻炼的经常性没有影响.
的独立性检验,没有充分证据推断性别对体育锻炼的经常性有影响,因此可以认为性别对体育锻炼的经常性没有影响.其中,正确结论的序号是( )
| A.①③ | B.①④ | C.②③ | D.②④ |
您最近一年使用:0次
2022-07-08更新
|
966次组卷
|
10卷引用:北京市朝阳区2021-2022学年高二下学期期末质量检测数学试题
北京市朝阳区2021-2022学年高二下学期期末质量检测数学试题(已下线)专题06 离散型随机变量分布列及成对数据统计分析6种常考题型归类-2(已下线)第八章 成对数据的统计分析(B卷·能力提升练)-【单元测试】2022-2023学年高二数学分层训练AB卷(人教A版2019)(已下线)9.2独立性检验(2)(已下线)第9章 统计 单元综合检测(已下线)8.3.2 独立性检验(分层作业)(已下线)8.3 列联表与独立性检验(题型专训)(已下线)专题10-1 概率统计(选填)-2(已下线)第三节 成对数据的统计分析(第二课时) B卷素养养成卷(已下线)第四章 统计 专题三 独立性检验 微点3 独立性检验(三)【培优版】
5 . 在新型冠状病毒疫情期间,某高中学校实施线上教学,为了解线上教学的效果,随机抽取了100名学生对线上教学效果进行评分(满分100分),记低于80的评分为“效果一般”,不低于80分为“效果较好”
(1)根据所给数据完成下列表格;
(2)用(1)中表格的数据估计全校线上教学的效果,用频率估计概率.从该校学生中任意抽取3人,记所抽取的3人中认为线上教学“效果一般”的人数为X,求X的分布列和数学期望及方差.
(1)根据所给数据完成下列表格;
| 效果一般 | 效果较好 | 合计 | |
| 男 | 25 | 45 | |
| 女 | 40 | ||
| 合计 |
您最近一年使用:0次
2022-05-16更新
|
444次组卷
|
3卷引用:北京市第八十中学2021-2022学年高二下学期期中考试数学试题
名校
6 . 下表是某饮料专卖店一天卖出奶茶的杯数y与当天气温x(单位: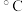 )的对比表,已知表中数据计算得到y关于x的线性回归方程为
)的对比表,已知表中数据计算得到y关于x的线性回归方程为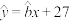 ,则相应于点
,则相应于点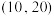 的残差为
的残差为________ .
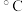 )的对比表,已知表中数据计算得到y关于x的线性回归方程为
)的对比表,已知表中数据计算得到y关于x的线性回归方程为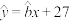 ,则相应于点
,则相应于点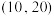 的残差为
的残差为气温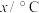 | 5 | 10 | 15 | 20 | 25 |
| 杯数y | 26 | 20 | 16 | 14 | 14 |
您最近一年使用:0次
2021-08-17更新
|
670次组卷
|
5卷引用:北京市朝阳区中央美术学院附属实验学校2021-2022学年高二下学期期中数学试题
北京市朝阳区中央美术学院附属实验学校2021-2022学年高二下学期期中数学试题广西浦北中学2020-2021学年高二3月月考数学(文)试题浙江省宁波市北仑中学2022-2023学年高二上学期期中数学试题(1班使用)(已下线)专题04 第八章 成对数据的统计分析--高二期末考点大串讲(人教A版2019)(已下线)第四章 统计 专题二 统计相关性与回归分析 微点3 相关分析与回归分析(三)【培优版】
7 . 某调查机构在一个小区随机采访了 位业主,统计他们的每周跑步时间,将每周跑步时间不小于
位业主,统计他们的每周跑步时间,将每周跑步时间不小于 分钟的人称为“跑步爱好者”,每周跑步时间小于
分钟的人称为“跑步爱好者”,每周跑步时间小于 分钟的人称为“非跑步爱好者”,得到
分钟的人称为“非跑步爱好者”,得到 列联表如下所示.
列联表如下所示.
(1)能否有99%的把握认为是否为“跑步爱好者”与性别有关?
(2)若一次跑步时间(单位:分钟)在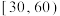 内积
内积 分,在
分,在 内积
内积 分,设甲、乙两名“跑步爱好者”的跑步时间相互独立,且甲、乙两人的一次跑步时间在
分,设甲、乙两名“跑步爱好者”的跑步时间相互独立,且甲、乙两人的一次跑步时间在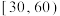 内的概率分别为
内的概率分别为 ,
, ,在
,在 内的概率分别为
内的概率分别为 ,
, ,甲、乙两人一次跑步积分之和为随机变量
,甲、乙两人一次跑步积分之和为随机变量 ,求
,求 的分布列与数学期望.
的分布列与数学期望.
参考公式及数据: ,其中
,其中 .
.
 位业主,统计他们的每周跑步时间,将每周跑步时间不小于
位业主,统计他们的每周跑步时间,将每周跑步时间不小于 分钟的人称为“跑步爱好者”,每周跑步时间小于
分钟的人称为“跑步爱好者”,每周跑步时间小于 分钟的人称为“非跑步爱好者”,得到
分钟的人称为“非跑步爱好者”,得到 列联表如下所示.
列联表如下所示.跑步爱好者 | 非跑步爱好者 | 合计 | |
男性 |
|
|
|
女性 |
|
|
|
合计 |
|
|
|
(2)若一次跑步时间(单位:分钟)在
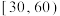 内积
内积 分,在
分,在 内积
内积 分,设甲、乙两名“跑步爱好者”的跑步时间相互独立,且甲、乙两人的一次跑步时间在
分,设甲、乙两名“跑步爱好者”的跑步时间相互独立,且甲、乙两人的一次跑步时间在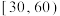 内的概率分别为
内的概率分别为 ,
, ,在
,在 内的概率分别为
内的概率分别为 ,
, ,甲、乙两人一次跑步积分之和为随机变量
,甲、乙两人一次跑步积分之和为随机变量 ,求
,求 的分布列与数学期望.
的分布列与数学期望.参考公式及数据:
 ,其中
,其中 .
.
|
|
|
|
|
|
|
|
|
|
您最近一年使用:0次
2021-08-06更新
|
322次组卷
|
3卷引用:北京市昌平区新学道临川学校2021-2022学年高二(北京班)下学期期中考试数学试题
名校
解题方法
8 . 某公司对某产品作市场调查,获得了该产品的定价 (单位:万元/吨)和一天的销量
(单位:万元/吨)和一天的销量 吨)的一组数据,根据这组数据制作了如下统计表和散点图.
吨)的一组数据,根据这组数据制作了如下统计表和散点图.
表中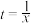 .
.
(Ⅰ)根据散点图判断, 与
与 哪一个更适合作为
哪一个更适合作为 关于
关于 的经验回归方程;(给出判断即可,不必说明理由)
的经验回归方程;(给出判断即可,不必说明理由)
(Ⅱ)根据(Ⅰ)的判断结果,建立 关于
关于 的经验回归方程;
的经验回归方程;
(Ⅲ)若生产1吨该产品的成本为0.25万元,依据(Ⅱ)的经验回归方程,预计每吨定价多少时,该产品一天的销售利润最大?最大利润是多少?
(经验回归方程 中,
中,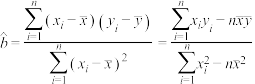 ,
,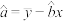 )
)
 (单位:万元/吨)和一天的销量
(单位:万元/吨)和一天的销量 吨)的一组数据,根据这组数据制作了如下统计表和散点图.
吨)的一组数据,根据这组数据制作了如下统计表和散点图.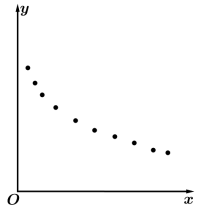
|
|
|
|
|
|
|
0.33 | 10 | 3 | 0.164 | 100 | 68 | 350 |
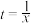 .
.(Ⅰ)根据散点图判断,
 与
与 哪一个更适合作为
哪一个更适合作为 关于
关于 的经验回归方程;(给出判断即可,不必说明理由)
的经验回归方程;(给出判断即可,不必说明理由)(Ⅱ)根据(Ⅰ)的判断结果,建立
 关于
关于 的经验回归方程;
的经验回归方程;(Ⅲ)若生产1吨该产品的成本为0.25万元,依据(Ⅱ)的经验回归方程,预计每吨定价多少时,该产品一天的销售利润最大?最大利润是多少?
(经验回归方程
 中,
中,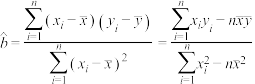 ,
,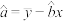 )
)
您最近一年使用:0次
2021-07-26更新
|
1054次组卷
|
6卷引用:北京市通州区2020-2021学年高二下学期期末数学试题
解题方法
9 . 根据国家电影局发布的数据,2020年中国电影总票房为204.17亿,年度票房首度超越北美,成为2020年全球第一大电影市场.国产历史战争题材影片《八佰》和《金刚川》合力贡献了国内全年票房的 .我们用简单随机抽样的方法,分别从这两部电影的购票观众中各随调查了100名观众,得到结果如下:图1是购票观众年龄分布情况;图2是购票观众性别分布情况.
.我们用简单随机抽样的方法,分别从这两部电影的购票观众中各随调查了100名观众,得到结果如下:图1是购票观众年龄分布情况;图2是购票观众性别分布情况.
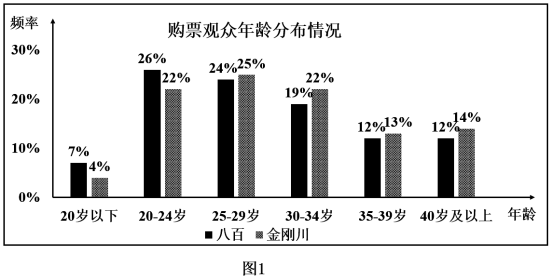

(1)记 表示事件:“观看电影《八佰》的观众年龄低于30岁”,根据图1的数据,估计
表示事件:“观看电影《八佰》的观众年龄低于30岁”,根据图1的数据,估计 的概率;
的概率;
(2)现从参与调查的电影《金刚川》的100名购票观众中随机抽取两名依次进行电话回访,求在第1次抽到男性观众的条件下,第2次仍抽到男性观众的概率.
(3)填写下面的 列联表,并根据小概率值
列联表,并根据小概率值 的独立性检验,分析男性观众与女性观众对这两部历史战争题材影片的选择是否有差异?
的独立性检验,分析男性观众与女性观众对这两部历史战争题材影片的选择是否有差异?
附:
 .我们用简单随机抽样的方法,分别从这两部电影的购票观众中各随调查了100名观众,得到结果如下:图1是购票观众年龄分布情况;图2是购票观众性别分布情况.
.我们用简单随机抽样的方法,分别从这两部电影的购票观众中各随调查了100名观众,得到结果如下:图1是购票观众年龄分布情况;图2是购票观众性别分布情况.

(1)记
 表示事件:“观看电影《八佰》的观众年龄低于30岁”,根据图1的数据,估计
表示事件:“观看电影《八佰》的观众年龄低于30岁”,根据图1的数据,估计 的概率;
的概率;(2)现从参与调查的电影《金刚川》的100名购票观众中随机抽取两名依次进行电话回访,求在第1次抽到男性观众的条件下,第2次仍抽到男性观众的概率.
(3)填写下面的
 列联表,并根据小概率值
列联表,并根据小概率值 的独立性检验,分析男性观众与女性观众对这两部历史战争题材影片的选择是否有差异?
的独立性检验,分析男性观众与女性观众对这两部历史战争题材影片的选择是否有差异?影片 | 女性观众 | 男性观众 | 总计 | ||||
《八佰》 |
|
| 100 | ||||
《金刚川》 |
|
| 100 | ||||
总计 | 86 | 114 | 200 | ||||
| 0.1 | 0.05 | 0.01 | 0.001 | |||
| 2.706 | 3.841 | 6.635 | 10.828 | |||

您最近一年使用:0次
名校
10 . 在这次新冠肺炎疫情中,各地的医务工作者和各行各业都纷纷支援湖北,包括很多国际友人.广大民众也广泛响应号召,自行在家隔离.
(1)现在假设有一对夫妻响应号召,自行在家隔离.现在假设这两人是新冠无症状携带者的概率均为0.5,且每人是否发病是相互独立事件.
①如果两人在家共用一些物品,又没有良好的卫生习惯(即病毒互相传染的可能性为100%),求:最后患病人数的分布列和期望(假设携带就一定会发病).
②如果两人在家都有良好的卫生习惯,互相之间病毒没有传染可能.求:最后患病人数的分布列和期望(假设携带就一定会发病).
③列举至少两条居家避免互相传染的方法.
④假设这是一个大家庭,有n个人一起居家隔离,在②的条件下,则最终患病人数的期望为 ,方差为 .
(2)我们知道一个药物是否对病毒有效,要做重重试验,首先是体外细胞试验,然后是体内细胞试验,然后才能真正进入人体试验阶段.下面介绍一个医学史上的双盲试验:“1947年,希尔将107名肺结核病人分为随机分为两组:其中试验组55人,用链霉素进行治疗,对照组52人,卧床休息一因为别无他法. 经过6个月的治疗,试验组的55人有93%依然存活,而对照组只有73%依然存活.”根据这段试验描述,自己列一个二联表,并检验使用链霉素是否对提高肺结核的存活率有影响.
(3)下图是截止至2020年2月17日止,中国疾控中心针对这次新冠病毒七万多确诊人数所做的年龄分布柱状图.请结合该图写出至少两个不同类型的统计结论(例如数字特征、分布类型等).并写出你结论的判断依据.
[提示]可选择的数字特征之一及方向:初步判断哪个图中的年龄均值最大.最后;愿这次疫情早日结束,中国加油!

(1)现在假设有一对夫妻响应号召,自行在家隔离.现在假设这两人是新冠无症状携带者的概率均为0.5,且每人是否发病是相互独立事件.
①如果两人在家共用一些物品,又没有良好的卫生习惯(即病毒互相传染的可能性为100%),求:最后患病人数的分布列和期望(假设携带就一定会发病).
②如果两人在家都有良好的卫生习惯,互相之间病毒没有传染可能.求:最后患病人数的分布列和期望(假设携带就一定会发病).
③列举至少两条居家避免互相传染的方法.
④假设这是一个大家庭,有n个人一起居家隔离,在②的条件下,则最终患病人数的期望为 ,方差为 .
(2)我们知道一个药物是否对病毒有效,要做重重试验,首先是体外细胞试验,然后是体内细胞试验,然后才能真正进入人体试验阶段.下面介绍一个医学史上的双盲试验:“1947年,希尔将107名肺结核病人分为随机分为两组:其中试验组55人,用链霉素进行治疗,对照组52人,卧床休息一因为别无他法. 经过6个月的治疗,试验组的55人有93%依然存活,而对照组只有73%依然存活.”根据这段试验描述,自己列一个二联表,并检验使用链霉素是否对提高肺结核的存活率有影响.
(3)下图是截止至2020年2月17日止,中国疾控中心针对这次新冠病毒七万多确诊人数所做的年龄分布柱状图.请结合该图写出至少两个不同类型的统计结论(例如数字特征、分布类型等).并写出你结论的判断依据.
[提示]可选择的数字特征之一及方向:初步判断哪个图中的年龄均值最大.最后;愿这次疫情早日结束,中国加油!

您最近一年使用:0次