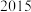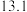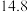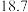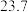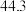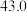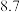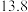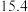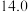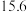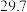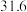1 . 某人投掷两枚骰子,取其中一枚的点数记为点 的横坐标
的横坐标 ,另一枚的点数记为点
,另一枚的点数记为点 的纵坐标
的纵坐标 ,令事件
,令事件 “
“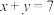 ”,事件
”,事件 “
“ 为奇数”.
为奇数”.
(1)证明:事件 相互独立;
相互独立;
(2)若连续抛掷这两枚骰子三次,求点 在圆
在圆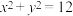 内的次数
内的次数 的分布列与期望.
的分布列与期望.
 的横坐标
的横坐标 ,另一枚的点数记为点
,另一枚的点数记为点 的纵坐标
的纵坐标 ,令事件
,令事件 “
“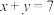 ”,事件
”,事件 “
“ 为奇数”.
为奇数”.(1)证明:事件
 相互独立;
相互独立;(2)若连续抛掷这两枚骰子三次,求点
 在圆
在圆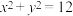 内的次数
内的次数 的分布列与期望.
的分布列与期望.
您最近一年使用:0次
解题方法
2 . 甲、乙两个篮球队在4次不同比赛中的得分情况如下:
(1)在4次比赛中,求甲队的平均得分;
(2)分别从甲、乙两队的4次比赛得分中各随机选取1次,求这2个比赛得分之差的绝对值为1的概率;
(3)甲,乙两队得分数据的方差分别记为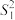 ,
,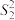 ,试判断
,试判断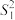 与
与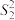 的大小(结论不要求证明)
的大小(结论不要求证明)
甲队 | 88 | 91 | 93 | 96 |
乙队 | 89 | 94 | 97 | 92 |
(2)分别从甲、乙两队的4次比赛得分中各随机选取1次,求这2个比赛得分之差的绝对值为1的概率;
(3)甲,乙两队得分数据的方差分别记为
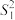 ,
,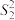 ,试判断
,试判断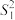 与
与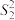 的大小(结论不要求证明)
的大小(结论不要求证明)
您最近一年使用:0次
2024-01-29更新
|
204次组卷
|
2卷引用:北京市石景山区2023-2024学年高一上学期期末考试数学试卷
名校
解题方法
3 . 不粘锅是家庭常用的厨房用具,近期,某市消费者权益保护委员会从市场上购买了12款不粘锅商品,并委托第三方检测机构进行检测,本次选取了食物接触材料安全项目中与消费者使用密切相关的6项性能项目进行比较试验,性能检测项目包含不粘性、耐磨性、耐碱性、手柄温度、温度均匀性和使用体验等6个指标.其中消费者关注最多的两个指标“不沾性、耐磨性”检测结果的数据如下:
(Ⅰ级代表性能优秀,Ⅱ级代表性能较好)
(1)从这12个品牌的样本数据中随机选取两个品牌的数据,求这两个品牌的“不粘性”性能都是Ⅰ级的概率:
(2)从前六个品牌、后六个品牌中各随机选取两个品牌的数据,求两个指标“不沾性、耐磨性”都是Ⅰ级的品牌个数恰为2个的概率;
(3)顾客甲从品牌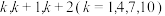 中随机选取1个品牌,用“
中随机选取1个品牌,用“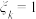 ”表示选取的品牌两个指标“不沾性、耐磨性”都是Ⅰ级,“
”表示选取的品牌两个指标“不沾性、耐磨性”都是Ⅰ级,“ ”表示选取的品牌两个指标“不沾性、耐磨性”不都是Ⅰ级(k=1,4,7,10).写出方差
”表示选取的品牌两个指标“不沾性、耐磨性”不都是Ⅰ级(k=1,4,7,10).写出方差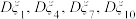 的大小关系(结论不要求证明).
的大小关系(结论不要求证明).
检测结果 | 检测结果 | |||||||
序号 | 品牌名称 | 不粘性 | 耐磨性 | 序号 | 品牌名称 | 不粘性 | 耐磨性 | |
1 | 品牌1 | Ⅰ级 | Ⅰ级 | 7 | 品牌7 | Ⅰ级 | Ⅰ级 | |
2 | 品牌2 | Ⅱ级 | Ⅰ级 | 8 | 品牌8 | Ⅰ级 | Ⅰ级 | |
3 | 品牌3 | Ⅰ级 | Ⅰ级 | 9 | 品牌9 | Ⅱ级 | Ⅱ级 | |
4 | 品牌4 | Ⅱ级 | Ⅱ级 | 10 | 品牌10 | Ⅱ级 | Ⅱ级 | |
5 | 品牌5 | Ⅰ级 | Ⅰ级 | 11 | 品牌11 | Ⅱ级 | Ⅱ级 | |
6 | 品牌6 | Ⅱ级 | Ⅰ级 | 12 | 品牌12 | Ⅱ级 | Ⅱ级 | |
(1)从这12个品牌的样本数据中随机选取两个品牌的数据,求这两个品牌的“不粘性”性能都是Ⅰ级的概率:
(2)从前六个品牌、后六个品牌中各随机选取两个品牌的数据,求两个指标“不沾性、耐磨性”都是Ⅰ级的品牌个数恰为2个的概率;
(3)顾客甲从品牌
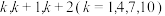 中随机选取1个品牌,用“
中随机选取1个品牌,用“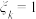 ”表示选取的品牌两个指标“不沾性、耐磨性”都是Ⅰ级,“
”表示选取的品牌两个指标“不沾性、耐磨性”都是Ⅰ级,“ ”表示选取的品牌两个指标“不沾性、耐磨性”不都是Ⅰ级(k=1,4,7,10).写出方差
”表示选取的品牌两个指标“不沾性、耐磨性”不都是Ⅰ级(k=1,4,7,10).写出方差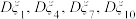 的大小关系(结论不要求证明).
的大小关系(结论不要求证明).
您最近一年使用:0次
解题方法
4 . 为研究中国工业机器人产量和销量的变化规律,收集得到了 年工业机器人的产量和销量数据,如下表所示.
年工业机器人的产量和销量数据,如下表所示.
记 年工业机器人产量的中位数为
年工业机器人产量的中位数为 ,销量的中位数为
,销量的中位数为 .定义产销率为“
.定义产销率为“ ”.
”.
(1)从 年中随机取
年中随机取 年,求工业机器人的产销率大于
年,求工业机器人的产销率大于 的概率;
的概率;
(2)从 年这
年这 年中随机取
年中随机取 年,这
年,这 年中有
年中有 年工业机器人的产量不小于
年工业机器人的产量不小于 ,有
,有 年工业机器人的销量不小于
年工业机器人的销量不小于 .记
.记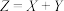 ,求
,求 的分布列和数学期望
的分布列和数学期望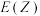 ;
;
(3)从哪年开始的连续 年中随机取
年中随机取 年,工业机器人的产销率超过
年,工业机器人的产销率超过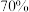 的概率最小.结论不要求证明
的概率最小.结论不要求证明
 年工业机器人的产量和销量数据,如下表所示.
年工业机器人的产量和销量数据,如下表所示.年份 |
|
|
|
|
|
|
|
|
|
产量万台 |
|
|
|
|
|
|
|
|
|
销量万台 |
|
|
|
|
|
|
|
|
|
 年工业机器人产量的中位数为
年工业机器人产量的中位数为 ,销量的中位数为
,销量的中位数为 .定义产销率为“
.定义产销率为“ ”.
”.(1)从
 年中随机取
年中随机取 年,求工业机器人的产销率大于
年,求工业机器人的产销率大于 的概率;
的概率;(2)从
 年这
年这 年中随机取
年中随机取 年,这
年,这 年中有
年中有 年工业机器人的产量不小于
年工业机器人的产量不小于 ,有
,有 年工业机器人的销量不小于
年工业机器人的销量不小于 .记
.记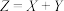 ,求
,求 的分布列和数学期望
的分布列和数学期望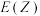 ;
;(3)从哪年开始的连续
 年中随机取
年中随机取 年,工业机器人的产销率超过
年,工业机器人的产销率超过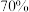 的概率最小.结论不要求证明
的概率最小.结论不要求证明
您最近一年使用:0次
名校
5 . 我国周朝时期的商高提出了“勾三股四弦五”的勾股定理的特例.在西方,最早提出并证明此定理的为公元前6世纪古希腊的毕达哥拉斯学派,他们用演绎法证明了直角三角形斜边的平方等于两直角边的平方之和.在3,4,5,6,8,10,12,13这8个数中任取3个数,这3个数恰好可以组成勾股定理关系的概率为( )
A. | B. | C.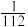 | D.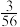 |
您最近一年使用:0次
2024-01-22更新
|
483次组卷
|
4卷引用:河北省张家口市2024届高三上学期期末数学试题
河北省张家口市2024届高三上学期期末数学试题(已下线)专题16 组合7种常见考法归类-【寒假自学课】2024年高二数学寒假提升学与练(苏教版2019)云南省开远市第一中学校2023-2024学年高二下学期开学考试数学试题(已下线)江苏省淮阴中学等四校2024届高三下学期期初测试联考数学试卷
名校
解题方法
6 . 一个袋子中装有大小和质地相同的4个球,其中有2个红球(标号为1和2),2个白球(标号为3和4),甲、乙两人先后从袋中不放回地各摸出1个球.设“甲摸到红球”为事件 ,“乙摸到红球”为事件
,“乙摸到红球”为事件 .
.
(1)小明同学认为:由于甲先摸球,所以事件 发生的可能性大于
发生的可能性大于 发生的可能性.小明的判断是否正确,请说明理由;
发生的可能性.小明的判断是否正确,请说明理由;
(2)判断事件 与
与 是否相互独立,并证明.
是否相互独立,并证明.
 ,“乙摸到红球”为事件
,“乙摸到红球”为事件 .
.(1)小明同学认为:由于甲先摸球,所以事件
 发生的可能性大于
发生的可能性大于 发生的可能性.小明的判断是否正确,请说明理由;
发生的可能性.小明的判断是否正确,请说明理由;(2)判断事件
 与
与 是否相互独立,并证明.
是否相互独立,并证明.
您最近一年使用:0次
2023-06-29更新
|
495次组卷
|
5卷引用:专题07 概率-《期末真题分类汇编》(新高考专用)
名校
7 . 在如图所示的直角梯形 中,利用“两个全等的直角三角形和一个等腰直角三角形的面积之和等于直角梯形的面积”.可以简洁明了地推证出勾股定理,把这一证明方法称为“总统证法”.设
中,利用“两个全等的直角三角形和一个等腰直角三角形的面积之和等于直角梯形的面积”.可以简洁明了地推证出勾股定理,把这一证明方法称为“总统证法”.设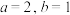 ,在梯形
,在梯形 中随机取一点,则此点取自等腰直角三角形
中随机取一点,则此点取自等腰直角三角形 中(阴影部分)的概率是( )
中(阴影部分)的概率是( )
 中,利用“两个全等的直角三角形和一个等腰直角三角形的面积之和等于直角梯形的面积”.可以简洁明了地推证出勾股定理,把这一证明方法称为“总统证法”.设
中,利用“两个全等的直角三角形和一个等腰直角三角形的面积之和等于直角梯形的面积”.可以简洁明了地推证出勾股定理,把这一证明方法称为“总统证法”.设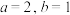 ,在梯形
,在梯形 中随机取一点,则此点取自等腰直角三角形
中随机取一点,则此点取自等腰直角三角形 中(阴影部分)的概率是( )
中(阴影部分)的概率是( )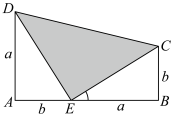
A. | B.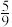 | C. | D.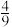 |
您最近一年使用:0次
2023-05-13更新
|
210次组卷
|
3卷引用:陕西省榆林市第一中学2024届高三第一次模拟考试理科数学试题
解题方法
8 . 三国时期数学家赵爽为了证明勾股定理,创制了一幅如图所示的“弦图”,后人称之为“赵爽弦图”,它由四个全等的直角三角形和一个正方形构成.现对该图进行涂色,有5种不同的颜色提供选择,相邻区域所涂颜色不同.在所有的涂色方案中随机选择一种方案,该方案恰好只用到三种颜色的概率是( )
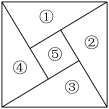
A.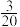 | B.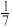 | C. | D. |
您最近一年使用:0次
名校
解题方法
9 . 第 届冬季奥林匹克运动会于
届冬季奥林匹克运动会于 年
年 月
月 日在北京、张家口盛大开幕.为保障本届冬奥会顺利运行,共招募约
日在北京、张家口盛大开幕.为保障本届冬奥会顺利运行,共招募约 万人参与赛会志愿服务.赛会共设对外联络服务、竞赛运行服务、媒体运行与转播服务、场馆运行服务、市场开发服务、人力资源服务、技术运行服务、文化展示服务、赛会综合服务、安保服务、交通服务、其他共
万人参与赛会志愿服务.赛会共设对外联络服务、竞赛运行服务、媒体运行与转播服务、场馆运行服务、市场开发服务、人力资源服务、技术运行服务、文化展示服务、赛会综合服务、安保服务、交通服务、其他共 类志愿服务.
类志愿服务.
(1)甲、乙两名志愿者被随机分配到不同类志愿服务中,每人只参加一类志愿服务.已知甲被分配到对外联络服务,求乙被分配到场馆运行服务的概率是多少?
(2)已知来自某中学的每名志愿者被分配到文化展示服务类的概率是 ,设来自该中学的
,设来自该中学的 名志愿者被分配到文化展示服务类的人数为
名志愿者被分配到文化展示服务类的人数为 ,求
,求 的分布列与期望;
的分布列与期望;
(3) 万名志愿者中,
万名志愿者中, 岁人群占比达到
岁人群占比达到 ,为了解志愿者对某一活动方案是否支持,通过分层抽样获得如下数据:
,为了解志愿者对某一活动方案是否支持,通过分层抽样获得如下数据:
假设所有志愿者对活动方案是否支持相互独立.将志愿者支持方案的概率估计值记为 ,去掉其它人群志愿者,支持方案的概率估计值记为
,去掉其它人群志愿者,支持方案的概率估计值记为 ,试比较
,试比较 与
与 的大小.(结论不要求证明)
的大小.(结论不要求证明)
 届冬季奥林匹克运动会于
届冬季奥林匹克运动会于 年
年 月
月 日在北京、张家口盛大开幕.为保障本届冬奥会顺利运行,共招募约
日在北京、张家口盛大开幕.为保障本届冬奥会顺利运行,共招募约 万人参与赛会志愿服务.赛会共设对外联络服务、竞赛运行服务、媒体运行与转播服务、场馆运行服务、市场开发服务、人力资源服务、技术运行服务、文化展示服务、赛会综合服务、安保服务、交通服务、其他共
万人参与赛会志愿服务.赛会共设对外联络服务、竞赛运行服务、媒体运行与转播服务、场馆运行服务、市场开发服务、人力资源服务、技术运行服务、文化展示服务、赛会综合服务、安保服务、交通服务、其他共 类志愿服务.
类志愿服务.(1)甲、乙两名志愿者被随机分配到不同类志愿服务中,每人只参加一类志愿服务.已知甲被分配到对外联络服务,求乙被分配到场馆运行服务的概率是多少?
(2)已知来自某中学的每名志愿者被分配到文化展示服务类的概率是
 ,设来自该中学的
,设来自该中学的 名志愿者被分配到文化展示服务类的人数为
名志愿者被分配到文化展示服务类的人数为 ,求
,求 的分布列与期望;
的分布列与期望;(3)
 万名志愿者中,
万名志愿者中, 岁人群占比达到
岁人群占比达到 ,为了解志愿者对某一活动方案是否支持,通过分层抽样获得如下数据:
,为了解志愿者对某一活动方案是否支持,通过分层抽样获得如下数据: 岁人群 岁人群 | 其它人群 | |||
| 支持 | 不支持 | 支持 | 不支持 | |
| 方案 |  人 人 |  人 人 |  人 人 |  人 人 |
 ,去掉其它人群志愿者,支持方案的概率估计值记为
,去掉其它人群志愿者,支持方案的概率估计值记为 ,试比较
,试比较 与
与 的大小.(结论不要求证明)
的大小.(结论不要求证明)
您最近一年使用:0次
2022-04-01更新
|
916次组卷
|
6卷引用:北京市和平街第一中学2023-2024学年高二下学期期中调研数学试卷
真题
名校
10 . 在校运动会上,只有甲、乙、丙三名同学参加铅球比赛,比赛成绩达到 以上(含
以上(含 )的同学将获得优秀奖.为预测获得优秀奖的人数及冠军得主,收集了甲、乙、丙以往的比赛成绩,并整理得到如下数据(单位:m):
)的同学将获得优秀奖.为预测获得优秀奖的人数及冠军得主,收集了甲、乙、丙以往的比赛成绩,并整理得到如下数据(单位:m):
甲:9.80,9.70,9.55,9.54,9.48,9.42,9.40,9.35,9.30,9.25;
乙:9.78,9.56,9.51,9.36,9.32,9.23;
丙:9.85,9.65,9.20,9.16.
假设用频率估计概率,且甲、乙、丙的比赛成绩相互独立.
(1)估计甲在校运动会铅球比赛中获得优秀奖的概率;
(2)设X是甲、乙、丙在校运动会铅球比赛中获得优秀奖的总人数,估计X的数学期望E(X);
(3)在校运动会铅球比赛中,甲、乙、丙谁获得冠军的概率估计值最大?(结论不要求证明)
 以上(含
以上(含 )的同学将获得优秀奖.为预测获得优秀奖的人数及冠军得主,收集了甲、乙、丙以往的比赛成绩,并整理得到如下数据(单位:m):
)的同学将获得优秀奖.为预测获得优秀奖的人数及冠军得主,收集了甲、乙、丙以往的比赛成绩,并整理得到如下数据(单位:m):甲:9.80,9.70,9.55,9.54,9.48,9.42,9.40,9.35,9.30,9.25;
乙:9.78,9.56,9.51,9.36,9.32,9.23;
丙:9.85,9.65,9.20,9.16.
假设用频率估计概率,且甲、乙、丙的比赛成绩相互独立.
(1)估计甲在校运动会铅球比赛中获得优秀奖的概率;
(2)设X是甲、乙、丙在校运动会铅球比赛中获得优秀奖的总人数,估计X的数学期望E(X);
(3)在校运动会铅球比赛中,甲、乙、丙谁获得冠军的概率估计值最大?(结论不要求证明)
您最近一年使用:0次
2022-06-07更新
|
17179次组卷
|
35卷引用:第07讲 离散型随机变量的分布列与数字特征(练习)
(已下线)第07讲 离散型随机变量的分布列与数字特征(练习)(已下线)考点12 离散型随机变量的期望和方差 2024届高考数学考点总动员(已下线)第3讲:决策的选择问题【练】(已下线)专题21 概率与统计的综合运用(13大题型)(练习)(已下线)专题11 统计与概率(解密讲义)(已下线)题型27 5类概率统计大题综合解题技巧(已下线)专题10.1 概率与统计的综合运用【十一大题型】(举一反三)(新高考专用)-2陕西省西安市蓝田县田家炳中学大学区联考2023-2024学年高二下学期4月阶段性学习效果评测数学试题(已下线)专题25 概率统计解答题(理科)-12022年新高考北京数学高考真题(已下线)2022年新高考北京数学高考真题变式题9-12题(已下线)专题49:离散随机变量的均值与方差-2023届高考数学一轮复习精讲精练(新高考专用)(已下线)6.1 抽样方法及特征数(精练)(已下线)6.7 均值与方差在生活中的运用(精练)(已下线)第07讲 离散型随机变量及其分布列和数字特征 (精讲)(已下线)2022年新高考北京数学高考真题变式题16-18题北京市第八中学2023届高三上学期10月月考数学试题(已下线)考向43 统计与统计案例(九大经典题型)-4(已下线)考向40 事件的相互独立性、条件概率与全概率公式(七大经典题型)-1(已下线)考向38统计与统计案例(重点)-3(已下线)考向42离散型随机变量的期望与方差(重点)-1(已下线)第01讲 统计(练)(已下线)第02讲 概率(练)(已下线)专题9 2022年高考“概率与统计”专题命题分析湖南省永州市江华瑶族自治县第一中学2022-2023学年高三上学期12月月考数学试题(已下线)专题10 概率与统计的综合运用(精讲精练)-1(已下线)第七章 随机变量及其分布 (单元测)(已下线)第七章 随机变量及其分布 全章总结 (精讲)(3)(已下线)重组卷01(已下线)重组卷02(已下线)专题9-1 概率与统计及分布列归类(理)(讲+练)-1(已下线)专题26 概率综合问题(分布列)(解答题)(理科)-3上海市2023届高三考前适应性练习数学试题(已下线)拓展四:近五年随机变量及其分布列高考真题分类汇编 -【帮课堂】2022-2023学年高二数学同步精品讲义(人教A版2019选择性必修第三册)北京十年真题专题11计数原理与概率统计