名校
1 . 某大学就业部从该大学2018年已就业的大学本科毕业生中随机抽取了100人进行了问卷调查,其中有一项是他们的月薪情况,经调查统计发现,他们的月薪收入在3000元到10000元之间,根据统计数据得到如下的频率分布直方图:
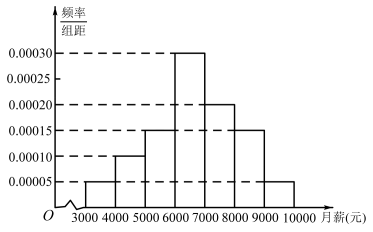
若月薪落在区间 的左侧,则认为该大学本科生属“就业不理想”的学生,学校将联系本人,咨询月薪过低的原因,从而为本科毕业生就业提供更好的指导意见.其中
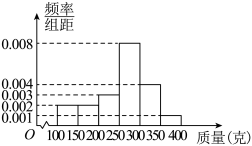
的左侧,则认为该大学本科生属“就业不理想”的学生,学校将联系本人,咨询月薪过低的原因,从而为本科毕业生就业提供更好的指导意见.其中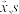 分别为样本平均数和样本标准差,计算可得s≈1500元(同一组中的数据用该组区间的中点值作代表).
分别为样本平均数和样本标准差,计算可得s≈1500元(同一组中的数据用该组区间的中点值作代表).
(1)现该校2018届大学本科毕业生张茗的月薪为3600元,试判断张茗是否属于“就业不理想”的学生?
(2)为感谢同学们对这项调查工作的支持,该校利用分层抽样的方法从样本的前3组中抽出6人,各赠送一份礼品,并从这6人中再抽取2人,各赠送某款智能手机1部,求获赠智能手机的2人中恰有1人月薪不超过5000元的概率;
(3)位于某省的一高校2018届某专业本科毕业生共200人,现他们决定于2019年元旦期间举办一次同学联谊会,并收取一定的活动费用.假定这200人与所抽取样本中的100人月薪分布情况相同,并用样本频率进行估计,现有两种收费方案:
方案一:按每人一个月薪水的10%收取;
方案二:月薪高于样本平均数的每人收取800元,月薪不低于4000元但低于样本平均数的每人收取400元,月薪低于4000元的不收取任何用.
问:哪一种收费方案最终总费用更少?

若月薪落在区间
 的左侧,则认为该大学本科生属“就业不理想”的学生,学校将联系本人,咨询月薪过低的原因,从而为本科毕业生就业提供更好的指导意见.其中
的左侧,则认为该大学本科生属“就业不理想”的学生,学校将联系本人,咨询月薪过低的原因,从而为本科毕业生就业提供更好的指导意见.其中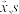 分别为样本平均数和样本标准差,计算可得s≈1500元(同一组中的数据用该组区间的中点值作代表).
分别为样本平均数和样本标准差,计算可得s≈1500元(同一组中的数据用该组区间的中点值作代表).(1)现该校2018届大学本科毕业生张茗的月薪为3600元,试判断张茗是否属于“就业不理想”的学生?
(2)为感谢同学们对这项调查工作的支持,该校利用分层抽样的方法从样本的前3组中抽出6人,各赠送一份礼品,并从这6人中再抽取2人,各赠送某款智能手机1部,求获赠智能手机的2人中恰有1人月薪不超过5000元的概率;
(3)位于某省的一高校2018届某专业本科毕业生共200人,现他们决定于2019年元旦期间举办一次同学联谊会,并收取一定的活动费用.假定这200人与所抽取样本中的100人月薪分布情况相同,并用样本频率进行估计,现有两种收费方案:
方案一:按每人一个月薪水的10%收取;
方案二:月薪高于样本平均数的每人收取800元,月薪不低于4000元但低于样本平均数的每人收取400元,月薪低于4000元的不收取任何用.
问:哪一种收费方案最终总费用更少?
您最近一年使用:0次
2019-05-09更新
|
2186次组卷
|
7卷引用:湖南省长沙市长郡中学2019-2020学年高二上学期第一次模块检测数学试题
名校
2 . 某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量(单位:克)分别在[100,150),[150,200),[200,250),[250,300),[300,350),[350,400]中,经统计得频率分布直方图如图所示.
(1)现按分层抽样的方法从质量为[250,300),[300,350)内的芒果中随机抽取6个,再从这6个中随机抽取3个,求这3个芒果中恰有1个在[300,350)内的概率;
(2)某经销商来收购芒果,以各组数据的中间数代表这组数据的平均值,用样本估计总体,该种植园中还未摘下的芒果大约还有10 000个,经销商提出如下两种收购方案:A方案:所有芒果以10元/千克收购;B方案:对质量低于250克的芒果以2元/个收购,高于或等于250克的以3元/个收购.通过计算确定种植园选择哪种方案获利更多?

(1)现按分层抽样的方法从质量为[250,300),[300,350)内的芒果中随机抽取6个,再从这6个中随机抽取3个,求这3个芒果中恰有1个在[300,350)内的概率;
(2)某经销商来收购芒果,以各组数据的中间数代表这组数据的平均值,用样本估计总体,该种植园中还未摘下的芒果大约还有10 000个,经销商提出如下两种收购方案:A方案:所有芒果以10元/千克收购;B方案:对质量低于250克的芒果以2元/个收购,高于或等于250克的以3元/个收购.通过计算确定种植园选择哪种方案获利更多?
您最近一年使用:0次
2020-06-24更新
|
257次组卷
|
2卷引用:湖南省常德市第二中学2020届高三下学期临考冲刺数学(文)试题
名校
3 . 某校需从甲、乙两名学生中选一人参加物理竞赛,这两名学生最近5次的物理竞赛模拟成绩如下表:
(1)根据成绩的稳定性,现从甲、乙两名学生中选出一人参加物理竞赛,你认为选谁比较合适?
(2)若物理竞赛分为初赛和复赛,在初赛中有如下两种答题方案:方案1:每人从5道备选题中任意抽出1道,若答对,则可参加复赛,否则被淘汰;方案2:每人从5道备选题中任意抽出3道,若至少答对其中2道,则可参加复赛,否则被淘汰.若学生乙只会5道备选题中的3道,则学生乙选择哪种答题方案进入复赛的可能性更大?
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
| 学生甲的成绩(分) | 80 | 85 | 71 | 92 | 87 |
| 学生乙的成绩(分) | 90 | 76 | 75 | 92 | 82 |
(2)若物理竞赛分为初赛和复赛,在初赛中有如下两种答题方案:方案1:每人从5道备选题中任意抽出1道,若答对,则可参加复赛,否则被淘汰;方案2:每人从5道备选题中任意抽出3道,若至少答对其中2道,则可参加复赛,否则被淘汰.若学生乙只会5道备选题中的3道,则学生乙选择哪种答题方案进入复赛的可能性更大?
您最近一年使用:0次
2020-02-15更新
|
324次组卷
|
2卷引用:2020届湖南省长沙市雅礼中学高三第5次月考数学(文)试题
名校
4 . 某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量分别在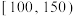 ,
,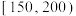 ,
,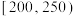 ,
, ,
,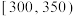 ,
,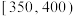 (单位:克)中,经统计得频率分布直方图如图所示.
(单位:克)中,经统计得频率分布直方图如图所示.

(1)经计算估计这组数据的中位数;
(2)现按分层抽样从质量为 ,
,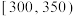 的芒果中随机抽取6个,再从这6个中随机抽取3个,求这3个芒果中恰有1个在
的芒果中随机抽取6个,再从这6个中随机抽取3个,求这3个芒果中恰有1个在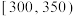 内的概率.
内的概率.
(3)某经销商来收购芒果,以各组数据的中间数代表这组数据的平均值,用样本估计总体,该种植园中还未摘下的芒果大约还有10000个,经销商提出如下两种收购方案:
A:所有芒果以10元/千克收购;
B:对质量低于250克的芒果以2元/个收购,高于或等于250克的以3元/个收购,通过计算确定种植园选择哪种方案获利更多?
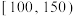 ,
,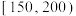 ,
,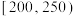 ,
, ,
,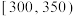 ,
,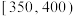 (单位:克)中,经统计得频率分布直方图如图所示.
(单位:克)中,经统计得频率分布直方图如图所示.
(1)经计算估计这组数据的中位数;
(2)现按分层抽样从质量为
 ,
,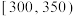 的芒果中随机抽取6个,再从这6个中随机抽取3个,求这3个芒果中恰有1个在
的芒果中随机抽取6个,再从这6个中随机抽取3个,求这3个芒果中恰有1个在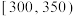 内的概率.
内的概率.(3)某经销商来收购芒果,以各组数据的中间数代表这组数据的平均值,用样本估计总体,该种植园中还未摘下的芒果大约还有10000个,经销商提出如下两种收购方案:
A:所有芒果以10元/千克收购;
B:对质量低于250克的芒果以2元/个收购,高于或等于250克的以3元/个收购,通过计算确定种植园选择哪种方案获利更多?
您最近一年使用:0次
2020-01-10更新
|
1306次组卷
|
17卷引用:吉林省长春市普通高中2018届高三质量监测(二)数学(文)试题
吉林省长春市普通高中2018届高三质量监测(二)数学(文)试题【全国市级联考】陕西省延安市2018届高三高考模拟文科数学试题【全国百强校】郑州外国语学校2018届高三第十五次调研考试(文)试题【市级联考】吉林省长春市2018届高三高考二模数学试题(文科)【市级联考】广东省潮州市2019届高三上学期期末教学质量检测数学(文)试题【市级联考】辽宁省沈阳市郊联体2019届高三第一次模拟考试数学(理科)试题【全国百强校】河北省唐山市第一中学2019届高三下学期冲刺(二)数学(文)试题辽宁省沈阳市郊联体2018-2019学年高一下学期期末数学试题河北省保定七校2019-2020学年高三上学期第三次联考文数试题山西省长治市2019届高三下学期3月统一联合考试数学(文)试题2020届吉林省白城四中高三网上模拟考数学文科试题2020届甘肃省天水市第一中学高三下学期诊断考试数学(文)试题湖南省长沙市宁乡市2021-2022学年高二下学期期末数学试题陕西省西安中学2021届高三下学期第四次模拟数学(文)试题(已下线)福建省厦门市集美中学2020-2021学年高一下学期期末数学试题河北省尚义县第一中学2020-2021学年高二下学期期中数学试题黑龙江省大庆铁人中学2021-2022学年高二下学期第一次月考数学试题
名校
5 . 依据黄河济南段8月份的水文观测点的历史统计数据所绘制的频率分布直方图如图(甲)所示:依据济南的地质构造,得到水位与灾害等级的频率分布条形图如图(乙)所示.
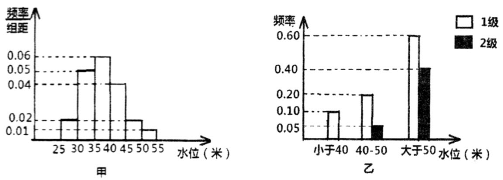
(I)以此频率作为概率,试估计黄河济南段在8月份发生I级灾害的概率;
(Ⅱ)黄河济南段某企业,在8月份,若没受1、2级灾害影响,利润为500万元;若受1级灾害影响,则亏损100万元;若受2级灾害影响则亏损1000万元.
现此企业有如下三种应对方案:

试问,如仅从利润考虑,该企业应选择这三种方案中的哪种方案?说明理由.

(I)以此频率作为概率,试估计黄河济南段在8月份发生I级灾害的概率;
(Ⅱ)黄河济南段某企业,在8月份,若没受1、2级灾害影响,利润为500万元;若受1级灾害影响,则亏损100万元;若受2级灾害影响则亏损1000万元.
现此企业有如下三种应对方案:

试问,如仅从利润考虑,该企业应选择这三种方案中的哪种方案?说明理由.
您最近一年使用:0次
2018-12-05更新
|
660次组卷
|
11卷引用:湖南省长沙市第一中学2018-2019学年高三下学期第九次月考数学(理)试题
湖南省长沙市第一中学2018-2019学年高三下学期第九次月考数学(理)试题广东省深中、华附、省实、广雅四校2018届高三模拟联考理科数学试题(已下线)2018年高考数学备考中等生百日捷进提升系列(综合提升篇) 专题02 概率统计解答题(理)【全国百强校】山东省实验中学2019届高三第二次诊断性考试数学(理)试题河北省沧州市第一中学2019-2020学年高二下学期空中课堂3月阶段测试数学试题广东省深圳外国语学校2019-2020学年高三下学期4月月考数学(理)试题河北省鸡泽县第一中学2019-2020学年高二下学期开学考试数学试题四川省内江市第六中学2020届高三热身考试数学(理)试题(已下线)综合练习模拟卷02-2021年高考一轮数学单元复习一遍过(新高考地区专用)(已下线)综合练习模拟卷02-2021年高考一轮数学(理)单元复习一遍过人教A版(2019) 选修第三册 过关斩将 第七章 7.1~7.3综合拔高练
名校
6 . 某商场周年庆,准备提供一笔资金,对消费满一定金额的顾客以参与活动的方式进行奖励.顾客从一个装有大小相同的2个红球和4个黄球的袋中按指定规则取出2个球,根据取到的红球数确定奖励金额,具体金额设置如下表:
现有两种取球规则的方案:
方案一:一次性随机取出2个球;
方案二:依次有放回取出2个球.
(Ⅰ)比较两种方案下,一次抽奖获得50元奖金概率的大小;
(Ⅱ)为使得尽可能多的人参与活动,作为公司的负责,你会选择哪种方案?请说明理由.
取到的红球数 | 0 | 1 | 2 |
奖励(单位:元) | 5 | 10 | 50 |
方案一:一次性随机取出2个球;
方案二:依次有放回取出2个球.
(Ⅰ)比较两种方案下,一次抽奖获得50元奖金概率的大小;
(Ⅱ)为使得尽可能多的人参与活动,作为公司的负责,你会选择哪种方案?请说明理由.
您最近一年使用:0次
2017-08-22更新
|
756次组卷
|
2卷引用:湖南省长沙市长郡中学2018届高三第一次暑假作业检测数学(理)试题
名校
解题方法
7 . 某展会安排了分别标有序号为“1号”“2号”“3号”的三辆车,等可能的随机顺序前往酒店接嘉宾,某嘉宾突发奇想,设计了两种乘车方案.方案一:不乘坐第一辆车,若第二辆车的车序号大于第一辆车的车序号,就乘坐此车,否则乘坐第三辆车;方案二:直接乘坐第一辆车.记方案一与方案二坐到“3号”车的概率分别为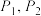 ,则( )
,则( )
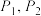 ,则( )
,则( )A.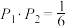 | B.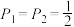 |
C.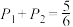 | D. |
您最近一年使用:0次
2023-08-23更新
|
435次组卷
|
9卷引用:江苏省苏州市吴中联考2019-2020学年高一下学期期中数学试题
江苏省苏州市吴中联考2019-2020学年高一下学期期中数学试题湖南省长沙市雅礼中学2021-2022学年高二上学期入学考试数学试题(已下线)10.1 随机事件与概率 2020--2021高中数学新教材配套提升训练(人教A版必修第二册)(已下线)黄金卷20-【赢在高考·黄金20卷】备战2021年高考数学全真模拟卷(山东高考专用)湖北省荆州市沙市中学2021-2022学年高二上学期期中数学试题湖北省黄冈市黄州中学2021-2022学年高二上学期新起点开学考试数学试题云南省大理市大理白族自治州民族中学2023-2024学年高二上学期开学考试数学试题北师大版(2019) 必修第一册 章末检测卷(七)概率湖北省黄冈市黄梅国际育才高级中学2023-2024学年高二上学期9月月考数学试题
名校
解题方法
8 . 某校为举办甲、乙两项不同活动,分别设计了相应的活动方案:方案一、方案二.为了解该校学生对活动方案是否支持,对学生进行简单随机抽样,获得数据如下表:
假设所有学生对活动方案是否支持相互独立.
(1)分别估计该校男生支持方案一的概率、该校女生支持方案一的概率;
(2)从该校全体男生中随机抽取2人,全体女生中随机抽取1人,估计这3人中恰有2人支持方案一的概率.
| 男生 | 女生 | |||
| 支持 | 不支持 | 支持 | 不支持 | |
| 方案一 | 200人 | 400人 | 300人 | 100人 |
| 方案二 | 350人 | 250人 | 150人 | 250人 |
(1)分别估计该校男生支持方案一的概率、该校女生支持方案一的概率;
(2)从该校全体男生中随机抽取2人,全体女生中随机抽取1人,估计这3人中恰有2人支持方案一的概率.
您最近一年使用:0次
2022-07-22更新
|
238次组卷
|
6卷引用:沪教版(2020) 25天高考冲刺 双新双基百分百13
2013·山西·模拟预测
名校
解题方法
9 . 某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与医院抄录1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数,得到如下图资料:
该兴趣小组的研究方案是先从这6组数据中选取2组,用剩下的4组数据求线性回归方程,再用被选取的2组数据检验.
(1)求选取的2组数据恰好相邻的概率;
(2)若选取的是1月与6月的两组数据,请根据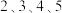 月份的数据,求出y关于x的线性回归方程
月份的数据,求出y关于x的线性回归方程 ;
;
(3)若线性回归方程得出的估计数据与所选出的检验数据误差的绝对值都不超过2,则认为得到的线性回归方程是理想的.试问该小组由(2)中得到的线性回归方程是否理想?
附: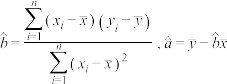 .
.
| 日期 | 1月10日 | 2月10日 | 3月10日 | 4月10日 | 5月10日 | 6月10日 |
昼夜温差 | 10 | 11 | 13 | 12 | 8 | 6 |
| 就诊人数y(个) | 22 | 25 | 29 | 26 | 16 | 12 |
(1)求选取的2组数据恰好相邻的概率;
(2)若选取的是1月与6月的两组数据,请根据
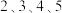 月份的数据,求出y关于x的线性回归方程
月份的数据,求出y关于x的线性回归方程 ;
;(3)若线性回归方程得出的估计数据与所选出的检验数据误差的绝对值都不超过2,则认为得到的线性回归方程是理想的.试问该小组由(2)中得到的线性回归方程是否理想?
附:
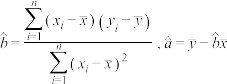 .
.
您最近一年使用:0次
2021-05-10更新
|
911次组卷
|
24卷引用:2016届湖南长沙市雅礼中学高三月考八数学(文)试卷
2016届湖南长沙市雅礼中学高三月考八数学(文)试卷湖南省长沙市长郡中学2018届高三月考试题(二)数学(理科)试题湖南省浏阳一中、株洲二中等湘东五校2018届高三12月联考数学(文)试题湖南省长沙市长郡中学2017-2018学年高二12月月考(第二次模块检测)数学(文)试题(已下线)2013届山西省康杰中学高三第八次模拟文科数学试卷2015届宁夏银川一中高三第一次模拟考试文科数学试卷2014-2015学年黑龙江哈尔滨师大附中高二上学期期末考试理科数学卷2016届海南省海南中学高三考前模拟十二理科数学试卷2016届海南省海南中学高三考前模拟十二文科数学试卷2016-2017学年河北枣强中学高二上期中数学(理)试卷2016-2017学年河北枣强中学高二上期中数学(文)试卷宁夏银川一中2016-2017学年高二下学期期末考试数学(理)试题吉林省吉林大学附属中学2017届高三第六次摸底考试数学(理)试题内蒙古赤峰二中2016-2017学年高二下学期第二次月考数学(理)试题四川省棠湖中学2017-2018学年高二下学期开学考试数学(理)试题【全国市级联考】河南省南阳市2017-2018学年高一下学期期中考试数学试题【全国百强校】河南省南阳市第一中学2017-2018学年高二下学期第三次月考数学(文)试题【全国百强校】山东省淄博市高青县第一中学2017-2018学年高一下学期期末模块检测数学试题【市级联考】湖北省黄冈市2019届高三八模模拟测试卷(二)文科数学试题【全国百强校】安徽省蚌埠市第二中学2018-2019学年高二下学期期中考试数学(文)试题2020届大象联考河南省普通高中高考质量测评(一)数学文科试题贵州省贵阳市2021届高三二模数学(文)试题贵州省贵阳市2021届高三二模数学(理)试题四川省仁寿第一中学校南校区2020-2021学年高二5月第二次质量检测数学(理)试题
2014·广东惠州·二模
名校
解题方法
10 . 移动公司在国庆期间推出 套餐,对国庆节当日办理套餐的客户进行优惠,优惠方案如下:选择套餐1的客户可获得优惠
套餐,对国庆节当日办理套餐的客户进行优惠,优惠方案如下:选择套餐1的客户可获得优惠 元,选择套餐2的客户可获得优惠
元,选择套餐2的客户可获得优惠 元,选择套餐3的客户可获得优惠
元,选择套餐3的客户可获得优惠 元.国庆节当天参与活动的人数统计结果如图所示,现将频率视为概率.
元.国庆节当天参与活动的人数统计结果如图所示,现将频率视为概率.
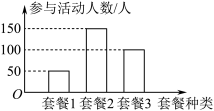
(1)求从中任选1人获得优惠金额不低于300元的概率;
(2)若采用分层抽样的方式从参加活动的客户中选出6人,再从该6人中随机选出2人,求这2人获得相等优惠金额的概率.
 套餐,对国庆节当日办理套餐的客户进行优惠,优惠方案如下:选择套餐1的客户可获得优惠
套餐,对国庆节当日办理套餐的客户进行优惠,优惠方案如下:选择套餐1的客户可获得优惠 元,选择套餐2的客户可获得优惠
元,选择套餐2的客户可获得优惠 元,选择套餐3的客户可获得优惠
元,选择套餐3的客户可获得优惠 元.国庆节当天参与活动的人数统计结果如图所示,现将频率视为概率.
元.国庆节当天参与活动的人数统计结果如图所示,现将频率视为概率.
(1)求从中任选1人获得优惠金额不低于300元的概率;
(2)若采用分层抽样的方式从参加活动的客户中选出6人,再从该6人中随机选出2人,求这2人获得相等优惠金额的概率.
您最近一年使用:0次
2021-01-08更新
|
521次组卷
|
7卷引用:2015届广东惠州市高三第二次调研考试文科数学试卷
(已下线)2015届广东惠州市高三第二次调研考试文科数学试卷2015-2016学年河北武邑中学高二上1.17周考文数学卷2017届宁夏中卫一中高三上周练一数学(文)试卷贵州黔东南州2017届高三高考第一次模拟考试文科数学试题(已下线)专题11.3 概率单元检测-2021届高考数学(文)一轮复习讲练测贵州省毕节市七星关区海子街中学2018-2019学年高二下学期期末考试数学(文)试题湖南省长沙市第一中学2023-2024学年高二上学期第一阶段性检测数学试题



