1 . 某地经过多年的环境治理,已将荒山改造成了绿水青山,为估计一林区某种树木的总材积量.随机选取了10棵这种树木,测量每棵树的根部横截面积(单位: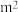 )和材积量(单位:
)和材积量(单位: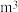 ),得到如下数据:
),得到如下数据:
并计算得 .
.
(1)估计该林区这种树木平均一棵的根部横截面积与平均一棵的材积量;
(2)求该林区这种树木的根部横截面积与材积量的样本相关系数(精确到0.01).
附:相关系数 ,
,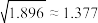 .
.
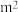 )和材积量(单位:
)和材积量(单位: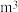 ),得到如下数据:
),得到如下数据:| 样本号i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 总和 |
根部横截面积 | 0.04 | 0.06 | 0.04 | 0.03 | 0.08 | 0.05 | 0.05 | 0.07 | 0.07 | 0.06 | 0.6 |
材积量 | 0.25 | 0.40 | 0.22 | 0.54 | 0.51 | 0.34 | 0.36 | 0.46 | 0.42 | 0.40 | 3.9 |
 .
.(1)估计该林区这种树木平均一棵的根部横截面积与平均一棵的材积量;
(2)求该林区这种树木的根部横截面积与材积量的样本相关系数(精确到0.01).
附:相关系数
 ,
,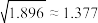 .
.
您最近一年使用:0次
2024-04-04更新
|
647次组卷
|
6卷引用:河南省灵宝市第三高级中学2023-2024学年高二下学期精英对抗赛数学试题
河南省灵宝市第三高级中学2023-2024学年高二下学期精英对抗赛数学试题陕西师范大学附属中学2023-2024学年高二下学期第一次月考数学试题(已下线)专题8.7 成对数据的统计分析全章综合测试卷(基础篇)-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)(已下线)8.1 成对数据的统计相关性(4大题型)精讲-2023-2024学年高二数学题型分类归纳讲与练(人教A版2019选择性必修第三册)(已下线)第八章:成对数据的统计分析章末综合检测卷(新题型)-2023-2024学年高二数学题型分类归纳讲与练(人教A版2019选择性必修第三册)(已下线)专题4.1 数据的相关性及回归方程(八个重难点突破)-2023-2024学年高二数学下学期重难点突破及混淆易错规避(人教A版2019)
2 . 如果将一组数据5、4、6、5、4、13、5依次重复写10次,会得到70个数组成的一组新数据,关于这组新数据的中位数、众数、平均数,下列说法正确的是( )
| A.中位数和众数都是5 | B.众数是10 |
| C.中位数是4 | D.中位数、平均数都是5 |
您最近一年使用:0次
2024-01-26更新
|
418次组卷
|
9卷引用:湖南省邵阳市2023-2024学年高一上学期拔尖创新人才早期培养竞赛(初赛)数学试题
湖南省邵阳市2023-2024学年高一上学期拔尖创新人才早期培养竞赛(初赛)数学试题(已下线)专题9.2 用样本估计总体-举一反三系列(人教A版2019必修第二册)(已下线)9.2.3?总体集中趋势的估计——课后作业(基础版)(已下线)14.4 用样本估计总体(1)-【帮课堂】(苏教版2019必修第二册)(已下线)专题22 用样本估计总体-《重难点题型·高分突破》(人教A版2019必修第二册)(已下线)专题23 统计图表 用样本估计总体-《重难点题型·高分突破》(苏教版2019必修第二册)(已下线)第07讲 第九章 统计 章末重点题型大总结-【帮课堂】(人教A版2019必修第二册)(已下线)第05讲 9.2.3 总体集中趋势的估计-【帮课堂】(人教A版2019必修第二册)【巩固卷】第6章 统计学初步 素养检测 单元测试A-湘教版(2019)必修(第一册)
名校
3 . 为了增强学生的国防意识,某中学组织了一次国防知识竞赛,高一和高二两个年级学生参加知识竞赛,
(1)两个年级各派50名学生参加国防知识初赛,成绩均在区间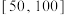 上,现将成绩制成如图所示频率分布直方图(每组均包括左端点,最后一组包括右端点),估计学生的成绩的平均分(若同一组中的数据用该组区间的中点值为代表);
上,现将成绩制成如图所示频率分布直方图(每组均包括左端点,最后一组包括右端点),估计学生的成绩的平均分(若同一组中的数据用该组区间的中点值为代表);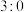 ,则不需再答第4轮了;③设高一年级的学生代表甲答对比赛题目的概率是
,则不需再答第4轮了;③设高一年级的学生代表甲答对比赛题目的概率是 ,高二年级的学生代表乙答对比赛题目的概率是
,高二年级的学生代表乙答对比赛题目的概率是 ,每轮答题比赛中,答对与否互不影响,各轮结果也互不影响
,每轮答题比赛中,答对与否互不影响,各轮结果也互不影响
(i)在一次赛前训练中,学生代表甲同学答了3轮题,且每次答题互不影响,记 为答对题目的数量,求
为答对题目的数量,求 的分布列及数学期望
的分布列及数学期望
(ii)求在第4轮结束时,学生代表甲答对3道题并刚好胜出的概率
(1)两个年级各派50名学生参加国防知识初赛,成绩均在区间
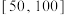 上,现将成绩制成如图所示频率分布直方图(每组均包括左端点,最后一组包括右端点),估计学生的成绩的平均分(若同一组中的数据用该组区间的中点值为代表);
上,现将成绩制成如图所示频率分布直方图(每组均包括左端点,最后一组包括右端点),估计学生的成绩的平均分(若同一组中的数据用该组区间的中点值为代表);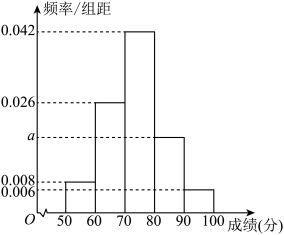
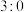 ,则不需再答第4轮了;③设高一年级的学生代表甲答对比赛题目的概率是
,则不需再答第4轮了;③设高一年级的学生代表甲答对比赛题目的概率是 ,高二年级的学生代表乙答对比赛题目的概率是
,高二年级的学生代表乙答对比赛题目的概率是 ,每轮答题比赛中,答对与否互不影响,各轮结果也互不影响
,每轮答题比赛中,答对与否互不影响,各轮结果也互不影响(i)在一次赛前训练中,学生代表甲同学答了3轮题,且每次答题互不影响,记
 为答对题目的数量,求
为答对题目的数量,求 的分布列及数学期望
的分布列及数学期望(ii)求在第4轮结束时,学生代表甲答对3道题并刚好胜出的概率
您最近一年使用:0次
2023-02-10更新
|
1264次组卷
|
8卷引用:安徽省安庆市田家炳中学2022-2023学年高二下学期第二届“校长杯”竞赛数学试题
名校
解题方法
4 . 某大学为了解学生对 两家餐厅的满意度情况,从在
两家餐厅的满意度情况,从在 两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行满意指数打分(满意指数是指学生对餐厅满意度情况的打分,分数设置为
两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行满意指数打分(满意指数是指学生对餐厅满意度情况的打分,分数设置为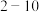 分
分 .根据打分结果按
.根据打分结果按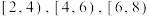 ,
, 分组,得到如图所示的频率分布直方图,其中
分组,得到如图所示的频率分布直方图,其中 餐厅满意指数在
餐厅满意指数在 中有30人.
中有30人. 餐厅满意指数频率分布直方图中
餐厅满意指数频率分布直方图中 的值;
的值;
(2)利用样本估计总体的思想,估计 餐厅满意指数和
餐厅满意指数和 餐厅满意指数的平均数及方差(同一组中的数据用该组区间中点值作代表);
餐厅满意指数的平均数及方差(同一组中的数据用该组区间中点值作代表);
参考公式: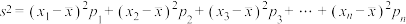 ,其中
,其中 为
为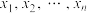 的平均数,
的平均数,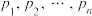 分别为
分别为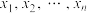 对应的频率.
对应的频率.
(3)如果一名新来同学打算从 两家餐厅中选择一个用餐,你建议选择哪个餐厅?说明理由.
两家餐厅中选择一个用餐,你建议选择哪个餐厅?说明理由.
 两家餐厅的满意度情况,从在
两家餐厅的满意度情况,从在 两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行满意指数打分(满意指数是指学生对餐厅满意度情况的打分,分数设置为
两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行满意指数打分(满意指数是指学生对餐厅满意度情况的打分,分数设置为 分
分 .根据打分结果按
.根据打分结果按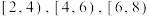 ,
, 分组,得到如图所示的频率分布直方图,其中
分组,得到如图所示的频率分布直方图,其中 餐厅满意指数在
餐厅满意指数在 中有30人.
中有30人.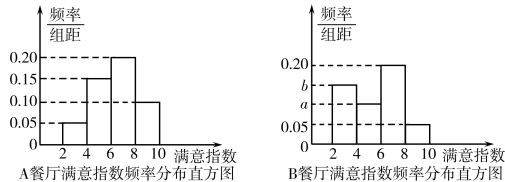
 餐厅满意指数频率分布直方图中
餐厅满意指数频率分布直方图中 的值;
的值;(2)利用样本估计总体的思想,估计
 餐厅满意指数和
餐厅满意指数和 餐厅满意指数的平均数及方差(同一组中的数据用该组区间中点值作代表);
餐厅满意指数的平均数及方差(同一组中的数据用该组区间中点值作代表);参考公式:
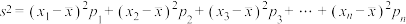 ,其中
,其中 为
为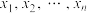 的平均数,
的平均数,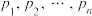 分别为
分别为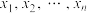 对应的频率.
对应的频率.(3)如果一名新来同学打算从
 两家餐厅中选择一个用餐,你建议选择哪个餐厅?说明理由.
两家餐厅中选择一个用餐,你建议选择哪个餐厅?说明理由.
您最近一年使用:0次
2022-01-19更新
|
1424次组卷
|
7卷引用:山东省高密市第一中学2023-2024学年高一上学期冬学竞赛数学试题
山东省高密市第一中学2023-2024学年高一上学期冬学竞赛数学试题山东省潍坊市2021-2022学年高一上学期期末数学试题(已下线)9.2 用样本估计总体~9.3 统计案例 公司员工的肥胖情况调查分析-2021-2022学年高一数学10分钟课前预习练(人教A版2019必修第二册)吉林省吉林市吉化第一高级中学校2021-2022学年高一下学期期中考试数学试题(已下线)第13讲 用样本估计总体(核心考点讲与练)-2021-2022学年高一数学考试满分全攻略(人教A版2019必修第二册)(已下线)9.3 统计案例 公司员工的肥胖情况调查分析(分层作业)-【上好课】河南省三门峡市2023-2024学年高一下学期期末调研考试数学试题
13-14高二上·湖北武汉·期末
名校
5 . 某人5次上班途中所花的时间(单位:分钟)分别为x,y,10,11,9.已知这组数据的平均数为10,方差为2,则|x﹣y|的值为_____ .
您最近一年使用:0次
2019-06-24更新
|
4231次组卷
|
42卷引用:第十一届高二试题(A卷)-“枫叶新希望杯”全国数学大赛真题解析(高中版)
第十一届高二试题(A卷)-“枫叶新希望杯”全国数学大赛真题解析(高中版)(已下线)2012-2013学年湖北武汉部分重点中学高二上学期期末考试文科数学卷(已下线)2012-2013学年安徽省周集中学高二上学期期中考试文科数学试卷(已下线)2014届上海市徐汇区高三上学期期末考试(一模)理科数学试卷(已下线)2014届上海市徐汇区高三上学期期末考试(一模)文科数学试卷(已下线)2013-2014学年湖北荆门市高二上学期期末质量检测文数学试卷(已下线)2013-2014学年福建省福州第八中学高二下学期期中考试文科数学试卷2015-2016学年山西省怀仁县一中高一12月月考数学试卷2015-2016学年江苏省泰兴中学高二下学期期中数学(理)试卷吉林省辽源第五中学2016-2017学年高二下学期期末考试数学(文)试题四川省成都市第七中学2019届高三二诊数学(文)模拟考试试题四川省成都市第七中学2019届高三二诊数学(理)模拟考试试题【校级联考】广西玉林市2018-2019学年高二下学期四校(玉林一中、北流高中、容县高中、陆川中学)联考文科数学试题人教B版(2019) 必修第二册 过关斩将 第五章 5.1 统计 5.1.2 数据的数字特征上海市位育中学2018-2019学年高二下学期期末数学试题上海市复旦大学附属中学2019-2020学年高三上学期开学摸底数学试题(已下线)专题10.2 用样本估计总体(练)【文】-《2020年高考一轮复习讲练测》人教A版(2019) 必修第二册 逆袭之路 第九章 统计 本章整合提升上海市控江中学2017届高三上学期开学摸底考试数学试题人教A版(2019) 必修第二册 必杀技 第9章 9.2.4总体离散程度的估计黑龙江省伊春市第二中学2019-2020学年高二上学期期末数学(文)试题黑龙江省伊春市第二中学2019-2020学年高二上学期期末数学(理)试题(已下线)狂刷52 统计及统计案例-学易试题君之小题狂刷2020年高考数学(理)2020届上海市高三押题卷一数学试题上海市建平中学2021届高三上学期9月月考数学试题山东省青岛市胶州市实验中学2019-2020学年第二学期高一数学期中模拟检测(二)湖北省武汉市华师一附中2020-2021学年高二上学期期中数学试题广东省部分重点学校2020-2021学年高一下学期期末数学试题上海市浦东新区浦东中学2021届高三上学期10月月考数学试题(已下线)9.2用样本估计总体A卷重庆市南华中学校2021-2022学年高二上学期开学考试数学试题沪教版(2020) 必修第三册 精准辅导 第13章 13.5(2) 估计总体的数字特征苏教版(2019) 必修第二册 必杀技 第14章 统计 14.4 用样本估计总体 14.4.2 用样本估计总体的离散程度参数第13章 统计(B卷·能力提升练)-【单元测试】2022-2023学年高二数学分层训练AB卷(沪教版2020必修第三册)6.4.1样本的数字特征 同步练习-2021-2022学年高一上学期数学北师大版(2019)必修第一册6.4.1样本的数字特征-2020-2021学年高一数学北师大版2019必修第一册内蒙古赤峰二中2022-2023学年高二下学期第一次月考数学(文)试题(已下线)模块三 专题1 小题入门夯实练 (2)(人教A)江苏省常州高级中学2022-2023学年高一下学期期末数学试题(已下线)模块三 专题1 小题入门夯实练 (2)(苏教版)湖北省部分省级示范高中2023~2024学年高一下学期期末测试数学试卷四川省内江市第一中学2022-2023学年高二上学期期中考试数学试题
名校
6 . 从甲、乙两名学生中选拔一人参加射箭比赛,为此需要对他们的射箭水平进行测试.现这两名学生在相同条件下各射箭10次,命中的环数如下:
(1)计算甲、乙两人射箭命中环数的平均数和标准差;
(2)比较两个人的成绩,然后决定选择哪名学生参加射箭比赛.
甲 | 8 | 9 | 7 | 9 | 7 | 6 | 10 | 10 | 8 | 6 |
乙 | 10 | 9 | 8 | 6 | 8 | 7 | 9 | 7 | 8 | 8 |
(2)比较两个人的成绩,然后决定选择哪名学生参加射箭比赛.
您最近一年使用:0次
2016-12-03更新
|
510次组卷
|
8卷引用:2015-2016学年河北省定州市李亲顾中学高二上学期竞赛数学试卷
2015-2016学年河北省定州市李亲顾中学高二上学期竞赛数学试卷2016-2017学年福建莆田二十四中高二文上学期期中考数学试卷陕西省黄陵中学2017-2018学年高二(重点班)上学期期末考试数学试题吉林省辽源市田家炳高级中学2017-2018学年高二下学期3月月考数学(文)试题河北省衡水市武邑中学2017-2018学年高二下学期期末考试数学(文)试题西藏自治区日喀则市南木林高级中学2019-2020学年高一下学期期中考试数学试题广西靖西市第二中学2020-2021学年高二10月月考数学试题(已下线)9.2.3 总体集中趋势的估计 9.2.4 总体离散程度的估计(分层练习)-2020-2021学年高一数学新教材配套练习(人教A版2019必修第二册)
9-10高一下·陕西延安·期末
名校
7 . 已知样本 的平均数是
的平均数是 ,标准差是
,标准差是 ,则
,则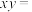
________ .
 的平均数是
的平均数是 ,标准差是
,标准差是 ,则
,则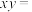
您最近一年使用:0次
2016-12-02更新
|
1826次组卷
|
26卷引用:第八届高二试题(A卷)-“枫叶新希望杯”全国数学大赛真题解析(高中版)
第八届高二试题(A卷)-“枫叶新希望杯”全国数学大赛真题解析(高中版)(已下线)2010年延安市实验中学高一下学期期末考试数学卷(已下线)2010年河北省南宫中学高二12月月考数学卷(已下线)2011-2012学年内蒙古包头三十三中高二上学期期末文科数学试卷(已下线)2012-2013学年广东省深圳高级中学高二第二学期期中考试数学理试卷(已下线)2013-2014学年河南长葛第三实验高中高一下学期第三次考试数学试卷(已下线)2013-2014学年河南省开封实验学校高一下学期期末练习2数学试卷(已下线)2013-2014学年河南省开封高中实验学校高一下学期期末数学试卷2(已下线)2014-2015学年宁夏育才中学高二上学期第一次月考理科数学试卷(已下线)2014-2015学年宁夏育才中学高二上学期第一次月考文科数学试卷2015-2016学年湖南长郡中学高二水平模拟理科数学卷2016-2017学年湖北大冶市实验中学高二上学期月考一数学试卷江苏省南京市金陵中学2015-2016学年高二下学期期中复习数学试题【市级联考】河南省南阳市2018-2019学年高一下学期期中考试数学试题【全国百强校】江苏省泰州中学2018-2019学年高二下学期期中考试数学(文)试题江苏省泰州市泰州中学2018-2019学年高二下学期期中考试数学(理)试题人教A版(2019) 必修第二册 逆袭之路 第九章 9.2 用样本估计总体 9.2.4 总体离散程度的估计安徽省铜陵市第一中学2018-2019学年高二上学期期中数学试题(已下线)专题16 用样本估计总体、统计案例(核心素养练习)-【新教材精创】2019-2020高一数学新教材知识讲学(人教A版必修第二册)-《高中新教材知识讲学》山东省菏泽市第一中学八一路校区2019-2020学年高一6月月考数学试题四川省眉山市东坡区永寿高级中学2019-2020学年高二下学期期中考试数学(文)试题专题5.3 统计与概率(A卷基础篇)-2020-2021学年高一数学必修第二册同步单元AB卷(新教材人教B版)沪教版(2020) 必修第三册 新课改一课一练 第13章 13.5.2估计总体的数字特征苏教版(2019) 必修第二册 一课一练 第14章 统计 14.4 用样本估计总体 第2课时 用样本估计总体的离散程度参数上海市上南中学2021-2022学年高二上学期期末数学试题【课堂练】 13.5.2 估计总体的数字特征 随堂练习-沪教版(2020)必修第三册 第13章 统计



