名校
1 . 某企业新研发了一种产品,产品的成本由原料成本及非原料成本组成,每件产品的非原料成本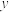 (元)与生产的产品数量
(元)与生产的产品数量 (千件)有关,经统计得到如下数据:
(千件)有关,经统计得到如下数据:
(1)根据表中的数据,运用相关系数进行分析说明,是否可以用线性回归模型拟合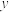 与
与 的关系?并指出是正相关还是负相关;
的关系?并指出是正相关还是负相关;
(2)求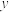 关于
关于 的回归方程,并预测生产该产品13千件时,每件产品的非原料成本为多少元?
的回归方程,并预测生产该产品13千件时,每件产品的非原料成本为多少元?
(3)设 满足
满足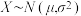 ,其中
,其中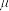 近似为样本平均数
近似为样本平均数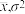 近似为样本方差
近似为样本方差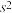 ,求
,求 .
.
附:参考公式:相关系数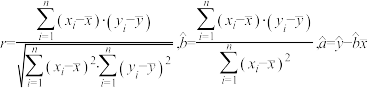 ;
;
参考数据: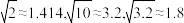 ,若
,若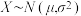 ,则
,则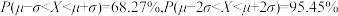 .
.
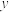 (元)与生产的产品数量
(元)与生产的产品数量 (千件)有关,经统计得到如下数据:
(千件)有关,经统计得到如下数据: | 2 | 5 | 8 | 9 | 11 |
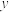 | 12 | 10 | 8 | 8 | 7 |
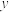 与
与 的关系?并指出是正相关还是负相关;
的关系?并指出是正相关还是负相关;(2)求
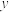 关于
关于 的回归方程,并预测生产该产品13千件时,每件产品的非原料成本为多少元?
的回归方程,并预测生产该产品13千件时,每件产品的非原料成本为多少元?(3)设
 满足
满足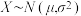 ,其中
,其中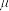 近似为样本平均数
近似为样本平均数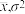 近似为样本方差
近似为样本方差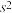 ,求
,求 .
.附:参考公式:相关系数
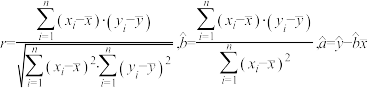 ;
;参考数据:
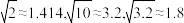 ,若
,若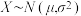 ,则
,则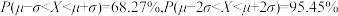 .
.
您最近半年使用:0次
2022-10-25更新
|
519次组卷
|
2卷引用:贵州省黔东南州凯里市第一中学2023届高三上学期第四次月考数学(理)试题
名校
解题方法
2 . 下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量 (吨)与相应的生产能耗
(吨)与相应的生产能耗 (吨标准煤)的几组对照数据.
(吨标准煤)的几组对照数据.
(1)请根据表中提供的数据,求出 关于
关于 的线性回归方程;
的线性回归方程;
(2)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(1)求出的线性回归方程预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
参考公式: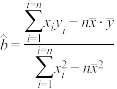 ;
; .
.
 (吨)与相应的生产能耗
(吨)与相应的生产能耗 (吨标准煤)的几组对照数据.
(吨标准煤)的几组对照数据. | 3 | 4 | 5 | 6 |
 | 2.5 | 3 | 4 | 4.5 |
 关于
关于 的线性回归方程;
的线性回归方程;(2)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(1)求出的线性回归方程预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
参考公式:
 ;
; .
.
您最近半年使用:0次
2022-07-25更新
|
123次组卷
|
7卷引用:贵州省毕节市金沙县第五中学2021-2022学年高二上学期第一次月考数学试题
解题方法
3 . 一位父亲在孩子出生后,每月给小孩测量一次身高,得到前7个月的数据如下表所示.
(1)求小孩前7个月的平均身高;
(2)求出身高y关于月龄x的回归直线方程(计算结果精确到整数部分);
(3)利用(2)的结论预测一下8个月的时候小孩的身高.
参考公式: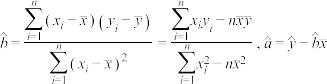 .
.
月龄 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
身高(单位:厘米) | 52 | 56 | 60 | 63 | 65 | 68 | 70 |
(2)求出身高y关于月龄x的回归直线方程(计算结果精确到整数部分);
(3)利用(2)的结论预测一下8个月的时候小孩的身高.
参考公式:
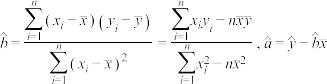 .
.
您最近半年使用:0次
2022-07-05更新
|
227次组卷
|
2卷引用:贵州省六盘水第五中学2021-2022学年高二上学期期末数学试题
名校
解题方法
4 . 下表是某学生在4月份开始进入冲刺复习至高考前的5次大型联考数学成绩(分):
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程;
(2)若在4月份开始进入冲刺复习前,该生的数学分数最好为116分,并以此作为初始分数,利用上述回归方程预测高考的数学成绩,并以预测高考成绩作为最终成绩,求该生4月份后复习提高率. (复习提高率=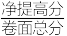 ×100%,分数取整数).
×100%,分数取整数).
附:回归直线的斜率和截距的最小二乘估计公式分别为: ,
, ,其中
,其中 为样本平均值,
为样本平均值,
线性回归方程为 .
.
联考次数x(1≤x≤5,x∈N*) | 1 | 2 | 3 | 4 | 5 |
数学分数y(0<y≤150) | 117 | 127 | 125 | 134 | 142 |
(2)若在4月份开始进入冲刺复习前,该生的数学分数最好为116分,并以此作为初始分数,利用上述回归方程预测高考的数学成绩,并以预测高考成绩作为最终成绩,求该生4月份后复习提高率. (复习提高率=
 ×100%,分数取整数).
×100%,分数取整数).附:回归直线的斜率和截距的最小二乘估计公式分别为:
 ,
, ,其中
,其中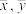 为样本平均值,
为样本平均值,线性回归方程为
 .
.
您最近半年使用:0次
2022-06-05更新
|
157次组卷
|
2卷引用:贵州省黔东南州2021-2022学年度高二下学期期末联考数学(文)试题
名校
解题方法
5 . 为调查某地区某种野生动物的数量,将其分成面积相近的 个地块,从这些地块中用简单随机抽样的方法抽取
个地块,从这些地块中用简单随机抽样的方法抽取 个作为样区,调查得到样本数据
个作为样区,调查得到样本数据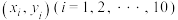 ,其中
,其中 和
和 分别表示第
分别表示第 个样区的植物覆盖面积(单位:公顷)和这种野生动物的数量,据分析野生动物的数量
个样区的植物覆盖面积(单位:公顷)和这种野生动物的数量,据分析野生动物的数量 与植物覆盖面积
与植物覆盖面积 线性相关并计算得
线性相关并计算得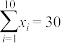 ,
,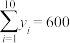 ,
,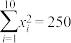 ,
,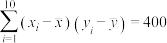 .
.
(1)求该地区植物覆盖面积和野生动物数量的回归直线方程;
(2)根据上述方程,预计该地区一块植物覆盖面积为 公顷的地块中这种野生动物的数量.
公顷的地块中这种野生动物的数量.
参考公式:回归直线方程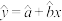 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: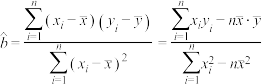 ,
, .
.
 个地块,从这些地块中用简单随机抽样的方法抽取
个地块,从这些地块中用简单随机抽样的方法抽取 个作为样区,调查得到样本数据
个作为样区,调查得到样本数据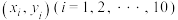 ,其中
,其中 和
和 分别表示第
分别表示第 个样区的植物覆盖面积(单位:公顷)和这种野生动物的数量,据分析野生动物的数量
个样区的植物覆盖面积(单位:公顷)和这种野生动物的数量,据分析野生动物的数量 与植物覆盖面积
与植物覆盖面积 线性相关并计算得
线性相关并计算得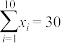 ,
,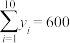 ,
,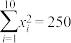 ,
,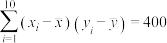 .
.(1)求该地区植物覆盖面积和野生动物数量的回归直线方程;
(2)根据上述方程,预计该地区一块植物覆盖面积为
 公顷的地块中这种野生动物的数量.
公顷的地块中这种野生动物的数量.参考公式:回归直线方程
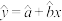 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: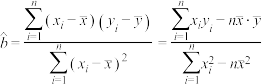 ,
, .
.
您最近半年使用:0次
2022-05-11更新
|
326次组卷
|
2卷引用:贵州省毕节市2022届高三下学期诊断性考试(三)数学(文)试题
名校
解题方法
6 . 我国在芯片领域的短板有光刻机和光刻胶,某风险投资公司准备投资芯片领域,若投资光刻机项目,据预期,每年的收益率为30%的概率为 ,收益率为
,收益率为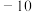 %的概率为
%的概率为 ;若投资光刻胶项目,据预期,每年的收益率为30%的概率为0.4,收益率为
;若投资光刻胶项目,据预期,每年的收益率为30%的概率为0.4,收益率为 %的概率为0.1,收益率为零的概率为0.5.
%的概率为0.1,收益率为零的概率为0.5.
(1)已知投资以上两个项目,获利的期望是一样的,请你从风险角度考虑为该公司选择一个较稳妥的项目;
(2)若该风险投资公司准备对以上你认为较稳妥的项目进行投资,4年累计投资数据如下表:
请根据上表提供的数据,用最小二乘法求出y关于 的线性回归方程
的线性回归方程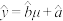 ,并预测到哪一年年末,该公司在芯片领域的投资收益预期能达到0.75亿元.
,并预测到哪一年年末,该公司在芯片领域的投资收益预期能达到0.75亿元.
附:收益=投入的资金×获利的期望;线性回归 中,
中,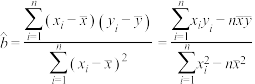 ,
, .
.
 ,收益率为
,收益率为 %的概率为
%的概率为 ;若投资光刻胶项目,据预期,每年的收益率为30%的概率为0.4,收益率为
;若投资光刻胶项目,据预期,每年的收益率为30%的概率为0.4,收益率为 %的概率为0.1,收益率为零的概率为0.5.
%的概率为0.1,收益率为零的概率为0.5.(1)已知投资以上两个项目,获利的期望是一样的,请你从风险角度考虑为该公司选择一个较稳妥的项目;
(2)若该风险投资公司准备对以上你认为较稳妥的项目进行投资,4年累计投资数据如下表:
| 年份x | 2018 | 2019 | 2020 | 2021 |
 | 1 | 2 | 3 | 4 |
| 累计投资金额y(单位:亿元) | 2 | 3 | 5 | 6 |
 的线性回归方程
的线性回归方程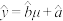 ,并预测到哪一年年末,该公司在芯片领域的投资收益预期能达到0.75亿元.
,并预测到哪一年年末,该公司在芯片领域的投资收益预期能达到0.75亿元.附:收益=投入的资金×获利的期望;线性回归
 中,
中,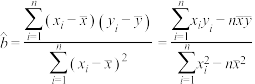 ,
, .
.
您最近半年使用:0次
2022-05-01更新
|
873次组卷
|
10卷引用:贵州省义龙新区2021届高三上学期末考试数学(理)试题
贵州省义龙新区2021届高三上学期末考试数学(理)试题(已下线)大题专练训练51:随机变量的分布列(相关关系)-2021届高三数学二轮复习陕西省商洛市2020-2021学年高三上学期期末理科数学试题吉林省白山市2020-2021学年高三上学期期末数学试题重庆市第三十七中学校2020-2021学年高二下学期5月月考数学试题广东省潮州市2022届高三下学期二模数学试题宁夏平罗中学2022届高三下学期第三次模拟数学(理)试题四川省眉山第一中学2022届高考适应性考试数学(理)试题福建省莆田市第一中学2021-2022学年高二下学期期末考试数学试题湖北省荆州市沙市中学2022-2023学年高三上学期第二次月考数学试题
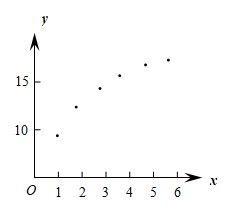
7 . 某企业为加强科研创新,加大研发资金的投入,新研发了一种产品.该产品的生产成本由直接生产成本(如原料、工人工资、机器设备折旧等)和间接生产成本(如物料消耗、管理人员工资、车间房屋折旧等)组成.该产品的间接生产成本y(万元)与该产品的生产数量x(千件)有关,经统计并对数据作初步处理,得到散点图及一些统计量的值.
表中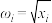 ,
,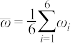 .
.
(1)根据散点图判断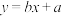 与
与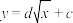 哪一个更适合作为间接生产成本y与该产品的生产数量x的回归方程类型;(给出判断即可,不必说明理由)
哪一个更适合作为间接生产成本y与该产品的生产数量x的回归方程类型;(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立y关于x的回归方程,并预测生产9千件产品时,间接生产成本是多少万元;
(3)为确保产品质量,该企业在生产过程中对生产的每件产品均进行五个环节的质量检测,若检测出不合格产品,则需在未进入下一环节前立即修复(修复后再进入下一环节),已知每个环节是相互独立的,且每个环节产品检测的合格率均为98%,各环节中不合格的一件产品所需的修复费用均为100元,求一件产品需修复的平均费用.
附:对于一组数据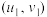 ,
,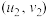 ,…,
,…,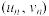 ,其回归直线
,其回归直线 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为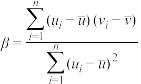 ,
,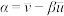 .
.

 | 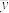 | 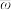 |  | 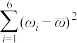 |  | 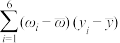 |
| 3.5 | 13.24 | 1.81 | 17.5 | 1.46 | 19.9 | 5.84 |
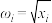 ,
, .
.(1)根据散点图判断
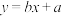 与
与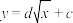 哪一个更适合作为间接生产成本y与该产品的生产数量x的回归方程类型;(给出判断即可,不必说明理由)
哪一个更适合作为间接生产成本y与该产品的生产数量x的回归方程类型;(给出判断即可,不必说明理由)(2)根据(1)的判断结果及表中数据,建立y关于x的回归方程,并预测生产9千件产品时,间接生产成本是多少万元;
(3)为确保产品质量,该企业在生产过程中对生产的每件产品均进行五个环节的质量检测,若检测出不合格产品,则需在未进入下一环节前立即修复(修复后再进入下一环节),已知每个环节是相互独立的,且每个环节产品检测的合格率均为98%,各环节中不合格的一件产品所需的修复费用均为100元,求一件产品需修复的平均费用.
附:对于一组数据
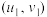 ,
,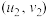 ,…,
,…,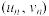 ,其回归直线
,其回归直线 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ,
,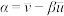 .
.
您最近半年使用:0次
8 . 某项科研活动共进行了5次试验,其数据如下表所示:
(1)从5次特征量y的试验数据中随机地抽取两个数据,求至少有一个大于600的概率;
(2)求特征量y关于x的线性回归方程 ,并预测当特征量x为570时,特征量y的值.
,并预测当特征量x为570时,特征量y的值.
(附:回归直线的斜率和截距的最小二乘法估计公式分别为 )
)
特征量 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
x | 555 | 559 | 551 | 563 | 552 |
y | 601 | 605 | 597 | 599 | 598 |
(2)求特征量y关于x的线性回归方程
 ,并预测当特征量x为570时,特征量y的值.
,并预测当特征量x为570时,特征量y的值.(附:回归直线的斜率和截距的最小二乘法估计公式分别为
 )
)
您最近半年使用:0次
2022-03-30更新
|
195次组卷
|
4卷引用:贵州省黔西南州金成实验学校2021-2022学年高二上学期期中数学(理)试题
名校
解题方法
9 . 小强5次考试的数学与物理成绩(满分100分)如下表,由散点图可知,小强的数学成绩x与物理成绩y之间线性相关.
(1)求y关于x的线性回归方程;
(2)利用(1)中的回归方程,小强第6次考试数学成绩是78分,请估计小强的物理分数.
附:回归直线的斜率和截距的最小二乘估计公式分别为: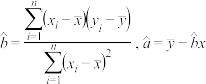
| 数学成绩x | 67 | 68 | 70 | 72 | 73 |
| 物理成绩y | 64 | 63 | 66 | 65 | 67 |
(2)利用(1)中的回归方程,小强第6次考试数学成绩是78分,请估计小强的物理分数.
附:回归直线的斜率和截距的最小二乘估计公式分别为:
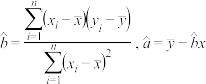
您最近半年使用:0次
2022-03-28更新
|
240次组卷
|
2卷引用:贵州师范大学附属中学2021-2022学年高二下学期开学考试数学(理)试题
名校
10 . 某超市在2017年五一正式开业,开业期间举行开业大酬宾活动,规定:一次购买总额在区间 内者可以参与一次抽奖,根据统计发现参与一次抽奖的顾客每次购买金额分布情况如下:
内者可以参与一次抽奖,根据统计发现参与一次抽奖的顾客每次购买金额分布情况如下:

(1)求参与一次抽奖的顾客购买金额的平均数与中位数(同一组中的数据用该组区间的中点值作代表,结果保留到整数);
(2)若根据超市的经营规律,购买金额 与平均利润
与平均利润 有以下四组数据:
有以下四组数据:
试根据所给数据,建立 关于
关于 的线性回归方程
的线性回归方程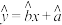 ,并根据1中计算的结果估计超市对每位顾客所得的利润
,并根据1中计算的结果估计超市对每位顾客所得的利润
参考公式: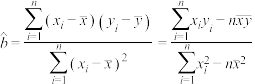 ,
,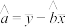
 内者可以参与一次抽奖,根据统计发现参与一次抽奖的顾客每次购买金额分布情况如下:
内者可以参与一次抽奖,根据统计发现参与一次抽奖的顾客每次购买金额分布情况如下:
(1)求参与一次抽奖的顾客购买金额的平均数与中位数(同一组中的数据用该组区间的中点值作代表,结果保留到整数);
(2)若根据超市的经营规律,购买金额
 与平均利润
与平均利润 有以下四组数据:
有以下四组数据:| 购买金额x(单位:元) | 100 | 200 | 300 | 400 |
| 利润:(单位:元) | 15 | 25 | 40 | 60 |
 关于
关于 的线性回归方程
的线性回归方程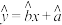 ,并根据1中计算的结果估计超市对每位顾客所得的利润
,并根据1中计算的结果估计超市对每位顾客所得的利润参考公式:
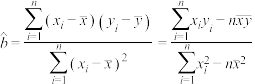 ,
,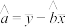
您最近半年使用:0次
2022-03-28更新
|
273次组卷
|
4卷引用:贵州省凯里市第一中学2018届高三下学期开学(第一次模拟)考试数学(文)试题
贵州省凯里市第一中学2018届高三下学期开学(第一次模拟)考试数学(文)试题新疆生产建设兵团第十师北屯高级中学2021-2022学年高二上学期月考(奥赛)数学试题(已下线)三轮冲刺卷04-【赢在高考·黄金20卷】备战2022年高考数学(理)模拟卷(全国卷专用)四川省眉山北外附属东坡外国语学校2022-2023学年高二下学期期中数学试题



