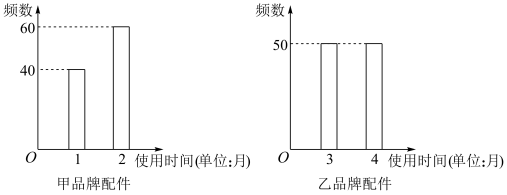
1 . 已知某工厂的一种机器有两个相同的易损配件,当两个配件都正常工作时(两个配件损坏与否互不影响),该机器才能正常运转.该工厂计划购买一批易损配件,现有甲、乙两个品牌的配件供选择,甲、乙两个品牌的配件可以搭配使用,甲品牌配件的价格为400元/个,乙品牌配件的价格为800元/个.现需决策如何购买易损配件,为此收集并整理了以往购买的甲、乙两个品牌配件各100个的使用时间的数据,得到如下柱状图.分别以甲、乙两种配件使用时间的频率作为概率.
(1)若从2个甲品牌配件和2个乙品牌配件中任选2个装入机器,求该机器正常运转时间不少于2个月的概率.
(2)现有两种购置方案:方案一,购置2个甲品牌配件;方案二,购置2个乙品牌配件.试从性价比(机器正常运转的时间的数学期望与成本的比值)的角度考虑,哪一种方案更实惠?
(1)若从2个甲品牌配件和2个乙品牌配件中任选2个装入机器,求该机器正常运转时间不少于2个月的概率.
(2)现有两种购置方案:方案一,购置2个甲品牌配件;方案二,购置2个乙品牌配件.试从性价比(机器正常运转的时间的数学期望与成本的比值)的角度考虑,哪一种方案更实惠?

您最近一年使用:0次
2022-05-26更新
|
516次组卷
|
4卷引用:河北省沧衡八校联盟2021-2022学年高二下学期期中数学试题
河北省沧衡八校联盟2021-2022学年高二下学期期中数学试题河南省许昌市2021-2022学年高二下学期期末数学理科试题(已下线)第07讲 离散型随机变量及其分布列和数字特征 (高频考点,精讲)(已下线)考点18 决策的选择问题 2024届高考数学考点总动员【练】
名校
解题方法
2 . 为深入贯彻党的十九大教育方针.中共中央办公厅、国务院办公厅印发《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》.郑州某中学数学建模小组随机抽查了我市2000名初二学生“双减”政策前后每天的运动时间,得到如下频数分布表:
表一:“双减”政策后
表二:“双减”政策前
(1)用一个数字特征描述“双减”政策给学生的运动时间带来的变化(同一时间段的数据用该组区间中点值做代表);
(2)为给参加运动的学生提供方便,学校在球场边安装直饮水设备.该设备需同时装配两个一级滤芯才能正常工作,且两个滤芯互不影响,一级滤芯有两个品牌A、B:A品牌售价5百元,使用寿命7个月或8个月(概率均为0.5);B品牌售价2百元,寿命3个月或4个月(概率均为0.5).现有两种购置方案,方案甲:购置2个品牌A;方案乙:购置1个品牌A和2个品牌B.试从性价比(设备正常运行时间与购置一级滤芯的成本之比)角度考虑,选择哪一种方案更实惠.
表一:“双减”政策后
| 时间(分钟) |  |  | 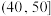 | 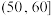 | 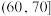 | 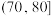 | 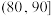 |
| 人数 | 10 | 60 | 210 | 520 | 730 | 345 | 125 |
| 时间(分钟) |  |  | 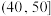 | 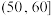 | 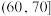 | 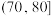 | 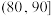 |
| 人数 | 40 | 245 | 560 | 610 | 403 | 130 | 12 |
(2)为给参加运动的学生提供方便,学校在球场边安装直饮水设备.该设备需同时装配两个一级滤芯才能正常工作,且两个滤芯互不影响,一级滤芯有两个品牌A、B:A品牌售价5百元,使用寿命7个月或8个月(概率均为0.5);B品牌售价2百元,寿命3个月或4个月(概率均为0.5).现有两种购置方案,方案甲:购置2个品牌A;方案乙:购置1个品牌A和2个品牌B.试从性价比(设备正常运行时间与购置一级滤芯的成本之比)角度考虑,选择哪一种方案更实惠.
您最近一年使用:0次
2022-01-14更新
|
747次组卷
|
4卷引用:河南省郑州市2021-2022学年高三上学期第一次质量预测理科数学试题
河南省郑州市2021-2022学年高三上学期第一次质量预测理科数学试题河南省鹤壁高中2021-2022学年高三下学期第七次模拟考试理科数学试题(已下线)二轮拔高卷04-【赢在高考·黄金20卷】备战2022年高考数学(理)模拟卷(全国卷专用)河北省唐山市、保定市四校(保定中恒高级中学有限公司等)2023届高三一模数学试题
名校
3 . 某公司全年圆满完成预定的生产任务,为答谢各位员工一年来的锐意进取和辛勤努力,公司决定在联欢晚会后,拟通过摸球兑奖的方式对500位员工进行奖励,规定:每位员工从一个装有4种面值的奖券的箱子中,一次随机摸出2张奖券,奖券上所标的面值之和就是该员工所获得的奖励额.
(1)若箱子中所装的4种面值的奖券中有1张面值为80元,其余3张均为40元,试比较员工获得80元奖励额与获得120元奖励额的概率的大小;
(2)公司对奖励总额的预算是6万元,预定箱子中所装的4种面值的奖券有两种方案:第一方案是2张面值20元和2张面值100元;第二方案是2张面值40元和2张面值80元.为了使员工得到的奖励总额尽可能地符合公司的预算且每位员工所获得的奖励额相对均衡,请问选择哪一种方案比较好?并说明理由.
(1)若箱子中所装的4种面值的奖券中有1张面值为80元,其余3张均为40元,试比较员工获得80元奖励额与获得120元奖励额的概率的大小;
(2)公司对奖励总额的预算是6万元,预定箱子中所装的4种面值的奖券有两种方案:第一方案是2张面值20元和2张面值100元;第二方案是2张面值40元和2张面值80元.为了使员工得到的奖励总额尽可能地符合公司的预算且每位员工所获得的奖励额相对均衡,请问选择哪一种方案比较好?并说明理由.
您最近一年使用:0次
2022-02-27更新
|
2317次组卷
|
10卷引用:技巧04 解答题解法与技巧(练)--第二篇 解题技巧篇-《2022年高考数学二轮复习讲练测(新高考·全国卷)》
(已下线)技巧04 解答题解法与技巧(练)--第二篇 解题技巧篇-《2022年高考数学二轮复习讲练测(新高考·全国卷)》重庆市万州第二高级中学2021-2022学年高二下学期期中数学试题重庆市万州纯阳中学校2021-2022学年高二下学期期中数学(A卷)试题(已下线)第06讲 离散型随机变量的均值与方差(核心考点讲与练)-2021-2022学年高二数学下学期考试满分全攻略(人教A版2019选修第二册+第三册)山东省大教育联盟学校2021-2022学年高三下学期收心考试(开学考试)数学试题福建省厦门集美中学2021-2022学年高二下学期期中考试数学试题(已下线)第07讲 离散型随机变量及其分布列和数字特征 (精讲)上海市延安中学2023届高三下学期开学考试数学试题(已下线)第七章 随机变量及其分布 全章总结 (精讲)(2)上海市曹杨第二中学2023届高三三模数学试题
名校
解题方法
4 . 潍坊市为切实保障疫情防控期间全市食品质量安全,采取食品安全监督抽检和第三方托管快检室相结合的方式,全面加强食品安全检验检测据了解,滩坊市市场监管部门组织开展对全市部分生产企业、农贸市场、大型商超、餐饮服务场所生产经营的小麦粉、大米、食用油、调味品、肉制品、乳制品等与人民群众日常生活关系密切且消费量大的食品进行监督抽检组织抽检400批次,抽检种类涵盖8大类31个品种全市各快检室快检60209批次,其中不合格53批次.某快检室在对乳制品进行抽检中,发现某品牌乳制品质量不合格,现随机抽取其5个批次的乳制品进行质量检测,已知其中有1个批次的乳制品质量不合格下面有两种检测方案:
方案甲:逐批次进行检测,直到确定质量不合格乳制品的批次;
方案乙:先任取3个批次的乳制品,将他们混合在一起检测.若结果不合格,则表明不合格批次就在这3个批次中,然后再逐个检测,直到能确定不合格乳制品的批次;若结果合格,则在另外2批次中,再任取1个批次检测.
(1)方案乙中,任取3个批次检测,求其中含有不合格乳制品批次的概率;
(2)求方案甲检测次数X的分布列;
(3)判断哪一种方案的效率更高,并说明理由.
方案甲:逐批次进行检测,直到确定质量不合格乳制品的批次;
方案乙:先任取3个批次的乳制品,将他们混合在一起检测.若结果不合格,则表明不合格批次就在这3个批次中,然后再逐个检测,直到能确定不合格乳制品的批次;若结果合格,则在另外2批次中,再任取1个批次检测.
(1)方案乙中,任取3个批次检测,求其中含有不合格乳制品批次的概率;
(2)求方案甲检测次数X的分布列;
(3)判断哪一种方案的效率更高,并说明理由.
您最近一年使用:0次
2020-12-20更新
|
1323次组卷
|
10卷引用:第47讲 概率分布-2022年新高考数学二轮专题突破精练
(已下线)第47讲 概率分布-2022年新高考数学二轮专题突破精练江苏省南京市宁海中学2022届高三下学期二模数学试题四川省宜宾市第四中学校2022-2023学年高三上学期12月月考数学(理科)试题(已下线)精做03 概率与统计-备战2021年高考数学大题精做(新高考专用)辽宁省阜新市第二十中学2023届高三下学期模拟考试数学试题山东省新高考质量测评联盟2020-2021学年高三上学期12月联合调研检测数学试题江苏省无锡市江阴市青阳中学2020-2021学年高三上学期1月阶段检测数学试题(已下线)必刷卷01-2021年高考数学考前信息必刷卷(江苏专用)(已下线)必刷卷03-2021年高考数学考前信息必刷卷(山东专用)(已下线)2021年秋季高三数学开学摸底考试卷01(江苏专用)
5 . 一工厂为了提高生产效率,对某型号生产设备进行了技术改造,为了对比改造前后的效果,采集了20台该种型号的设备技术改造前后连续正常运行的时间长度(单位:天)数据,整理如下表:
(1)根据所给数据,完成下面的 列联表,并判断能否有99%的把握认为技术改造前与技术改造后的连续正常运行时间有差异?
列联表,并判断能否有99%的把握认为技术改造前与技术改造后的连续正常运行时间有差异?
(2)若某台设备出现故障,则立即停工并申报维修,根据长期生产经验,每台设备停工 天的总损失额记为
天的总损失额记为 (单位:元)满足
(单位:元)满足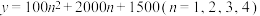 ,现有两种维修方案(一天完成维修)可供选择:
,现有两种维修方案(一天完成维修)可供选择:
方案一:加急维修单,维修人员会在设备出现故障的当天上门维修,维修费用为4000元;
方案二:常规维修单,维修人员会在设备出现故障当天或者之后3天中的任意一天上门维修,维修费用为1000元.
现统计该工厂最近100份常规维修单,获得每台设备在第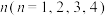 天得到维修的数据如下:
天得到维修的数据如下:
将频率视为概率,若某台设备出现故障,以该设备维修所需费用与停工总损失额的和的期望值为决策依据,应选择哪种维修方案?
 ,
,
设备编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
改造前 | 22 | 26 | 32 | 17 | 28 | 27 | 34 | 27 | 18 | 23 | 20 | 36 | 26 | 24 | 34 | 40 | 25 | 21 | 25 | 24 |
改造后 | 28 | 33 | 39 | 26 | 25 | 35 | 38 | 34 | 43 | 24 | 40 | 35 | 29 | 33 | 35 | 37 | 31 | 41 | 31 | 33 |
 列联表,并判断能否有99%的把握认为技术改造前与技术改造后的连续正常运行时间有差异?
列联表,并判断能否有99%的把握认为技术改造前与技术改造后的连续正常运行时间有差异?设备连续正常运行天数超过30天 | 设备连续正常运行天数未超过30天 | 合计 | |
改造前 | |||
改造后 | |||
合计 |
 天的总损失额记为
天的总损失额记为 (单位:元)满足
(单位:元)满足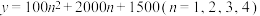 ,现有两种维修方案(一天完成维修)可供选择:
,现有两种维修方案(一天完成维修)可供选择:方案一:加急维修单,维修人员会在设备出现故障的当天上门维修,维修费用为4000元;
方案二:常规维修单,维修人员会在设备出现故障当天或者之后3天中的任意一天上门维修,维修费用为1000元.
现统计该工厂最近100份常规维修单,获得每台设备在第
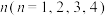 天得到维修的数据如下:
天得到维修的数据如下:
| 1 | 2 | 3 | 4 |
频数 | 10 | 30 | 40 | 20 |
 ,
,
| 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
您最近一年使用:0次
解题方法
6 . 某产品年末搞促销活动,由顾客投掷4枚相同的、质地均匀的硬币,若正面向上的硬币多于反面向上的硬币,则称该次投掷“顾客胜利”.顾客每买一件产品可以参加3次投掷活动,并且在投掷硬币之前,可以选择以下两种促销方案之一,获得一定数目的代金券.
方案一:顾客每投掷一次,若该次投掷“顾客胜利”,则顾客获得代金券 万元,否则该次投掷不获奖;
万元,否则该次投掷不获奖;
方案二:顾客获得的代金券金额和参加的3次投掷活动中“顾客胜利”次数关系如表:
(1)求顾客投掷一次硬币,该次投掷“顾客胜利”的概率;
(2)若某公司采购员小翁为公司采购很多件该产品,请从统计的角度来分析,小翁该采取哪种奖励方案?
方案一:顾客每投掷一次,若该次投掷“顾客胜利”,则顾客获得代金券
 万元,否则该次投掷不获奖;
万元,否则该次投掷不获奖;方案二:顾客获得的代金券金额和参加的3次投掷活动中“顾客胜利”次数关系如表:
| 获得代金券金额(万元) | 0 |  |  |  |
| “顾客胜利”次数 | 0 | 1 | 2 | 3 |
(2)若某公司采购员小翁为公司采购很多件该产品,请从统计的角度来分析,小翁该采取哪种奖励方案?
您最近一年使用:0次
2022-09-19更新
|
655次组卷
|
4卷引用:河南省驻马店市上蔡县衡水实验中学2022-2023学年高三上学期8月月考数学(理)试题
河南省驻马店市上蔡县衡水实验中学2022-2023学年高三上学期8月月考数学(理)试题(已下线)专题2二项分布运算(提升版)(已下线)专题49 两点分布、二项分布与超几何分布-3第六章 概率 能力提升 单元测试卷
名校
解题方法
7 . 某采购商从采购的一批水果中随机抽取100个,利用水果的等级分类标准得到的数据如下:
(1)若将频率视为概率,从这100个水果中有放回地随机抽取4个,求恰好有2个水果是礼品果的概率;(结果用分数表示)
(2)用样本估计总体,果园老板提出两种购销方案给采购商参考.
方案1:不分类卖出,售价为20元/kg;
方案2:分类卖出,分类后的水果售价如下.
从采购商的角度考虑,应该采用哪种方案?
(3)用分层抽样的方法从这100个水果中抽取10个,再从抽取的10个水果中随机抽取3个,X表示抽取的是精品果的数量,求X的分布列及数学期望.
等级 | 标准果 | 优质果 | 精品果 | 礼品果 |
个数 | 10 | 30 | 40 | 20 |
(2)用样本估计总体,果园老板提出两种购销方案给采购商参考.
方案1:不分类卖出,售价为20元/kg;
方案2:分类卖出,分类后的水果售价如下.
等级 | 标准果 | 优质果 | 精品果 | 礼品果 |
售价(元/ | 16 | 18 | 22 | 24 |
(3)用分层抽样的方法从这100个水果中抽取10个,再从抽取的10个水果中随机抽取3个,X表示抽取的是精品果的数量,求X的分布列及数学期望.
您最近一年使用:0次
2022-09-02更新
|
1385次组卷
|
39卷引用:人教A版(2019) 选修第三册 过关斩将 第七章 7.4.2 超几何分布
人教A版(2019) 选修第三册 过关斩将 第七章 7.4.2 超几何分布北京市师范大学第二附属中学2021-2022学年高二下学期期中考试数学试题河南省三门峡市2021-2022学年高二下学期期末质量检测理科数学试题山西省怀仁市大地中学高中部2021-2022学年高二下学期第三次月考数学试题云南省昆明市第三中学、滇池中学2021-2022学年高二下学期期中考试数学试题河北省唐山市滦南县2021-2022学年高二下学期期末数学试题宁夏银川市三沙源上游学校2023届高三上学期开学检测数学(理)试题2023版 湘教版(2019) 选修第二册 过关斩将 第3章 3.2.3离散型随机变量的数学期望(已下线)专题3超几何分布运算(提升版)(已下线)考向44事件的独立性与条件概率(重点)-1(已下线)2019年6月19日 《每日一题》理数(下学期期末复习)-离散型随机变量的均值与方差(已下线)专题10 概率与统计——2019年高考真题和模拟题理科数学分项汇编2020届辽宁省实验中学、大连八中、大连二十四中、鞍山一中、东北育才学校高三上学期期末数学(理)试题(已下线)专题06 离散型随机变量的期望与方差(第四篇)-备战2020年高考数学大题精做之解答题题型全覆盖宁夏银川市宁大附中2020届高三第五次模拟考试数学(理)试题(已下线)第二章随机变吸其分步单元测试(巅峰版) -突破满分数学之2019-2020学年高二数学(理)重难点突破(人教A版选修2-3)(已下线)综合测试卷(巅峰版) -突破满分数学之2019-2020学年高二数学(理)课时训练(人教A版选修2-3)(已下线)第三章统计案例单元测试(巅峰版) -突破满分数学之2019-2020学年高二数学(理)课时训练(人教A版选修2-3)陕西省西安中学2020-2021学年高三上学期第二次月考数学(理)试题广东省肇庆市封开县江口中学2018-2019学年高二下学期第二次期末模拟联考数学(理)试题(已下线)痛点16 概率与统计中的综合问题-2021年新高考数学一轮复习考点扫描(已下线)专题11.5 离散型随机变量的分布列、均值与方差 (精练)-2021年高考数学(理)一轮复习讲练测陕西省西安市长安区第一中学2020-2021学年高三上学期第三次月考数学(理)试题(已下线)专题9.2 离散型随机变量的均值与方差-备战2021年高考数学精选考点专项突破题集(新高考地区)(已下线)第08章:《期末综合试卷一》 (A卷基础篇)-2020-2021学年高二数学下学期同步单元AB卷(苏教版)山西省怀仁市第一中学2020-2021学年高二下学期期中数学(理)试题(已下线)解密21 统计与概率 (讲义)-【高频考点解密】2021年高考数学(理)二轮复习讲义+分层训练湖南省长沙市第一中学2020-2021学年高三上学期月考(二)数学试题人教B版(2019) 选修第二册 突围者 第四章 第二节课时4 随机变量的数字特征北师大版(2019) 选修第一册 突围者 第六章 第四节 课时2 超几何分布黑龙江省大庆市东风中学2021-2022学年高二下学期期中考试数学试题吉林地区普通高中友好学校联合体2021-2022学年高二下学期期末考试数学试题沪教版(2020) 一轮复习 堂堂清 第九单元 9.6 离散型随机变量及分布列(已下线)7.4.2 超几何分布 (精练)-【精讲精练】2022-2023学年高二数学下学期同步精讲精练(人教A版2019选择性必修第三册)【校级联考】江西省新八校2019届高三第二次联考理科数学试题1【校级联考】江西省新八校2019届高三第二次联考理科数学试题2山东省莱州市第一中学2019-2020学年高二下学期第二次检测数学试题(已下线)第06章:概率及分布列(A卷基础篇)-2020-2021学年高二数学下学期同步单元AB卷(苏教版)江西省兴国县第三中学2020-2021学年高二下学期第一次月考数学(理)(兴国班)试题
名校
8 . 某种大型医疗检查机器生产商,对一次性购买2台机器的客户,推出两种超过质保期后2年内的延保维修优惠方案.方案一:交纳延保金7000元,在延保的2年内可免费维修2次,超过2次每次收取维修费2000元;方案二:交纳延保差10000元,在延保的2年内可免费维修4次,超过4次每次收取维修费1000元.某医院准备一次性购买2台这种机器,现需决策在购买机器时应选择哪种延保方案,为此搜集并整理了50台这种机器超过质保期后延保2年内维修的次数,得下表:
将频率视为概率,记X表示这2台机器超过质保期后延保的2年内共需维修的次数.
(1)求X的分布列;
(2)以方案一与方案二所需费用(所需延保金友维修费用之和)的期望值为决策依据,医院选择哪种延保方案更合算?
| 维修次数 | 0 | 1 | 2 | 3 |
| 台数 | 5 | 10 | 20 | 15 |
(1)求X的分布列;
(2)以方案一与方案二所需费用(所需延保金友维修费用之和)的期望值为决策依据,医院选择哪种延保方案更合算?
您最近一年使用:0次
2022-04-15更新
|
363次组卷
|
21卷引用:人教A版(2019) 选修第三册 实战演练 第七章 易错疑难突破专练
人教A版(2019) 选修第三册 实战演练 第七章 易错疑难突破专练陕西省汉中市2022届高三下学期教学质量第二次检测考试理科数学试题【市级联考】安徽省合肥市2019届高三第二次教学质量检测数学(理)试题广东省惠州市2020届高三上学期第一次调研数学(理)试题广东省番禺区2020届高三摸底测试理科数学试题2020届湖南省怀化市麻阳一中高三下学期3月第七次月考数学(理)试题2020届全国100所名校高考模拟金典卷高三理科数学(八)试题(已下线)专题07 比较两类方法或者策略的分析问题(第四篇)-备战2020年高考数学大题精做之解答题题型全覆盖人教B版(2019) 选择性必修第二册 过关斩将 第四章 概率与统计 4.2 随机变量 4.2.4 随机变量的数字特征(已下线)专题11.5 离散型随机变量的分布列、均值与方差 (精讲)-2021年高考数学(理)一轮复习讲练测(已下线)7.3 离散型随机变量的数字特征(精练)-2020-2021学年高二数学一隅三反系列(人教A版2019选择性必修第三册)河北省正定中学2020-2021学年高二下学期第一次月考数学试题人教B版(2019) 选修第二册 过关检测 第四章 专题2 随机变量的分布列与数字特征(已下线)13.3 二项分布、超几何分布与数字特征甘肃省兰州市第五十七中学2022-2023学年高三下学期开学模拟考试数学(理科)试题【全国百强校】黑龙江省鹤岗市第一中学2018-2019学年高二下学期第二次月考数学(理)试题【全国百强校】重庆市南开中学2019届高三4月测试数学(理)试题【全国百强校】福建省厦门双十中学2020届高三上学期开学考试数学(理)试题2020届广西柳州高级中学高三下学期开学考试数学(理)试题广东省深圳市高级中学2018-2019学年高二下学期期末数学(理)试题2020届山东省潍坊市临朐县高三综合模拟考试数学试题(二)
名校
9 . 某班级体育课进行一次篮球定点投篮测试,规定每人最多投3次,每次投篮的结果相互独立.在A处每投进一球得3分,在B处每投进一球得2分,否则得0分.将学生得分逐次累加并用X表示,如果X的值不低于3分就判定为通过测试,立即停止投篮,否则应继续投篮,直到投完三次为止.现有两种投篮方案:方案1:先在A处投一球,以后都在B处投;方案2:都在B处投篮.已知甲同学在A处投篮的命中率为 ,在B处投篮的命中率为
,在B处投篮的命中率为 .
.
(1)若甲同学选择方案1,求他测试结束后所得总分X的分布列和数学期望E(X);
(2)你认为甲同学选择哪种方案通过测试的可能性更大?说明理由.
 ,在B处投篮的命中率为
,在B处投篮的命中率为 .
.(1)若甲同学选择方案1,求他测试结束后所得总分X的分布列和数学期望E(X);
(2)你认为甲同学选择哪种方案通过测试的可能性更大?说明理由.
您最近一年使用:0次
2022-08-15更新
|
887次组卷
|
13卷引用:山西省山西大学附属中学2021-2022学年高二下学期3月(总第二次)模块诊断数学试题
山西省山西大学附属中学2021-2022学年高二下学期3月(总第二次)模块诊断数学试题人教A版(2019) 选修第三册 过关斩将 第七章 7.1~7.3综合拔高练(已下线)第05讲 离散型随机变量及其分布列(核心考点讲与练)-2021-2022学年高二数学下学期考试满分全攻略(人教A版2019选修第二册+第三册)北京市广渠门中学2023届高三上学期10月月考数学试题(已下线)专题9.2 离散型随机变量的均值与方差-备战2021年高考数学精选考点专项突破题集(新高考地区)(已下线)大题专练训练48:随机变量的分布列(决策类)-2021届高三数学二轮复习山东省部分校2021-2022学年高三下学期数学开学摸底考试试题(已下线)第七章 随机变量及其分布 章节验收测评卷-【精讲精练】2022-2023学年高二数学下学期同步精讲精练(人教A版2019选择性必修第三册)(已下线)FHsx1225yl1702020届山东省济宁市第一中学高三下学期一轮质量检测数学试题(已下线)第 10 篇——概率统计-新高考山东专题汇编江西省新余市2021届高三上学期期末统考数学(理)试题湖北省鄂西北四校联考2021-2022学年高三上学期12月联考数学试题
名校
10 . 2021年新高考数学试卷中对每道多选题的得分规定:全部选对的得5分,部分选对的得2分,有选错的得0分.小明在做多选题的第11题、第12题时通常有两种策略:
策略 为避免选错只选出一个最有把握的选项.这种策略每个题耗时约3min.
为避免选错只选出一个最有把握的选项.这种策略每个题耗时约3min.
策略 选出自己认为正确的全部选项.这种策略每个题耗时约6min.
选出自己认为正确的全部选项.这种策略每个题耗时约6min.
某次数学考试临近,小明通过前期大量模拟训练得出了两种策略下第11题和第12题的作答情况如下:
第11题:如果采用策略 ,选对的概率为0.8,采用策略
,选对的概率为0.8,采用策略 ,部分选对的概率为0.5,全部选对的概率为0.4.
,部分选对的概率为0.5,全部选对的概率为0.4.
第12题:如果采用策略 ,选对的概率为0.7,采用策略
,选对的概率为0.7,采用策略 ,部分选对的概率为0.6,全部选对的概率为0.3.
,部分选对的概率为0.6,全部选对的概率为0.3.
如果这两题总用时超过10min,其他题目会因为时间紧张少得2分.假设小明作答两题的结果互不影响.
(1)若小明同学此次考试中决定第11题采用策略 、第12题采用策略
、第12题采用策略 ,设此次考试他第11题和第12题总得分为
,设此次考试他第11题和第12题总得分为 ,求
,求 的分布列.
的分布列.
(2)小明考前设计了以下两种方案:
方案1:第11题采用策略 ,第12题采用策略
,第12题采用策略 ;
;
方案2:第11题和第12题均采用策略 .
.
如果你是小明的指导老师,从整张试卷尽可能得分更高的角度出发,你赞成他的哪种方案?并说明理由.
策略
 为避免选错只选出一个最有把握的选项.这种策略每个题耗时约3min.
为避免选错只选出一个最有把握的选项.这种策略每个题耗时约3min.策略
 选出自己认为正确的全部选项.这种策略每个题耗时约6min.
选出自己认为正确的全部选项.这种策略每个题耗时约6min.某次数学考试临近,小明通过前期大量模拟训练得出了两种策略下第11题和第12题的作答情况如下:
第11题:如果采用策略
 ,选对的概率为0.8,采用策略
,选对的概率为0.8,采用策略 ,部分选对的概率为0.5,全部选对的概率为0.4.
,部分选对的概率为0.5,全部选对的概率为0.4.第12题:如果采用策略
 ,选对的概率为0.7,采用策略
,选对的概率为0.7,采用策略 ,部分选对的概率为0.6,全部选对的概率为0.3.
,部分选对的概率为0.6,全部选对的概率为0.3.如果这两题总用时超过10min,其他题目会因为时间紧张少得2分.假设小明作答两题的结果互不影响.
(1)若小明同学此次考试中决定第11题采用策略
 、第12题采用策略
、第12题采用策略 ,设此次考试他第11题和第12题总得分为
,设此次考试他第11题和第12题总得分为 ,求
,求 的分布列.
的分布列.(2)小明考前设计了以下两种方案:
方案1:第11题采用策略
 ,第12题采用策略
,第12题采用策略 ;
;方案2:第11题和第12题均采用策略
 .
.如果你是小明的指导老师,从整张试卷尽可能得分更高的角度出发,你赞成他的哪种方案?并说明理由.
您最近一年使用:0次
2022-08-12更新
|
709次组卷
|
9卷引用:山东省菏泽第一中学2021-2022学年高二下学期第三次阶段考试(月考)数学试题
山东省菏泽第一中学2021-2022学年高二下学期第三次阶段考试(月考)数学试题2023版 北师大版(2019) 选修第一册 突围者 第六章 全章综合检测2023版 北师大版(2019) 选修第一册 突围者 第六章 全章综合检测(已下线)第09讲 高考中的概率与统计 (精讲)-2山东省济南市2020-2021学年高二下学期期末数学试题福建师范大学附属中学2023届高三上学期第一次月考数学试题黑龙江省哈尔滨德强学校2022-2023学年高二下学期3月月考数学试题A湖北省鄂州市第二中学2022-2023学年高三下学期2月月考数学试题山东省新高考联合质量测评2022-2023学年高二下学期3月月考数学试题



 )
)

