名校
1 . 某学校号召学生参加“每天锻炼1小时”活动,为了解学生参加活动的情况,统计了全校所有学生在假期每周锻炼的时间,现随机抽取了60名同学在某一周参加锻炼的数据,整理如下 列联表:
列联表:
注:将一周参加锻炼时间不小于3小时的称为“经常锻炼”,其余的称为“不经常锻炼”.
(1)请完成上面 列联表,并依据小概率值
列联表,并依据小概率值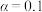 的独立性检验,能否认为性别因素与学生锻炼的经常性有关系;
的独立性检验,能否认为性别因素与学生锻炼的经常性有关系;
(2)将一周参加锻炼为0小时的称为“极度缺乏锻炼”.在抽取的60名同学中有5人“极度缺乏锻炼”.以样本频率估计概率.若在全校抽取20名同学,设“极度缺乏锻炼”的人数为X,求X的数学期望 和方差
和方差 ;
;
(3)将一周参加锻炼6小时以上的同学称为“运动爱好者”.在抽取的60名同学中有10名“运动爱好者”,其中有7名男生,3名女生.为进一步了解他们的生活习惯,在10名“运动爱好者”中,随机抽取3人进行访谈,设抽取的3人中男生人数为Y,求Y的分布列和数学期望.
附: ,
,
 列联表:
列联表:性别 | 不经常锻炼 | 经常锻炼 | 合计 |
男生 | 7 | ||
女生 | 16 | 30 | |
合计 | 21 |
(1)请完成上面
 列联表,并依据小概率值
列联表,并依据小概率值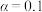 的独立性检验,能否认为性别因素与学生锻炼的经常性有关系;
的独立性检验,能否认为性别因素与学生锻炼的经常性有关系;(2)将一周参加锻炼为0小时的称为“极度缺乏锻炼”.在抽取的60名同学中有5人“极度缺乏锻炼”.以样本频率估计概率.若在全校抽取20名同学,设“极度缺乏锻炼”的人数为X,求X的数学期望
 和方差
和方差 ;
;(3)将一周参加锻炼6小时以上的同学称为“运动爱好者”.在抽取的60名同学中有10名“运动爱好者”,其中有7名男生,3名女生.为进一步了解他们的生活习惯,在10名“运动爱好者”中,随机抽取3人进行访谈,设抽取的3人中男生人数为Y,求Y的分布列和数学期望.
附:
 ,
,
| 0.1 | 0.05 | 0.01 |
| 2.706 | 3.841 | 6.635 |
您最近一年使用:0次
2024-05-09更新
|
1767次组卷
|
12卷引用:专题07 回归方程与独立性检验--高二期末考点大串讲(苏教版2019选择性必修第二册)
(已下线)专题07 回归方程与独立性检验--高二期末考点大串讲(苏教版2019选择性必修第二册)江苏省盐城中学、南京二十九中联考2023-2024学年高二下学期4月期中数学试题江苏省苏州实验中学2023-2024学年高二下学期5月月考数学试题江苏省淮安市洪泽中学,金湖中学,清河中学,清浦中学等学校2023-2024学年高二下学期5月月考数学试题(已下线)第1套 期末全真模拟卷(高二期末中等卷)湖北省部分重点中学2023-2024学年高二下学期五月联考数学试卷广东省江门市鹤山市第一中学2023-2024学年高二下学期第二阶段考试(5月)数学试题山东省滕州市第五中学2023-2024学年高二下学期第四次单元检测(第二次月考)数学试题福建省福州市闽侯县第一中学2023-2024学年高二下学期第二次月考(5月)数学试题辽宁省七校协作体2023-2024学年高二下学期6月月考数学试题江西省南昌市第十中学2023-2024学年高二下学期第二次月考数学试题黑龙江省哈尔滨市双城区兆麟中学2023-2024学年高二下学期第二次月考(6月)数学试题
名校
2 . 2024年1月4日,教育部在京召开全国“双减”工作视频调度会,会议要求进一步提高双减政治站位,将“双减”工作作为重中之重,坚定不移推进,成为受老师和家长关注的重要话题.某学校为了解家长对双减工作的满意程度进行问卷调查(评价结果仅有“满意”、“不满意”),从所有参与评价的对象中随机抽取120人进行调查,部分数据如表所示(单位:人):
(1)请将 列联表补充完整,试根据小概率值
列联表补充完整,试根据小概率值 的独立性检验,能否认为“对双减工作满意程度的评价与性别有关”?
的独立性检验,能否认为“对双减工作满意程度的评价与性别有关”?
(2)若将频率视为概率,从所有给出“满意”的家长中随机抽取3人,用随机变量 表示被抽到的男性家长的人数,求
表示被抽到的男性家长的人数,求 的分布列;
的分布列;
(3)在抽出的120人中,从给出“满意”的家长中利用分层抽样的方法抽取10人,从给出“不满意”的对象中抽取 人.现从这
人.现从这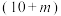 人中,随机抽出2人,用随机变量
人中,随机抽出2人,用随机变量 表示被抽到的给出“满意”的女性家长的人数.若随机变量
表示被抽到的给出“满意”的女性家长的人数.若随机变量 的数学期望不小于1,求
的数学期望不小于1,求 的最大值.
的最大值.
参考公式: ,其中
,其中 .
.
参考数据:
满意 | 不满意 | 合计 | |
男性 | 10 | 50 | |
女性 | 60 | ||
合计 | 120 |
 列联表补充完整,试根据小概率值
列联表补充完整,试根据小概率值 的独立性检验,能否认为“对双减工作满意程度的评价与性别有关”?
的独立性检验,能否认为“对双减工作满意程度的评价与性别有关”?(2)若将频率视为概率,从所有给出“满意”的家长中随机抽取3人,用随机变量
 表示被抽到的男性家长的人数,求
表示被抽到的男性家长的人数,求 的分布列;
的分布列;(3)在抽出的120人中,从给出“满意”的家长中利用分层抽样的方法抽取10人,从给出“不满意”的对象中抽取
 人.现从这
人.现从这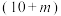 人中,随机抽出2人,用随机变量
人中,随机抽出2人,用随机变量 表示被抽到的给出“满意”的女性家长的人数.若随机变量
表示被抽到的给出“满意”的女性家长的人数.若随机变量 的数学期望不小于1,求
的数学期望不小于1,求 的最大值.
的最大值.参考公式:
 ,其中
,其中 .
.参考数据:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
您最近一年使用:0次
2024-05-08更新
|
737次组卷
|
5卷引用:专题07 回归方程与独立性检验--高二期末考点大串讲(苏教版2019选择性必修第二册)
(已下线)专题07 回归方程与独立性检验--高二期末考点大串讲(苏教版2019选择性必修第二册)吉林省长春市第八中学2023-2024学年高二下学期第一次月考数学试题(已下线)第八章:成对数据的统计分析章末综合检测卷(新题型)-2023-2024学年高二数学题型分类归纳讲与练(人教A版2019选择性必修第三册)河南省百师联盟联考2023-2024学年高二下学期6月联考数学试题吉林省长春市文理高中2023-2024学年高二下学期5月月考数学试题
名校
解题方法
3 . 已知某校篮球队共有9名队员,其中5名主力队员,4名替补队员.在某次训练中,该校篮球队教练从中随机地挑选3名队员进行投篮训练,每名队员至多投篮5次,一旦连续命中2次或者投完5次,都停止投篮.
(1)记选出的3名队员中主力队员的人数为随机变量 ,求
,求 的概率分布和数学期望;
的概率分布和数学期望;
(2)已知队员甲被选中参加投篮训练,假定队员甲每次投篮命中率均为 ,记队员甲投篮次数为随机变量
,记队员甲投篮次数为随机变量 ,求
,求 的概率分布和数学期望.
的概率分布和数学期望.
(1)记选出的3名队员中主力队员的人数为随机变量
 ,求
,求 的概率分布和数学期望;
的概率分布和数学期望;(2)已知队员甲被选中参加投篮训练,假定队员甲每次投篮命中率均为
 ,记队员甲投篮次数为随机变量
,记队员甲投篮次数为随机变量 ,求
,求 的概率分布和数学期望.
的概率分布和数学期望.
您最近一年使用:0次
4 . 为推动党史学习教育工作扎实开展,营造“学党史、悟思想、办实事、开新局”的浓厚氛围,某校党委决定在教师党员中开展“学党史”知识竞赛.甲老师从装有6个不同问题的纸盒中依次不放回抽取4个问题作答.已知这6个问题中,甲能正确回答其中的4个问题,且甲老师对每个问题回答正确与否都是相互独立、互不影响的.
(1)求甲老师答对2个问题的概率;
(2)若测试过程中答对1个问题得2分,答错得0分,设随机变量 表示甲的得分,求
表示甲的得分,求 .
.
(1)求甲老师答对2个问题的概率;
(2)若测试过程中答对1个问题得2分,答错得0分,设随机变量
 表示甲的得分,求
表示甲的得分,求 .
.
您最近一年使用:0次
2024-05-08更新
|
838次组卷
|
5卷引用:专题05 离散型随机变量的分布列常考点(8类题型)-备战2023-2024学年高二数学下学期期末真题分类汇编(江苏专用)
(已下线)专题05 离散型随机变量的分布列常考点(8类题型)-备战2023-2024学年高二数学下学期期末真题分类汇编(江苏专用)江苏省盐城市三校2023-2024学年高二下学期4月期中联考数学试题(已下线)专题04 随机变量的均值与方差综合--高二期末考点大串讲(人教B版2019选择性必修第二册)(已下线)作业03 概率(1)-【暑假分层作业】(苏教版2019选择性必修第二册)(已下线)第三章 随机变量及其分布列 专题三 重要的概率分布模型 微点1 重要的概率分布模型(一)【基础版】
名校
5 . 某省2023年开始将全面实施新高考方案.在6门选择性考试科目中,物理、历史这两门科目采用原始分计分:思想政治、地理、化学、生物这4门科目采用等级转换赋分,将每科考生的原始分从高到低划分为A、B,C,D,E共5个等级,各等级人数所占比例分别为15%、35%、35%、13%和2%,并按给定的公式进行转换赋分.该省部分学校联合组织了一次高二年级统一考试,并对思想政治、地理、化学、生物这4门科目的原始分进行了等级转换赋分.
(1)其中一所学校某班生物学科获得A等级的共有10名学生,其原始分及转换赋分如表:
现从这10名学生中随机抽取3人,设这3人中生物的赋分不低于95分的人数为X,求X的分布列和数学期望:
(2)假设此次高二学生生物学科原始分Y近似服从正态分布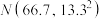 .现随机抽取了100名高二学生的此次生物学科的原始分,后经调查发现其中有一名学生舞弊,剔除掉这名学生成绩后,记ξ为其他被抽到的原始分不低于80分的学生人数,预测当
.现随机抽取了100名高二学生的此次生物学科的原始分,后经调查发现其中有一名学生舞弊,剔除掉这名学生成绩后,记ξ为其他被抽到的原始分不低于80分的学生人数,预测当 取得最大值时k的值.
取得最大值时k的值.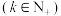
附,若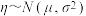 ,则
,则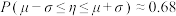 ,
,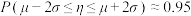 .
.
(1)其中一所学校某班生物学科获得A等级的共有10名学生,其原始分及转换赋分如表:
| 原始分 | 97 | 95 | 91 | 90 | 89 | 87 | 85 | 84 | 84 | 83 |
| 赋分 | 99 | 97 | 95 | 95 | 94 | 92 | 91 | 90 | 90 | 90 |
(2)假设此次高二学生生物学科原始分Y近似服从正态分布
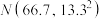 .现随机抽取了100名高二学生的此次生物学科的原始分,后经调查发现其中有一名学生舞弊,剔除掉这名学生成绩后,记ξ为其他被抽到的原始分不低于80分的学生人数,预测当
.现随机抽取了100名高二学生的此次生物学科的原始分,后经调查发现其中有一名学生舞弊,剔除掉这名学生成绩后,记ξ为其他被抽到的原始分不低于80分的学生人数,预测当 取得最大值时k的值.
取得最大值时k的值.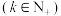
附,若
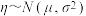 ,则
,则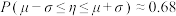 ,
,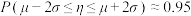 .
.
您最近一年使用:0次
2024-04-30更新
|
999次组卷
|
9卷引用:专题06 离散型随机变量分布列及正态分布--高二期末考点大串讲(苏教版2019选择性必修第二册)
(已下线)专题06 离散型随机变量分布列及正态分布--高二期末考点大串讲(苏教版2019选择性必修第二册)(已下线)7.5 正态分布(6大题型)精讲-2023-2024学年高二数学题型分类归纳讲与练(人教A版2019选择性必修第三册)(已下线)高二期末模拟卷01(已下线)专题03 第七章 随机变量及其分布列--高二期末考点大串讲(人教A版2019)(已下线)专题06 离散型随机变量与正态分布--高二期末考点大串讲(苏教版2019选择性必修第二册)(已下线)第五章 概率统计创新问题 专题三 概率统计中的函数思想 微点3 概率统计中的函数思想综合训练【基础版】江西省景德镇市一中2023-2024学年高二下学期4月期中考试数学试题山东省济宁市第一中学2023-2024学年高二下学期质量检测(三)(6月)数学试题广东省深圳市人大附中深圳学校2023-2024学年高二下学期期中考试数学试卷
名校
6 . 刷脸时代来了,人们为“刷脸支付”给生活带来的便捷感到高兴,但“刷脸支付”的安全性也引起了人们的担忧.某调查机构为了解人们对“刷脸支付”的接受程度,通过安全感问卷进行调查(问卷得分在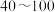 分之间),并从参与者中随机抽取
分之间),并从参与者中随机抽取 人.根据调查结果绘制出如图所示的频率分布直方图.
人.根据调查结果绘制出如图所示的频率分布直方图.
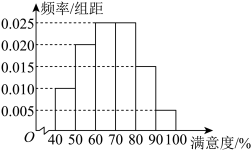
(1)据此估计这 人满意度的平均数
人满意度的平均数 同一组中的数据用该组区间的中点值作代表
同一组中的数据用该组区间的中点值作代表 ;
;
(2)某大型超市引入“刷脸支付”后,在推广“刷脸支付”期间,推出两种付款方案:方案一:不采用“刷脸支付”,无任何优惠,但可参加超市的抽奖返现金活动.活动方案为:从装有 个形状、大小完全相同的小球
个形状、大小完全相同的小球 其中红球
其中红球 个,黑球
个,黑球 个
个 的抽奖盒中,一次性摸出
的抽奖盒中,一次性摸出 个球,若摸到
个球,若摸到 个红球,返消费金额的
个红球,返消费金额的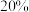 ;若摸到
;若摸到 个红球,返消费金额的
个红球,返消费金额的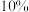 ,除此之外不返现金.
,除此之外不返现金.
方案二:采用“刷脸支付”,此时对购物的顾客随机优惠,但不参加超市的抽奖返现金活动,根据统计结果得知,使用“刷脸支付”时有 的概率享受
的概率享受 折优惠,有
折优惠,有 的概率享受
的概率享受 折优惠,有
折优惠,有 的概率享受
的概率享受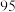 折优惠.现小张在该超市购买了总价为
折优惠.现小张在该超市购买了总价为 元的商品.
元的商品.
①求小张选择方案一付款时实际付款额 的分布列与数学期望;
的分布列与数学期望;
②试从期望角度,比较小张选择方案一与方案二付款,哪个方案更划算?(注:结果精确到 )
)
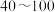 分之间),并从参与者中随机抽取
分之间),并从参与者中随机抽取 人.根据调查结果绘制出如图所示的频率分布直方图.
人.根据调查结果绘制出如图所示的频率分布直方图.
(1)据此估计这
 人满意度的平均数
人满意度的平均数 同一组中的数据用该组区间的中点值作代表
同一组中的数据用该组区间的中点值作代表 ;
;(2)某大型超市引入“刷脸支付”后,在推广“刷脸支付”期间,推出两种付款方案:方案一:不采用“刷脸支付”,无任何优惠,但可参加超市的抽奖返现金活动.活动方案为:从装有
 个形状、大小完全相同的小球
个形状、大小完全相同的小球 其中红球
其中红球 个,黑球
个,黑球 个
个 的抽奖盒中,一次性摸出
的抽奖盒中,一次性摸出 个球,若摸到
个球,若摸到 个红球,返消费金额的
个红球,返消费金额的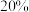 ;若摸到
;若摸到 个红球,返消费金额的
个红球,返消费金额的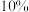 ,除此之外不返现金.
,除此之外不返现金.方案二:采用“刷脸支付”,此时对购物的顾客随机优惠,但不参加超市的抽奖返现金活动,根据统计结果得知,使用“刷脸支付”时有
 的概率享受
的概率享受 折优惠,有
折优惠,有 的概率享受
的概率享受 折优惠,有
折优惠,有 的概率享受
的概率享受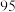 折优惠.现小张在该超市购买了总价为
折优惠.现小张在该超市购买了总价为 元的商品.
元的商品.①求小张选择方案一付款时实际付款额
 的分布列与数学期望;
的分布列与数学期望;②试从期望角度,比较小张选择方案一与方案二付款,哪个方案更划算?(注:结果精确到
 )
)
您最近一年使用:0次
2024-04-30更新
|
1878次组卷
|
7卷引用:专题05 离散型随机变量的分布列常考点(8类题型)-备战2023-2024学年高二数学下学期期末真题分类汇编(江苏专用)
(已下线)专题05 离散型随机变量的分布列常考点(8类题型)-备战2023-2024学年高二数学下学期期末真题分类汇编(江苏专用)(已下线)9.1 随机抽样与统计图标(高考真题素材之十年高考)宁夏回族自治区石嘴山市平罗中学2024届高三下学期第三次模拟考试数学(理)试题上海市金山中学2023-2024学年高二下学期5月月考数学试卷湖南省长沙市长郡中学2024届高三下学期模拟(三)数学试题辽宁省沈阳市东北育才学校2024届高三考前最后一模数学试题广东省茂名市高州中学2025届高三上学期8月月考数学试题
名校
解题方法
7 . 2024年“与辉同行”直播间开播,董宇辉领衔7位主播从“心”出发,其中男性5人,女性3人,现需排班晚8:00黄金档,随机抽取两人,则男生人数的期望为( )
A. | B. | C.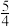 | D.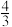 |
您最近一年使用:0次
2024-03-31更新
|
1436次组卷
|
8卷引用:专题05 离散型随机变量的分布列常考点(8类题型)-备战2023-2024学年高二数学下学期期末真题分类汇编(江苏专用)
(已下线)专题05 离散型随机变量的分布列常考点(8类题型)-备战2023-2024学年高二数学下学期期末真题分类汇编(江苏专用)(已下线)专题06 离散型随机变量分布列及正态分布--高二期末考点大串讲(苏教版2019选择性必修第二册)(已下线)7.4 二项分布与超几何分布(8大题型)精讲-2023-2024学年高二数学题型分类归纳讲与练(人教A版2019选择性必修第三册)(已下线)专题04 随机变量的均值与方差综合--高二期末考点大串讲(人教B版2019选择性必修第二册)吉林省长春市东北师范大学附属中学2023-2024学年高二下学期3月月考数学试题安徽省六安市六安第一中学2024届高考模拟预测数学试题(四)江西省宜春市宜丰中学创新部2023-2024学年高一下学期6月月考数学试题四川省自贡市第一中学校2023-2024学年高二下学期6月月考数学试题
名校
解题方法
8 . 为深入学习贯彻党的二十大精神,推动全市党员干部群众用好“学习强国”学习平台,激发干事创业热情.某单位组织“学习强国”知识竞赛,竞赛共有 道题目,随机抽取
道题目,随机抽取 道让参赛者回答.已知小明只能答对其中的
道让参赛者回答.已知小明只能答对其中的 道,试求:
道,试求:
(1)抽到他能答对题目数 的分布列;
的分布列;
(2)求 的期望和方差
的期望和方差
 道题目,随机抽取
道题目,随机抽取 道让参赛者回答.已知小明只能答对其中的
道让参赛者回答.已知小明只能答对其中的 道,试求:
道,试求:(1)抽到他能答对题目数
 的分布列;
的分布列;(2)求
 的期望和方差
的期望和方差
您最近一年使用:0次
2024-03-19更新
|
2681次组卷
|
10卷引用:第8章 概率 章末题型归纳总结-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)
(已下线)第8章 概率 章末题型归纳总结-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)(已下线)8.2 离散型随机变量及其分布列(3)江苏高二专题08概率与统计(第二部分)江苏省无锡市运河实验学校2023-2024学年高二下学期期中考试数学试卷(已下线)第七章:随机变量及其分布章末重点题型复习(7题型)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)(已下线)专题07概率初步(续)全章复习攻略--高二期末考点大串讲(沪教版2020选修)(已下线)第三章 随机变量及其分布列 专题三 重要的概率分布模型 微点1 重要的概率分布模型(一)【基础版】上海市位育中学2023-2024学年高二下学期3月月考数学试卷河北省沧州市吴桥县吴桥中学2023-2024学年高二下学期3月月考数学试题浙江省学军中学紫金港校区2023-2024学年高二下学期期中数学试题
名校
解题方法
9 . “英才计划”最早开始于2013年,由中国科协、教育部共同组织实施,到2023年已经培养了6000多名具有创新潜质的优秀中学生,为选拔培养对象,某高校在暑假期间从中学里挑选优秀学生参加数学、物理、化学学科夏令营活动.
(1)若数学组的7名学员中恰有3人来自 中学,从这7名学员中选取3人,
中学,从这7名学员中选取3人, 表示选取的人中来自
表示选取的人中来自 中学的人数,求
中学的人数,求 的分布列和数学期望;
的分布列和数学期望;
(2)在夏令营开幕式的晚会上,物理组举行了一次学科知识竞答活动,规则如下:两人一组,每一轮竞答中,每人分别答两题,若小组答对题数不小于3,则取得本轮胜利.已知甲乙两位同学组成一组,甲、乙答对每道题的概率分别为 ,
, .假设甲、乙两人每次答题相互独立,且互不影响.当
.假设甲、乙两人每次答题相互独立,且互不影响.当 时,求甲、乙两位同学在每轮答题中取胜的概率的最大值.
时,求甲、乙两位同学在每轮答题中取胜的概率的最大值.
(1)若数学组的7名学员中恰有3人来自
 中学,从这7名学员中选取3人,
中学,从这7名学员中选取3人, 表示选取的人中来自
表示选取的人中来自 中学的人数,求
中学的人数,求 的分布列和数学期望;
的分布列和数学期望;(2)在夏令营开幕式的晚会上,物理组举行了一次学科知识竞答活动,规则如下:两人一组,每一轮竞答中,每人分别答两题,若小组答对题数不小于3,则取得本轮胜利.已知甲乙两位同学组成一组,甲、乙答对每道题的概率分别为
 ,
, .假设甲、乙两人每次答题相互独立,且互不影响.当
.假设甲、乙两人每次答题相互独立,且互不影响.当 时,求甲、乙两位同学在每轮答题中取胜的概率的最大值.
时,求甲、乙两位同学在每轮答题中取胜的概率的最大值.
您最近一年使用:0次
2024-02-27更新
|
4451次组卷
|
16卷引用:第8章 概率 章末题型归纳总结-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)
(已下线)第8章 概率 章末题型归纳总结-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)(已下线)7.4.2超几何分布(分层练习,4大题型)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)(已下线)专题09 计数原理与随机变量及分布列(讲义)(已下线)二项分布与超几何分布、正态分布-一轮复习考点专练浙江省杭州第二中学2023-2024学年高三下学期开学考试数学试卷安徽省江南十校2024届高三联考信息卷数学模拟预测卷(一)(已下线)第3套-期初重组模拟卷广东省深圳市东北师范大学附属中学深圳学校2024届高三下学期3月校内模拟测试数学试题四川省成都市教育科学研究院附属中学2023-2024学年高三下学期4月综合测试数学(理科)试题2024届河北省邢台市部分高中二模数学试题甘肃省白银市靖远县第一中学2024届高三下学期模拟预测数学试题河北省衡水中学2023-2024学年高三下学期期中自我提升测试数学试题辽宁省沈阳市五校协作体2023-2024学年高二下学期期末考试数学试题江西省宜春市丰城市第九中学2024-2025学年高二日新班上学期第一次段考数学试卷吉林省长春市文理高中2025届高三上学期校二模考试数学试题山东省泰安市新泰市紫光实验中学2024-2025学年高三上学期开学检测数学试题
名校
10 . 某袋中装有大小相同、质地均匀的6个球,其中4个黑球和2个白球.从袋中随机取出2个球,记取出白球的个数为X.
(1)写出X的分布列,并求出 和
和 的值;
的值;
(2)若取出一个白球得一分,取出一个黑球得两分,最后得分为Z,求出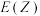 和
和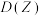 的值.
的值.
(1)写出X的分布列,并求出
 和
和 的值;
的值;(2)若取出一个白球得一分,取出一个黑球得两分,最后得分为Z,求出
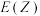 和
和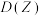 的值.
的值.
您最近一年使用:0次
2024-02-03更新
|
949次组卷
|
8卷引用:8.2 离散型随机变量及其分布列(1)
(已下线)8.2 离散型随机变量及其分布列(1)(已下线)第07讲 7.4.2超几何分布-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第三册)(已下线)专题04 随机变量的均值与方差综合--高二期末考点大串讲(人教B版2019选择性必修第二册)(已下线)专题03 随机变量及其分布列-2(已下线)离散型随机变量及其分布列、数字特征-一轮复习考点专练湖南省长沙市第一中学2023-2024学年高二上学期期末考试数学试题河北省衡水市武强中学2023-2024学年高二下学期期中考试数学试题(已下线)7.4.2 超几何分布——课堂例题