1 . 无人驾驶被视为推动社会进步和改善生活质量的重要工具,但其安全性和对劳动就业的影响也受到人们的质疑.为了解某大学的学生对无人驾驶的态度,随机调查了该校96名大学生,调查结果如下表所示:
用样本的频率分布估计该校每名学生对无人驾驶态度的概率分布,且学生的态度相互独立.为衡量学生对无人驾驶的支持程度,每名支持者得5分,每名中立者得3分,每名反对者得1分.
(1)从该校任选2名学生,求他们的得分不相同的概率.
(2)从该校任选3名学生,求他们的得分之和为7的概率.
(3)从该校任选n名学生,其中得分为5的学生人数为X,若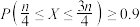 ,利用下面所给的两个结论,求正整数n的最小值.
,利用下面所给的两个结论,求正整数n的最小值.
结论一:若随机变量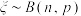 ,则随机变量
,则随机变量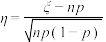 近似服从正态分布
近似服从正态分布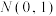 ;
;
结论二:若随机变量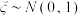 ,则
,则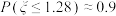 ,
,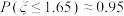 .
.
对无人驾驶的态度 | 支持 | 中立 | 反对 |
频数 | 48 | 32 | 16 |
(1)从该校任选2名学生,求他们的得分不相同的概率.
(2)从该校任选3名学生,求他们的得分之和为7的概率.
(3)从该校任选n名学生,其中得分为5的学生人数为X,若
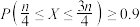 ,利用下面所给的两个结论,求正整数n的最小值.
,利用下面所给的两个结论,求正整数n的最小值.结论一:若随机变量
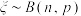 ,则随机变量
,则随机变量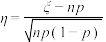 近似服从正态分布
近似服从正态分布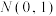 ;
;结论二:若随机变量
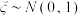 ,则
,则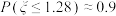 ,
,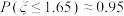 .
.
您最近一年使用:0次
2 . 贵妃杏是河南省灵宝市黄河沿岸地区的一种水果,其果实个大似鹅蛋,外表呈橙黄色,阳面有晕.贵妃杏口感甜美,肉质实心鲜嫩多汁,营养丰富,是河南省的知名特产之一.已知该地区某种植园成熟的贵妃杏(按个计算)的质量 (单位:克)服从正态分布
(单位:克)服从正态分布 ,且
,且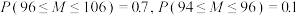 .从该种植园成熟的贵妃杏中选取了10个,它们的质量(单位:克)为
.从该种植园成熟的贵妃杏中选取了10个,它们的质量(单位:克)为 ,这10个贵妃杏的平均质量恰等于
,这10个贵妃杏的平均质量恰等于 克.
克.
(1)求 .
.
(2)求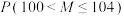 .
.
(3)甲和乙都从该种植园成熟的贵妃杏中随机选取1个,若选取的贵妃杏的质量大于100克且不大于104克,则赠送1个贵妃杏;若选取的贵妃杏的质量大于104克,则赠送2个贵妃杏.记甲和乙获赠贵妃杏的总个数为 ,求
,求 的分布列与数学期望.
的分布列与数学期望.
 (单位:克)服从正态分布
(单位:克)服从正态分布 ,且
,且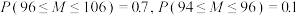 .从该种植园成熟的贵妃杏中选取了10个,它们的质量(单位:克)为
.从该种植园成熟的贵妃杏中选取了10个,它们的质量(单位:克)为 ,这10个贵妃杏的平均质量恰等于
,这10个贵妃杏的平均质量恰等于 克.
克.(1)求
 .
.(2)求
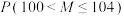 .
.(3)甲和乙都从该种植园成熟的贵妃杏中随机选取1个,若选取的贵妃杏的质量大于100克且不大于104克,则赠送1个贵妃杏;若选取的贵妃杏的质量大于104克,则赠送2个贵妃杏.记甲和乙获赠贵妃杏的总个数为
 ,求
,求 的分布列与数学期望.
的分布列与数学期望.
您最近一年使用:0次
昨日更新
|
241次组卷
|
5卷引用:河北省邢台市质检联盟2024-2025学年高三上学期第一次月考(10月)数学试题
名校
3 . 已知连续型随机变量 与离散型随机变量
与离散型随机变量 满足
满足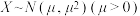 ,
,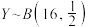 ,若
,若 与
与 的方差相同且
的方差相同且 ,则
,则 ( ).
( ).
 与离散型随机变量
与离散型随机变量 满足
满足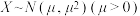 ,
,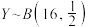 ,若
,若 与
与 的方差相同且
的方差相同且 ,则
,则 ( ).
( ).A. | B. | C. | D. |
您最近一年使用:0次
2024高三·全国·专题练习
4 . 按照国际乒联的规定,标准的乒乓球在直径符合的条件下,重量为2.7克,其重量的误差在区间[-0.081,0.081]内就认为是合格产品,在正常情况下样本的重量误差x服从正态分布.现从某厂生产的一批产品中随机抽取10件样本,其重量如下:
2.72 2.68 2.7 2.75 2.66 2.7 2.6 2.69 2.7 2.8
(1)计算上述10件产品的误差的平均数及标准差s;
(2)①利用(1)中求的平均数,标准差s,估计这批产品的合格率能否达到96%;
②如果产品的误差服从正态分布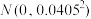 ,那么从这批产品中随机抽取10件产品,则有不合格产品的概率为多少?(附:若随机变量x服从正态分布
,那么从这批产品中随机抽取10件产品,则有不合格产品的概率为多少?(附:若随机变量x服从正态分布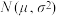 ,则
,则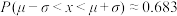 ,
,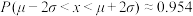 ,
,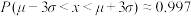 ,
,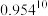 用0.624,
用0.624, 用0.9704分别代替计算)
用0.9704分别代替计算)
2.72 2.68 2.7 2.75 2.66 2.7 2.6 2.69 2.7 2.8
(1)计算上述10件产品的误差的平均数及标准差s;
(2)①利用(1)中求的平均数,标准差s,估计这批产品的合格率能否达到96%;
②如果产品的误差服从正态分布
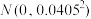 ,那么从这批产品中随机抽取10件产品,则有不合格产品的概率为多少?(附:若随机变量x服从正态分布
,那么从这批产品中随机抽取10件产品,则有不合格产品的概率为多少?(附:若随机变量x服从正态分布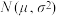 ,则
,则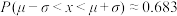 ,
,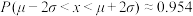 ,
,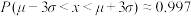 ,
,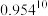 用0.624,
用0.624, 用0.9704分别代替计算)
用0.9704分别代替计算)
您最近一年使用:0次
名校
5 . 芯片时常制造在半导体晶元表面上.某企业使用新技术对某款芯片制造工艺进行改进.部分芯片由智能检测系统进行筛选,其中部分次品芯片会被淘汰,筛选后的芯片及未经筛选的芯片进入流水线由工人进行抽样检验.记A表示事件“某芯片通过智能检测系统筛选”,B表示事件“某芯片经人工抽检后合格”.改进生产工艺后,这款芯片的某项质量指标 服从正态分布
服从正态分布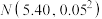 ,现从中随机抽取M个,这M个芯片中恰有m个的质量指标
,现从中随机抽取M个,这M个芯片中恰有m个的质量指标 位于区间
位于区间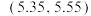 ,则下列说法正确的是( )(参考数据:
,则下列说法正确的是( )(参考数据: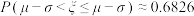 ,
,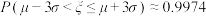 )
)
 服从正态分布
服从正态分布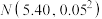 ,现从中随机抽取M个,这M个芯片中恰有m个的质量指标
,现从中随机抽取M个,这M个芯片中恰有m个的质量指标 位于区间
位于区间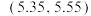 ,则下列说法正确的是( )(参考数据:
,则下列说法正确的是( )(参考数据: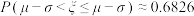 ,
,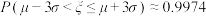 )
)A.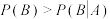 |
B.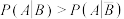 |
C.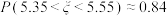 |
D. 取得最大值时,M的估计值为54 取得最大值时,M的估计值为54 |
您最近一年使用:0次
名校
6 . 某校机器人社团为了解市民对历年"数博会"科技成果的关注情况,在市内随机抽取了1000名市民进行问卷调查,问卷调查的成绩 近似服从正态分布
近似服从正态分布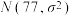 ,且
,且 .
.
(1)估计抽取市民中问卷成绩在80分以上的市民人数;
(2)若本次问卷调查得分超过80分,则认为该市民对“数博会”的关注度较高,现从市内随机抽取3名市民,记对“数博会”关注度较高的市民人数为随机变量 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
 近似服从正态分布
近似服从正态分布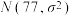 ,且
,且 .
.(1)估计抽取市民中问卷成绩在80分以上的市民人数;
(2)若本次问卷调查得分超过80分,则认为该市民对“数博会”的关注度较高,现从市内随机抽取3名市民,记对“数博会”关注度较高的市民人数为随机变量
 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
您最近一年使用:0次
解题方法
7 . 若随机变量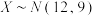 ,则下列选项错误的是( )
,则下列选项错误的是( )
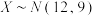 ,则下列选项错误的是( )
,则下列选项错误的是( )A.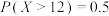 | B.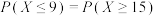 |
C. | D. |
您最近一年使用:0次
名校
8 . 某汽车公司最新研发了一款新能源汽车,并在出厂前对100辆汽车进行了单次最大续航里程(理论上是指新能源汽车所装载的燃料或电池所能够提供给车行驶的最远里程)的测试.现对测试数据进行整理,得到如下的频率分布直方图: (同一组中的数据用该组区间的中点值代表);
(同一组中的数据用该组区间的中点值代表);
(2)由频率分布直方图计算得样本标准差s的近似值为49.75.根据大量的汽车测试数据,可以认为这款汽车的单次最大续航里程X近似地服从正态分布 ,其中μ近似为样本平均数
,其中μ近似为样本平均数 ,σ近似为样本标准差S.
,σ近似为样本标准差S.
(ⅰ)利用该正态分布,求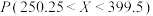 ;
;
(ⅱ)假设某企业从该汽车公司购买了20辆该款新能源汽车,记Z表示这20辆新能源汽车中单次最大续航里程位于区间(250.25,399.5)的车辆数,求E(Z);
参考数据:若随机变量ξ服从正态分布 ,则
,则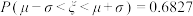 ,
,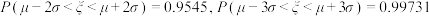 .
.
(3)某汽车销售公司为推广此款新能源汽车,现面向意向客户推出“玩游戏,送大奖”活动,客户可根据抛掷硬币的结果,操控微型遥控车在x轴上从原点O出发向右运动,已知硬币出现正、反面的概率都 ,客户每掷一次硬币,遥控车向右移动一次,若掷出正面,则遥控车向移动一个单位,若掷出反面,则遥控车向右移动两个单位,直到遥控车移到点(59,0)(胜利大本营)或点(60,0)(失败大本营)时,游戏结束,若遥控车最终停在“胜利大本营”,则可获得购车优惠券.设遥控车移到点
,客户每掷一次硬币,遥控车向右移动一次,若掷出正面,则遥控车向移动一个单位,若掷出反面,则遥控车向右移动两个单位,直到遥控车移到点(59,0)(胜利大本营)或点(60,0)(失败大本营)时,游戏结束,若遥控车最终停在“胜利大本营”,则可获得购车优惠券.设遥控车移到点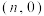 的概率为
的概率为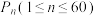 ,试证明数列
,试证明数列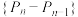 是等比数列
是等比数列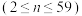 ,求出数列
,求出数列 的通项公式,并比较
的通项公式,并比较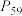 和
和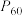 的大小.
的大小.
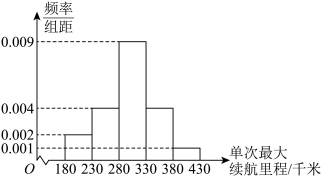
 (同一组中的数据用该组区间的中点值代表);
(同一组中的数据用该组区间的中点值代表);(2)由频率分布直方图计算得样本标准差s的近似值为49.75.根据大量的汽车测试数据,可以认为这款汽车的单次最大续航里程X近似地服从正态分布
 ,其中μ近似为样本平均数
,其中μ近似为样本平均数 ,σ近似为样本标准差S.
,σ近似为样本标准差S.(ⅰ)利用该正态分布,求
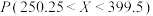 ;
;(ⅱ)假设某企业从该汽车公司购买了20辆该款新能源汽车,记Z表示这20辆新能源汽车中单次最大续航里程位于区间(250.25,399.5)的车辆数,求E(Z);
参考数据:若随机变量ξ服从正态分布
 ,则
,则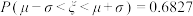 ,
,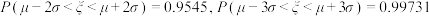 .
.(3)某汽车销售公司为推广此款新能源汽车,现面向意向客户推出“玩游戏,送大奖”活动,客户可根据抛掷硬币的结果,操控微型遥控车在x轴上从原点O出发向右运动,已知硬币出现正、反面的概率都
 ,客户每掷一次硬币,遥控车向右移动一次,若掷出正面,则遥控车向移动一个单位,若掷出反面,则遥控车向右移动两个单位,直到遥控车移到点(59,0)(胜利大本营)或点(60,0)(失败大本营)时,游戏结束,若遥控车最终停在“胜利大本营”,则可获得购车优惠券.设遥控车移到点
,客户每掷一次硬币,遥控车向右移动一次,若掷出正面,则遥控车向移动一个单位,若掷出反面,则遥控车向右移动两个单位,直到遥控车移到点(59,0)(胜利大本营)或点(60,0)(失败大本营)时,游戏结束,若遥控车最终停在“胜利大本营”,则可获得购车优惠券.设遥控车移到点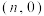 的概率为
的概率为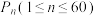 ,试证明数列
,试证明数列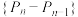 是等比数列
是等比数列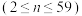 ,求出数列
,求出数列 的通项公式,并比较
的通项公式,并比较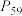 和
和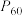 的大小.
的大小.
您最近一年使用:0次
2024-10-14更新
|
519次组卷
|
4卷引用:山西省长治市2024-2025学年高三上学期9月质量监测数学试题
山西省长治市2024-2025学年高三上学期9月质量监测数学试题(已下线)第五章 概率统计创新问题 专题二 概率统计与数列交汇 微点1 概率统计与数列交汇(一)【培优版】辽宁省三校2025届高三上学期10月联合教学质量检测数学试卷重庆市乌江新高考协作体2025届高三上学期高考质量调研(二)(10月)数学试题
解题方法
9 . 若随机变量 ,从
,从 的取值中随机抽取
的取值中随机抽取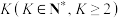 个数据,记这
个数据,记这 个数据的平均值为
个数据的平均值为 ,则随机变量
,则随机变量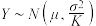 .随机变量
.随机变量 服从正态分布
服从正态分布 ,则
,则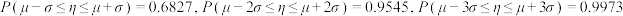 .某珠宝店出售的珍珠的直径均服从期望为15毫米,标准差为2毫米的正态分布.程女士在该珠宝店随机地挑选了16颗圆润华美的珍珠,将它串成一条璀璨夺目的项链.设这16颗珍珠的直径平均值为
.某珠宝店出售的珍珠的直径均服从期望为15毫米,标准差为2毫米的正态分布.程女士在该珠宝店随机地挑选了16颗圆润华美的珍珠,将它串成一条璀璨夺目的项链.设这16颗珍珠的直径平均值为 ,则( )
,则( )
 ,从
,从 的取值中随机抽取
的取值中随机抽取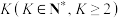 个数据,记这
个数据,记这 个数据的平均值为
个数据的平均值为 ,则随机变量
,则随机变量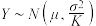 .随机变量
.随机变量 服从正态分布
服从正态分布 ,则
,则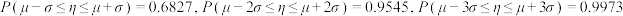 .某珠宝店出售的珍珠的直径均服从期望为15毫米,标准差为2毫米的正态分布.程女士在该珠宝店随机地挑选了16颗圆润华美的珍珠,将它串成一条璀璨夺目的项链.设这16颗珍珠的直径平均值为
.某珠宝店出售的珍珠的直径均服从期望为15毫米,标准差为2毫米的正态分布.程女士在该珠宝店随机地挑选了16颗圆润华美的珍珠,将它串成一条璀璨夺目的项链.设这16颗珍珠的直径平均值为 ,则( )
,则( )A.随机变量 的标准差为 的标准差为 | B.随机变量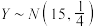 |
C.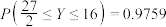 | D.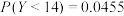 |
您最近一年使用:0次
10 . 在某市举行的一次期末质量检测中,经抽样分析,该市某学校的数学成绩X近似服从正态分布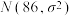 ,且
,且 .该校有1000人参加此次考试,则( )
.该校有1000人参加此次考试,则( )
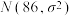 ,且
,且 .该校有1000人参加此次考试,则( )
.该校有1000人参加此次考试,则( )A. |
B. |
| C.估计成绩不低于90分的有200人 |
| D.估计成绩不低于86分的有300人 |
您最近一年使用:0次



