名校
1 . 《山东省高考改革试点方案》规定: 年高考总成绩由语文、数学、外语三门统考科目和思想政治、历史、地理、物理、化学、生物六门选考科目组成,将每门选考科目的考生原始成绩从高到低划分为
年高考总成绩由语文、数学、外语三门统考科目和思想政治、历史、地理、物理、化学、生物六门选考科目组成,将每门选考科目的考生原始成绩从高到低划分为 、
、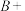 、
、 、
、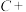 、
、 、
、 、
、 、
、 共8个等级,参照正态分布原则,确定各等级人数所占比例分别为
共8个等级,参照正态分布原则,确定各等级人数所占比例分别为 、
、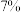 、
、 、
、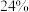 、
、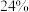 、
、 、
、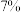 、
、 ,选择科目成绩计入考生总成绩时,将
,选择科目成绩计入考生总成绩时,将 至
至 等级内的考生原始成绩
等级内的考生原始成绩 ,依照
,依照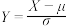 (
( 、
、 分别为正态分布的均值和标准差)分别转换到
分别为正态分布的均值和标准差)分别转换到 、
、 、
、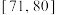 、
、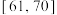 、
、 、
、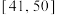 、
、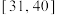 、
、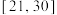 八个分数区间,得到考生的等级成绩.如果山东省
八个分数区间,得到考生的等级成绩.如果山东省 年某次学业水平模拟考试物理科目的原始成绩
年某次学业水平模拟考试物理科目的原始成绩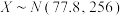 ,
,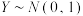 .
.
(1)若规定等级 、
、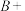 、
、 、
、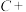 、
、 、
、 为合格,
为合格, 、
、 为不合格,需要补考,估计这次学业水平模拟考试物理合格线的最低原始分是多少;
为不合格,需要补考,估计这次学业水平模拟考试物理合格线的最低原始分是多少;
(2)现随机抽取了该省 名参加此次物理学科学业水平测试的原始分,若这些学生的原始分相互独立,记
名参加此次物理学科学业水平测试的原始分,若这些学生的原始分相互独立,记 为被抽到的原始分不低于
为被抽到的原始分不低于 分的学生人数,求
分的学生人数,求 的数学期望和方差.
的数学期望和方差.
附:当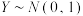 时,
时,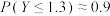 ,
,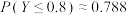 .
.
 年高考总成绩由语文、数学、外语三门统考科目和思想政治、历史、地理、物理、化学、生物六门选考科目组成,将每门选考科目的考生原始成绩从高到低划分为
年高考总成绩由语文、数学、外语三门统考科目和思想政治、历史、地理、物理、化学、生物六门选考科目组成,将每门选考科目的考生原始成绩从高到低划分为 、
、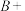 、
、 、
、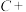 、
、 、
、 、
、 、
、 共8个等级,参照正态分布原则,确定各等级人数所占比例分别为
共8个等级,参照正态分布原则,确定各等级人数所占比例分别为 、
、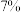 、
、 、
、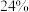 、
、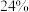 、
、 、
、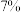 、
、 ,选择科目成绩计入考生总成绩时,将
,选择科目成绩计入考生总成绩时,将 至
至 等级内的考生原始成绩
等级内的考生原始成绩 ,依照
,依照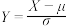 (
( 、
、 分别为正态分布的均值和标准差)分别转换到
分别为正态分布的均值和标准差)分别转换到 、
、 、
、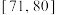 、
、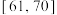 、
、 、
、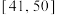 、
、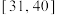 、
、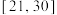 八个分数区间,得到考生的等级成绩.如果山东省
八个分数区间,得到考生的等级成绩.如果山东省 年某次学业水平模拟考试物理科目的原始成绩
年某次学业水平模拟考试物理科目的原始成绩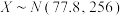 ,
,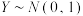 .
.(1)若规定等级
 、
、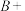 、
、 、
、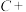 、
、 、
、 为合格,
为合格, 、
、 为不合格,需要补考,估计这次学业水平模拟考试物理合格线的最低原始分是多少;
为不合格,需要补考,估计这次学业水平模拟考试物理合格线的最低原始分是多少;(2)现随机抽取了该省
 名参加此次物理学科学业水平测试的原始分,若这些学生的原始分相互独立,记
名参加此次物理学科学业水平测试的原始分,若这些学生的原始分相互独立,记 为被抽到的原始分不低于
为被抽到的原始分不低于 分的学生人数,求
分的学生人数,求 的数学期望和方差.
的数学期望和方差.附:当
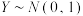 时,
时,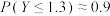 ,
,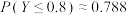 .
.
您最近半年使用:0次
2022-05-31更新
|
1268次组卷
|
7卷引用:2022届河南省开封市部分学校高三下学期押题理科数学试题
2022届河南省开封市部分学校高三下学期押题理科数学试题河南省兰考县第一高级中学2022届高三考前押题卷理科数学试题(已下线)专题50 正态分布-2(已下线)考向42 四大分布:两点分布、二项分布、超几何分布与正态分布(十大经典题型)-3(已下线)第08讲 两点分布、二项分布、超几何分布与正态分布(十一大题型)(讲义)-3(已下线)专题21 概率与统计的综合运用(13大核心考点)(讲义)(已下线)8.3 正态分布(七大题型)-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)
名校
2 . 已知某高校共有10000名学生,其图书馆阅览室共有994个座位,假设学生是否去自习是相互独立的,且每个学生在每天的晚自习时间去阅览室自习的概率均为0.1.
(1)将每天的晚自习时间去阅览室自习的学生人数记为 ,求
,求 的期望和方差;
的期望和方差;
(2)18世纪30年代,数学家棣莫弗发现,当 比较大时,二项分布可视为正态分布.此外,如果随机变量
比较大时,二项分布可视为正态分布.此外,如果随机变量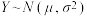 ,令
,令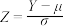 ,则
,则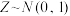 .当
.当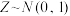 时,对于任意实数
时,对于任意实数 ,记
,记 .已知下表为标准正态分布表(节选),该表用于查询标准正态分布
.已知下表为标准正态分布表(节选),该表用于查询标准正态分布 对应的概率值.例如当
对应的概率值.例如当 时,由于
时,由于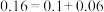 ,则先在表的最左列找到数字0.1(位于第三行),然后在表的最上行找到数字0.06(位于第八列),则表中位于第三行第八列的数字0.5636便是
,则先在表的最左列找到数字0.1(位于第三行),然后在表的最上行找到数字0.06(位于第八列),则表中位于第三行第八列的数字0.5636便是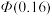 的值.
的值.
①求在晚自习时间阅览室座位不够用的概率;
②若要使在晚自习时间阅览室座位够用的概率高于0.7,则至少需要添加多少个座位?
(1)将每天的晚自习时间去阅览室自习的学生人数记为
 ,求
,求 的期望和方差;
的期望和方差;(2)18世纪30年代,数学家棣莫弗发现,当
 比较大时,二项分布可视为正态分布.此外,如果随机变量
比较大时,二项分布可视为正态分布.此外,如果随机变量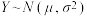 ,令
,令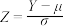 ,则
,则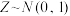 .当
.当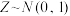 时,对于任意实数
时,对于任意实数 ,记
,记 .已知下表为标准正态分布表(节选),该表用于查询标准正态分布
.已知下表为标准正态分布表(节选),该表用于查询标准正态分布 对应的概率值.例如当
对应的概率值.例如当 时,由于
时,由于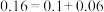 ,则先在表的最左列找到数字0.1(位于第三行),然后在表的最上行找到数字0.06(位于第八列),则表中位于第三行第八列的数字0.5636便是
,则先在表的最左列找到数字0.1(位于第三行),然后在表的最上行找到数字0.06(位于第八列),则表中位于第三行第八列的数字0.5636便是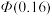 的值.
的值. | 0.00 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 |
| 0.0 | 0.5000 | 0.5040 | 0.5080 | 0.5120 | 0.5160 | 0.5199 | 0.5239 | 0.5279 | 0.5319 | 0.5359 |
| 0.1 | 0.5398 | 0.5438 | 0.5478 | 0.5517 | 0.5557 | 0.5596 | 0.5636 | 0.5675 | 0.5714 | 0.5753 |
| 0.2 | 0.5793 | 0.5832 | 0.5871 | 0.5910 | 0.5948 | 0.5987 | 0.6026 | 0.6064 | 0.6103 | 0.6141 |
| 0.3 | 0.6179 | 0.6217 | 0.6255 | 0.6293 | 0.6331 | 0.6368 | 0.6404 | 0.6443 | 0.6480 | 0.6517 |
| 0.4 | 0.6554 | 0.6591 | 0.6628 | 0.6664 | 0.6700 | 0.6736 | 0.6772 | 0.6808, | 0.6844 | 0.6879 |
| 0.5 | 0.6915 | 0.6950 | 0.6985 | 0.7019 | 0.7054 | 0.7088 | 0.7123 | 0.7157' | 0.7190 | 0.7224 |
②若要使在晚自习时间阅览室座位够用的概率高于0.7,则至少需要添加多少个座位?
您最近半年使用:0次
2021-06-05更新
|
2029次组卷
|
11卷引用:河南省郑州市第十一中学2020-2021学年高二下学期期末数学试题
河南省郑州市第十一中学2020-2021学年高二下学期期末数学试题广东省深圳市2021届高三下学期二模数学试题福建省福建师范大学附属中学2021届高三启明级校模拟考试数学试题甘肃省民乐县第一中学2021届高三押题卷(三)数学(理)试题(已下线)专题50 正态分布-2(已下线)考向42 四大分布:两点分布、二项分布、超几何分布与正态分布(十大经典题型)-3(已下线)专题10 概率与统计的综合运用(精讲精练)-1上海师范大学附属中学2022-2023学年高二下学期期末数学试题(已下线)第08讲 两点分布、二项分布、超几何分布与正态分布(十一大题型)(讲义)-3(已下线)专题21 概率与统计的综合运用(13大题型)(练习)(已下线)8.3 正态分布(七大题型)-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)
名校
解题方法
3 . 2020年某地在全国志愿服务信息系统注册登记志愿者8万多人.2019年7月份以来,共完成1931个志愿服务项目,8900多名志愿者开展志愿服务活动累计超过150万小时.为了了解此地志愿者对志愿服务的认知和参与度,随机调查了500名志愿者每月的志愿服务时长(单位:小时),并绘制如图所示的频率分布直方图.

(1)求这500名志愿者每月志愿服务时长的样本平均数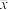 和样本方差
和样本方差 (同一组中的数据用该组区间的中间值代表);
(同一组中的数据用该组区间的中间值代表);
(2)由直方图可以认为,目前该地志愿者每月服务时长 服从正态分布
服从正态分布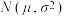 ,其中
,其中 近似为样本平均数
近似为样本平均数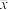 ,
, 近似为样本方差
近似为样本方差 .一般正态分布的概率都可以转化为标准正态分布的概率进行计算:若
.一般正态分布的概率都可以转化为标准正态分布的概率进行计算:若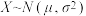 ,令
,令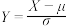 ,则
,则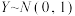 ,且
,且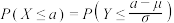 .
.
(ⅰ)利用直方图得到的正态分布,求 ;
;
(ⅱ)从该地随机抽取20名志愿者,记 表示这20名志愿者中每月志愿服务时长超过10小时的人数,求
表示这20名志愿者中每月志愿服务时长超过10小时的人数,求 (结果精确到0.001)以及
(结果精确到0.001)以及 的数学期望.
的数学期望.
参考数据: ,
,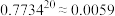 .若
.若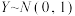 ,则
,则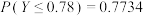 .
.

(1)求这500名志愿者每月志愿服务时长的样本平均数
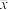 和样本方差
和样本方差 (同一组中的数据用该组区间的中间值代表);
(同一组中的数据用该组区间的中间值代表);(2)由直方图可以认为,目前该地志愿者每月服务时长
 服从正态分布
服从正态分布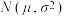 ,其中
,其中 近似为样本平均数
近似为样本平均数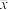 ,
, 近似为样本方差
近似为样本方差 .一般正态分布的概率都可以转化为标准正态分布的概率进行计算:若
.一般正态分布的概率都可以转化为标准正态分布的概率进行计算:若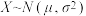 ,令
,令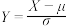 ,则
,则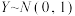 ,且
,且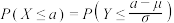 .
.(ⅰ)利用直方图得到的正态分布,求
 ;
;(ⅱ)从该地随机抽取20名志愿者,记
 表示这20名志愿者中每月志愿服务时长超过10小时的人数,求
表示这20名志愿者中每月志愿服务时长超过10小时的人数,求 (结果精确到0.001)以及
(结果精确到0.001)以及 的数学期望.
的数学期望.参考数据:
 ,
,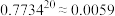 .若
.若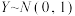 ,则
,则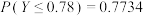 .
.
您最近半年使用:0次
2021-03-23更新
|
3222次组卷
|
15卷引用:河南省济源(平顶山许昌市)2021届高三第二次质量检测理科数学试题
河南省济源(平顶山许昌市)2021届高三第二次质量检测理科数学试题(已下线)黄金卷20-【赢在高考·黄金20卷】备战2021年高考数学全真模拟卷(山东高考专用)(已下线)专题23 概率与统计相结合问题(讲)-2021年高三数学二轮复习讲练测(新高考版)(已下线)专题27 概率与统计相结合问题(讲)-2021年高三数学二轮复习讲练测(文理通用)(已下线)专题7.6第七章《随机变量及其分布列》综合测试卷(B卷提升篇)-2020-2021学年高二下学期数学选择性必修第三册同步单元AB卷(新教材人教A版,浙江专用)辽宁省部分重点高中2020-2021学年高二下学期期中考试数学试题安徽省六安市舒城中学2021届高三下学期仿真模拟(三)理科数学试题(已下线)解密21 统计与概率(分层训练)-【高频考点解密】2021年高考数学(理)二轮复习讲义+分层训练(已下线)押第18题 概率与统计-备战2021年高考数学(理)临考题号押题(全国卷2)(已下线)7.5正态分布B卷(已下线)专题50 正态分布-2山西省2024届高三上学期优生联考数学试题黑龙江省齐齐哈尔市龙西北高中名校联盟2023-2024学年高三上学期期末联合考试数学试题(已下线)第08讲 7.5 正态分布(1)(已下线)8.3 正态分布(七大题型)-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)
名校
4 . 某校高三年级有1000人,某次考试不同成绩段的人数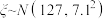 ,且所有得分都是整数.
,且所有得分都是整数.
(1)求全班平均成绩;
(2)计算得分超过141的人数;(精确到整数)
(3)甲同学每次考试进入年级前100名的概率是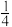 ,若本学期有4次考试,
,若本学期有4次考试, 表示进入前100名的次数,写出
表示进入前100名的次数,写出 的分布列,并求期望与方差.
的分布列,并求期望与方差.
参考数据: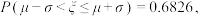
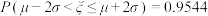 .
.
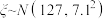 ,且所有得分都是整数.
,且所有得分都是整数.(1)求全班平均成绩;
(2)计算得分超过141的人数;(精确到整数)
(3)甲同学每次考试进入年级前100名的概率是
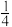 ,若本学期有4次考试,
,若本学期有4次考试, 表示进入前100名的次数,写出
表示进入前100名的次数,写出 的分布列,并求期望与方差.
的分布列,并求期望与方差.参考数据:
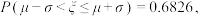
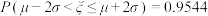 .
.
您最近半年使用:0次
2018-02-23更新
|
1109次组卷
|
4卷引用:河南省周口市项城市第三高级中学2022-2023学年高二下学期第三次考试数学试卷(B)
河南省周口市项城市第三高级中学2022-2023学年高二下学期第三次考试数学试卷(B)衡水金卷2018年普通高等学校招生全国统一考试 分科综合卷 理科数学(二)模拟试题(已下线)2018年高考数学备考中等生百日捷进提升系列(综合提升篇) 专题02 概率统计解答题(理)福建省莆田市仙游第一中学2018-2019学年高三上学期月考数学(理)试题



