约数,又称因数.它的定义如下:若整数 除以整数
除以整数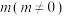 除得的商正好是整数而没有余数,我们就称
除得的商正好是整数而没有余数,我们就称 为
为 的倍数,称
的倍数,称 为
为 的约数.设正整数
的约数.设正整数 共有
共有 个正约数,记为
个正约数,记为 ,
, ,…,
,…,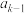 ,
,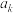 (
(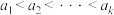 ).
).
(1)当 时,若正整数
时,若正整数 的
的 个正约数构成等比数列,请写出一个
个正约数构成等比数列,请写出一个 的值;
的值;
(2)当 时,若
时,若 ,
, ,…,
,…, 构成等比数列,求证:
构成等比数列,求证: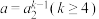 ;
;
(3)记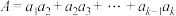 ,求证:
,求证: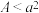 .
.
 除以整数
除以整数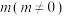 除得的商正好是整数而没有余数,我们就称
除得的商正好是整数而没有余数,我们就称 为
为 的倍数,称
的倍数,称 为
为 的约数.设正整数
的约数.设正整数 共有
共有 个正约数,记为
个正约数,记为 ,
, ,…,
,…,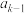 ,
,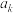 (
(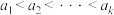 ).
).(1)当
 时,若正整数
时,若正整数 的
的 个正约数构成等比数列,请写出一个
个正约数构成等比数列,请写出一个 的值;
的值;(2)当
 时,若
时,若 ,
, ,…,
,…, 构成等比数列,求证:
构成等比数列,求证: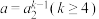 ;
;(3)记
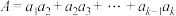 ,求证:
,求证: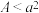 .
.
2024·广东惠州·一模 查看更多[4]
广东省惠州市2024届高三下学期模拟考试(一模)数学试题(已下线)广东省阳江市2024届高三下学期5月模拟数学试题广东省江门市新会第一中学2024届高三下学期高考热身考试数学试题(已下线)专题7 线性代数、抽象代数与数论背景的新定义压轴大题(一)【讲】
更新时间:2024/05/14 16:34:42
|
相似题推荐
解答题-证明题
|
困难
(0.15)
【推荐1】对于数列 ,若存在常数
,若存在常数 ,
,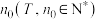 ,使得对任意的正整数
,使得对任意的正整数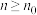 ,恒有
,恒有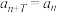 成立,则称数列
成立,则称数列 是从第
是从第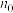 项起的周期为
项起的周期为 的周期数列.当
的周期数列.当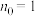 时,称数列
时,称数列 为纯周期数列;当
为纯周期数列;当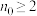 时,称数列
时,称数列 为混周期数列.记
为混周期数列.记 为不超过
为不超过 的最大整数,设各项均为正整数的数列
的最大整数,设各项均为正整数的数列 满足:
满足: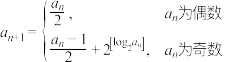 .
.
(1)若对任意正整数 都有
都有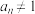 ,请写出三个满足条件的
,请写出三个满足条件的 的值;
的值;
(2)若数列 是纯周期数列,请写出满足条件的
是纯周期数列,请写出满足条件的 的表达式,并说明理由;
的表达式,并说明理由;
(3)证明:不论 为何值,总存在
为何值,总存在 使得
使得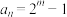 .
.
 ,若存在常数
,若存在常数 ,
,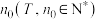 ,使得对任意的正整数
,使得对任意的正整数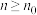 ,恒有
,恒有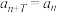 成立,则称数列
成立,则称数列 是从第
是从第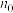 项起的周期为
项起的周期为 的周期数列.当
的周期数列.当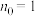 时,称数列
时,称数列 为纯周期数列;当
为纯周期数列;当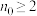 时,称数列
时,称数列 为混周期数列.记
为混周期数列.记 为不超过
为不超过 的最大整数,设各项均为正整数的数列
的最大整数,设各项均为正整数的数列 满足:
满足: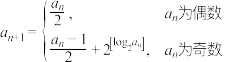 .
.(1)若对任意正整数
 都有
都有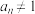 ,请写出三个满足条件的
,请写出三个满足条件的 的值;
的值;(2)若数列
 是纯周期数列,请写出满足条件的
是纯周期数列,请写出满足条件的 的表达式,并说明理由;
的表达式,并说明理由;(3)证明:不论
 为何值,总存在
为何值,总存在 使得
使得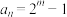 .
.
您最近一年使用:0次
解答题-问答题
|
困难
(0.15)
解题方法
【推荐2】用 表示一个小于或等于
表示一个小于或等于 的最大整数.如:
的最大整数.如: ,
,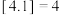 ,
,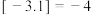 . 已知实数列
. 已知实数列 、
、 、
、 对于所有非负整数
对于所有非负整数 满足
满足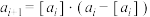 ,其中
,其中 是任意一个非零实数.
是任意一个非零实数.
(Ⅰ)若 ,写出
,写出 、
、 、
、 ;
;
(Ⅱ)若 ,求数列
,求数列 的最小值;
的最小值;
(Ⅲ)证明:存在非负整数 ,使得当
,使得当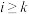 时,
时,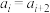 .
.
 表示一个小于或等于
表示一个小于或等于 的最大整数.如:
的最大整数.如: ,
,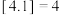 ,
,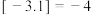 . 已知实数列
. 已知实数列 、
、 、
、 对于所有非负整数
对于所有非负整数 满足
满足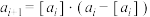 ,其中
,其中 是任意一个非零实数.
是任意一个非零实数.(Ⅰ)若
 ,写出
,写出 、
、 、
、 ;
;(Ⅱ)若
 ,求数列
,求数列 的最小值;
的最小值;(Ⅲ)证明:存在非负整数
 ,使得当
,使得当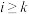 时,
时,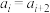 .
.
您最近一年使用:0次
解答题-应用题
|
困难
(0.15)
名校
【推荐3】生命的诞生与流逝是一个永恒的话题,就某种细胞而言,由该种细胞的一个个体进行分裂,分裂后成为新细胞而原细胞不复存在,多次分裂后,由该个细胞繁殖而来的全部细胞均死亡,我们称该细胞“灭绝”.现已知某种细胞有 的概率分裂为
的概率分裂为 个细胞(即死亡),...,有
个细胞(即死亡),...,有 的概率分裂为
的概率分裂为 个细胞.记事件
个细胞.记事件 :细胞最终灭绝,
:细胞最终灭绝, :细胞第一次分裂为
:细胞第一次分裂为 个细胞.记该细胞第一次分裂后有
个细胞.记该细胞第一次分裂后有 个个体(分裂后的细胞互不影响),在概率论中,我们用
个个体(分裂后的细胞互不影响),在概率论中,我们用 的数学期望
的数学期望 作为衡量生物灭绝可能性的依据,如果
作为衡量生物灭绝可能性的依据,如果 ,则在理论上细胞就不会灭绝;相反,如果
,则在理论上细胞就不会灭绝;相反,如果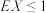 ,则理论上我们认为细胞在足够多代的繁殖后会灭绝,而这两种情况在生物界中都是普遍存在的.
,则理论上我们认为细胞在足够多代的繁殖后会灭绝,而这两种情况在生物界中都是普遍存在的.
(1)直接写出 的数学期望
的数学期望 .
.
(2)用只含 和
和 的概率式表示
的概率式表示 并证明该细胞灭绝的概率为关于
并证明该细胞灭绝的概率为关于 方程:
方程: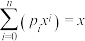 的最小正实根.
的最小正实根.
(3)若某种细胞发生基因突变,当 时
时 .
.
(ⅰ)若当其分裂为两个细胞后,有一个细胞具有与原细胞相同的活力,而另一细胞则在此后丧失分裂为两个的能力(即只有可能分裂成 个或
个或 个),求证:该细胞的灭绝是必然事件.
个),求证:该细胞的灭绝是必然事件.
(ⅱ)受某种辐射污染,若当其分裂为两个细胞后分裂生成的两个细胞此后均丧失分裂为 个的能力,并等可能分裂为
个的能力,并等可能分裂为 个或
个或 个细胞.我们称为“泛滥型细胞”,已知:
个细胞.我们称为“泛滥型细胞”,已知: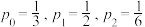 ,求出一个该种泛滥型细胞经过
,求出一个该种泛滥型细胞经过 次分裂,得到
次分裂,得到 个细胞的概率
个细胞的概率 .
.
 的概率分裂为
的概率分裂为 个细胞(即死亡),...,有
个细胞(即死亡),...,有 的概率分裂为
的概率分裂为 个细胞.记事件
个细胞.记事件 :细胞最终灭绝,
:细胞最终灭绝, :细胞第一次分裂为
:细胞第一次分裂为 个细胞.记该细胞第一次分裂后有
个细胞.记该细胞第一次分裂后有 个个体(分裂后的细胞互不影响),在概率论中,我们用
个个体(分裂后的细胞互不影响),在概率论中,我们用 的数学期望
的数学期望 作为衡量生物灭绝可能性的依据,如果
作为衡量生物灭绝可能性的依据,如果 ,则在理论上细胞就不会灭绝;相反,如果
,则在理论上细胞就不会灭绝;相反,如果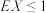 ,则理论上我们认为细胞在足够多代的繁殖后会灭绝,而这两种情况在生物界中都是普遍存在的.
,则理论上我们认为细胞在足够多代的繁殖后会灭绝,而这两种情况在生物界中都是普遍存在的.(1)直接写出
 的数学期望
的数学期望 .
.(2)用只含
 和
和 的概率式表示
的概率式表示 并证明该细胞灭绝的概率为关于
并证明该细胞灭绝的概率为关于 方程:
方程: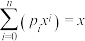 的最小正实根.
的最小正实根.(3)若某种细胞发生基因突变,当
 时
时 .
.(ⅰ)若当其分裂为两个细胞后,有一个细胞具有与原细胞相同的活力,而另一细胞则在此后丧失分裂为两个的能力(即只有可能分裂成
 个或
个或 个),求证:该细胞的灭绝是必然事件.
个),求证:该细胞的灭绝是必然事件.(ⅱ)受某种辐射污染,若当其分裂为两个细胞后分裂生成的两个细胞此后均丧失分裂为
 个的能力,并等可能分裂为
个的能力,并等可能分裂为 个或
个或 个细胞.我们称为“泛滥型细胞”,已知:
个细胞.我们称为“泛滥型细胞”,已知: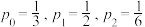 ,求出一个该种泛滥型细胞经过
,求出一个该种泛滥型细胞经过 次分裂,得到
次分裂,得到 个细胞的概率
个细胞的概率 .
.
您最近一年使用:0次
【推荐1】已知 ,
,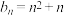 ,函数
,函数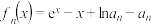 .
.
(1)若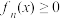 ,求
,求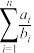 ;
;
(2)设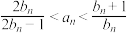 .记M为
.记M为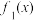 ,
,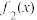 ,…,
,…,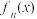 的所有零点组成的集合,X,Y为M的子集,它们各有n个元素,且
的所有零点组成的集合,X,Y为M的子集,它们各有n个元素,且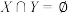 .设
.设 ,
,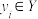 ,
, ,2,…,n,且
,2,…,n,且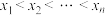 ,
,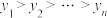 .证明:
.证明:
(i)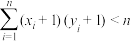 ;
;
(ii)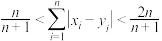 .
.
 ,
,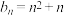 ,函数
,函数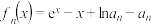 .
.(1)若
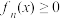 ,求
,求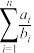 ;
;(2)设
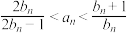 .记M为
.记M为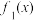 ,
,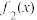 ,…,
,…,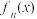 的所有零点组成的集合,X,Y为M的子集,它们各有n个元素,且
的所有零点组成的集合,X,Y为M的子集,它们各有n个元素,且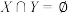 .设
.设 ,
,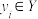 ,
, ,2,…,n,且
,2,…,n,且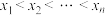 ,
,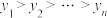 .证明:
.证明:(i)
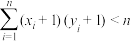 ;
;(ii)
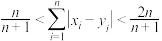 .
.
您最近一年使用:0次
解答题-问答题
|
困难
(0.15)
名校
【推荐2】已知数列{an}的前n项和 .
.
(1)求数列{an}的通项公式an;
(2)设数列{bn}的前n项和为Tn,满足b1=1,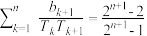 .
.
①求数列{bn}的通项公式bn;
②若存在p,q,k∈N*,p<q<k,使得ambq,amanbp,anbk成等差数列,求m+n的最小值.
 .
.(1)求数列{an}的通项公式an;
(2)设数列{bn}的前n项和为Tn,满足b1=1,
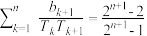 .
.①求数列{bn}的通项公式bn;
②若存在p,q,k∈N*,p<q<k,使得ambq,amanbp,anbk成等差数列,求m+n的最小值.
您最近一年使用:0次
【推荐1】已知数列 满足
满足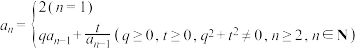 .
.
(1)当 时,求证:数列
时,求证:数列 不可能是常数列;
不可能是常数列;
(2)若 ,求数列
,求数列 的前
的前 项的和;
项的和;
(3)当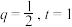 时,令
时,令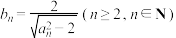 ,判断对任意
,判断对任意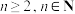 ,
, 是否为正整数,请说明理由.
是否为正整数,请说明理由.
 满足
满足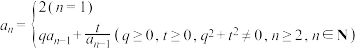 .
.(1)当
 时,求证:数列
时,求证:数列 不可能是常数列;
不可能是常数列;(2)若
 ,求数列
,求数列 的前
的前 项的和;
项的和;(3)当
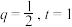 时,令
时,令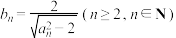 ,判断对任意
,判断对任意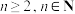 ,
, 是否为正整数,请说明理由.
是否为正整数,请说明理由.
您最近一年使用:0次
【推荐2】已知各项均不为0的数列 满足
满足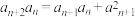 (
( 是正整数),
是正整数),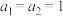 ,定义函数
,定义函数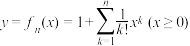 ,
, 是自然对数的底数.
是自然对数的底数.
(1)求证:数列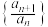 是等差数列,并求数列
是等差数列,并求数列 的通项公式;
的通项公式;
(2)记函数 ,其中
,其中 .
.
(i)证明:对任意 ,
, ;
;
(ii)数列 满足
满足 ,设
,设 为数列
为数列 的前
的前 项和.数列
项和.数列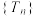 的极限的严格定义为:若存在一个常数
的极限的严格定义为:若存在一个常数 ,使得对任意给定的正实数
,使得对任意给定的正实数 (不论它多么小),总存在正整数m满足:当
(不论它多么小),总存在正整数m满足:当 时,恒有
时,恒有 成立,则称
成立,则称 为数列
为数列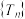 的极限.试根据以上定义求出数列
的极限.试根据以上定义求出数列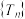 的极限
的极限 .
.
 满足
满足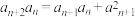 (
( 是正整数),
是正整数),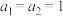 ,定义函数
,定义函数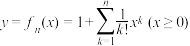 ,
, 是自然对数的底数.
是自然对数的底数.(1)求证:数列
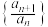 是等差数列,并求数列
是等差数列,并求数列 的通项公式;
的通项公式;(2)记函数
 ,其中
,其中 .
.(i)证明:对任意
 ,
, ;
;(ii)数列
 满足
满足 ,设
,设 为数列
为数列 的前
的前 项和.数列
项和.数列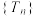 的极限的严格定义为:若存在一个常数
的极限的严格定义为:若存在一个常数 ,使得对任意给定的正实数
,使得对任意给定的正实数 (不论它多么小),总存在正整数m满足:当
(不论它多么小),总存在正整数m满足:当 时,恒有
时,恒有 成立,则称
成立,则称 为数列
为数列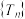 的极限.试根据以上定义求出数列
的极限.试根据以上定义求出数列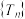 的极限
的极限 .
.
您最近一年使用:0次
解答题-问答题
|
困难
(0.15)
名校
解题方法
【推荐1】差分密码分析(Differential Cryptanalysis)是一种密码分析方法,旨在通过观察密码算法在不同输入差分下产生的输出差分,来推断出密码算法的密钥信息.对于数列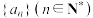 ,规定
,规定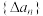 为数列
为数列 的一阶差分数列,其中
的一阶差分数列,其中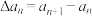 ;规定
;规定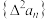 为
为 的二阶差分数列,其中
的二阶差分数列,其中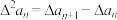 .如果
.如果 的一阶差分数列满足
的一阶差分数列满足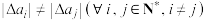 ,则称
,则称 是“绝对差异数列”;如果
是“绝对差异数列”;如果 的二阶差分数列满足
的二阶差分数列满足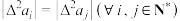 ,则称
,则称 是“累差不变数列”.
是“累差不变数列”.
(1)设数列 ,判断数列
,判断数列 是否为“绝对差异数列”或“累差不变数列”,请说明理由;
是否为“绝对差异数列”或“累差不变数列”,请说明理由;
(2)设数列 的通项公式
的通项公式 ,分别判断
,分别判断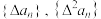 是否为等差数列,请说明理由;
是否为等差数列,请说明理由;
(3)设各项均为正数的数列 为“累差不变数列”,其前
为“累差不变数列”,其前 项和为
项和为 ,且对
,且对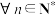 ,都有
,都有 ,对满足
,对满足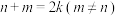 的任意正整数
的任意正整数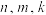 都有
都有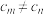 ,且不等式
,且不等式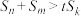 恒成立,求实数
恒成立,求实数 的最大值.
的最大值.
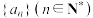 ,规定
,规定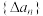 为数列
为数列 的一阶差分数列,其中
的一阶差分数列,其中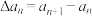 ;规定
;规定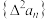 为
为 的二阶差分数列,其中
的二阶差分数列,其中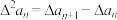 .如果
.如果 的一阶差分数列满足
的一阶差分数列满足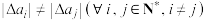 ,则称
,则称 是“绝对差异数列”;如果
是“绝对差异数列”;如果 的二阶差分数列满足
的二阶差分数列满足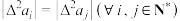 ,则称
,则称 是“累差不变数列”.
是“累差不变数列”.(1)设数列
 ,判断数列
,判断数列 是否为“绝对差异数列”或“累差不变数列”,请说明理由;
是否为“绝对差异数列”或“累差不变数列”,请说明理由;(2)设数列
 的通项公式
的通项公式 ,分别判断
,分别判断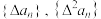 是否为等差数列,请说明理由;
是否为等差数列,请说明理由;(3)设各项均为正数的数列
 为“累差不变数列”,其前
为“累差不变数列”,其前 项和为
项和为 ,且对
,且对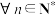 ,都有
,都有 ,对满足
,对满足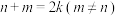 的任意正整数
的任意正整数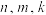 都有
都有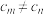 ,且不等式
,且不等式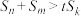 恒成立,求实数
恒成立,求实数 的最大值.
的最大值.
您最近一年使用:0次
【推荐2】已知数列 是正项等比数列,
是正项等比数列, 是等差数列,且
是等差数列,且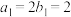 ,
, ,
, ,
,
(1)求数列 和
和 的通项公式;
的通项公式;
(2) 表示不超过x的最大整数,
表示不超过x的最大整数, 表示数列
表示数列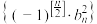 的前
的前 项和,集合
项和,集合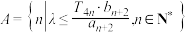 共有4个元素,求
共有4个元素,求 范围;
范围;
(3) ,数列
,数列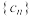 的前
的前 项和为
项和为 ,求证:
,求证: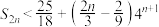 .
.
 是正项等比数列,
是正项等比数列, 是等差数列,且
是等差数列,且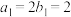 ,
, ,
, ,
,(1)求数列
 和
和 的通项公式;
的通项公式;(2)
 表示不超过x的最大整数,
表示不超过x的最大整数, 表示数列
表示数列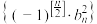 的前
的前 项和,集合
项和,集合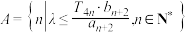 共有4个元素,求
共有4个元素,求 范围;
范围;(3)
 ,数列
,数列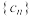 的前
的前 项和为
项和为 ,求证:
,求证: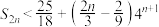 .
.
您最近一年使用:0次

 .
. 的极值;
的极值;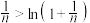 ;
; ,求整数a,使得
,求整数a,使得 .
.
 的项
的项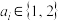 ,其中
,其中 …,
…, ,
, ,其前
,其前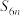 ,记
,记 的值;
的值; ,
, 中,
中, ,
,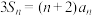 ,
, .
.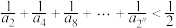 ;
;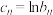 ,
, ,求证:
,求证: .
.


