已知数列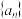 有
有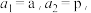 (常数p>0),对任意的正整数n,Sn=a1+a2+…+an,
(常数p>0),对任意的正整数n,Sn=a1+a2+…+an,
并有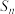 满足
满足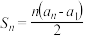 .
.
(I)试判断数列 是否是等差数列,若是,求其通项公式,若不是,说明理由;
是否是等差数列,若是,求其通项公式,若不是,说明理由;
(II)令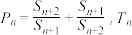 是数列
是数列 的前n项和,求证:Tn﹣2n<3.
的前n项和,求证:Tn﹣2n<3.
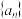 有
有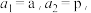 (常数p>0),对任意的正整数n,Sn=a1+a2+…+an,
(常数p>0),对任意的正整数n,Sn=a1+a2+…+an,并有
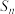 满足
满足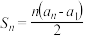 .
.(I)试判断数列
 是否是等差数列,若是,求其通项公式,若不是,说明理由;
是否是等差数列,若是,求其通项公式,若不是,说明理由;(II)令
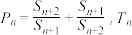 是数列
是数列 的前n项和,求证:Tn﹣2n<3.
的前n项和,求证:Tn﹣2n<3.
11-12高三·山东潍坊·阶段练习 查看更多[1]
(已下线)2012届山东省青州市高三2月月考理科数学
更新时间:2016/12/01 15:45:08
|
相似题推荐
解答题-证明题
|
适中
(0.65)
【推荐1】设数列{an}的前n项和为Sn,点P(Sn,an)在直线(3﹣m)x+2my﹣m﹣3=0上,(m∈N*,m为常数,m≠3);
(1)求an;
(2)若数列{an}的公比q=f(m),数列{bn}满足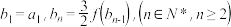 ,求证:
,求证: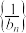 为等差数列,并求bn;
为等差数列,并求bn;
(3)设数列{cn}满足cn=bn•bn+2,Tn为数列{cn}的前n项和,且存在实数T满足Tn≥T,(n∈N*),求T的最大值.
(1)求an;
(2)若数列{an}的公比q=f(m),数列{bn}满足
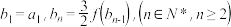 ,求证:
,求证: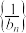 为等差数列,并求bn;
为等差数列,并求bn;(3)设数列{cn}满足cn=bn•bn+2,Tn为数列{cn}的前n项和,且存在实数T满足Tn≥T,(n∈N*),求T的最大值.
您最近一年使用:0次
解答题-问答题
|
适中
(0.65)
【推荐2】已知数列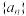 的各项均为正数,其前
的各项均为正数,其前 项和为
项和为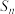 ,且
,且 与
与 的等差中项等于
的等差中项等于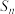 与
与 的等比中项.
的等比中项.
(1)求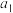 的值及数列
的值及数列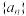 的通项公式;
的通项公式;
(2)设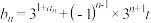 ,对
,对 有
有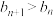 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
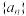 的各项均为正数,其前
的各项均为正数,其前 项和为
项和为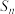 ,且
,且 与
与 的等差中项等于
的等差中项等于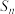 与
与 的等比中项.
的等比中项.(1)求
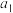 的值及数列
的值及数列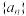 的通项公式;
的通项公式;(2)设
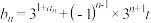 ,对
,对 有
有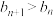 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
解答题-问答题
|
适中
(0.65)
解题方法
【推荐1】在数列 ,
, 中,已知
中,已知 ,且
,且 .
.
(Ⅰ)求数列 和
和 的通项公式;
的通项公式;
(Ⅱ)求数列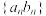 的前
的前 项和
项和 .
.
 ,
, 中,已知
中,已知 ,且
,且 .
.(Ⅰ)求数列
 和
和 的通项公式;
的通项公式;(Ⅱ)求数列
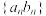 的前
的前 项和
项和 .
.
您最近一年使用:0次
解答题-问答题
|
适中
(0.65)
解题方法
【推荐2】已知数列 的前
的前 项和为
项和为 ,且
,且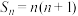 ,
,
(1)求数列 的通项公式
的通项公式 ;
;
(2)数列 的通项公式
的通项公式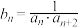 ,求数列
,求数列 的前
的前 项和
项和 .
.
 的前
的前 项和为
项和为 ,且
,且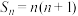 ,
,(1)求数列
 的通项公式
的通项公式 ;
;(2)数列
 的通项公式
的通项公式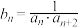 ,求数列
,求数列 的前
的前 项和
项和 .
.
您最近一年使用:0次
解答题-问答题
|
适中
(0.65)
名校
【推荐1】已知等比数列 满足,
满足,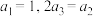 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若等差数列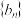 的前
的前 项和为
项和为 ,满足
,满足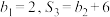 ,求数列
,求数列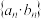 的前项和
的前项和 .
.
 满足,
满足,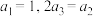 .
.(1)求数列
 的通项公式;
的通项公式;(2)若等差数列
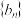 的前
的前 项和为
项和为 ,满足
,满足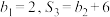 ,求数列
,求数列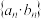 的前项和
的前项和 .
.
您最近一年使用:0次
【推荐2】已知数列 满足:
满足: ,
,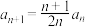 .
.
(1)求数列 的通项公式;
的通项公式;
(2)求数列 前n项和
前n项和 ;
;
(3)若集合 为空集,求实数
为空集,求实数 的取值范围.
的取值范围.
 满足:
满足: ,
,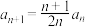 .
.(1)求数列
 的通项公式;
的通项公式;(2)求数列
 前n项和
前n项和 ;
;(3)若集合
 为空集,求实数
为空集,求实数 的取值范围.
的取值范围.
您最近一年使用:0次

 ,且
,且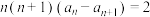 ,其中
,其中 .
.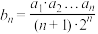 ,求数列
,求数列 的前n项和为
的前n项和为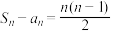 .
.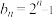 ,求数列
,求数列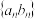 的前n项和
的前n项和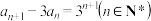 .
.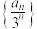 是等差数列,并求数列
是等差数列,并求数列

