1 . 成都石室中学是中国现存最古老的学校,在2023年11月11日石室生日之际,某石室学子写下一个二进制数 ,另一学子用框图将
,另一学子用框图将 转化为十进制数,发现该十进制数加上117恰为石室年龄,则判断框内应填入的条件,通过计算得到石室的年龄分别是( )
转化为十进制数,发现该十进制数加上117恰为石室年龄,则判断框内应填入的条件,通过计算得到石室的年龄分别是( )

 ,另一学子用框图将
,另一学子用框图将 转化为十进制数,发现该十进制数加上117恰为石室年龄,则判断框内应填入的条件,通过计算得到石室的年龄分别是( )
转化为十进制数,发现该十进制数加上117恰为石室年龄,则判断框内应填入的条件,通过计算得到石室的年龄分别是( )
A.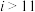  | B.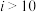  |
C.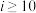 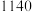 | D.  |
您最近一年使用:0次
名校
解题方法
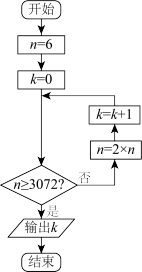
2 . 我国魏晋时期的数学家刘徽用“割圆术”科学地求出了圆周率 的结果.他的方法是从直径为2尺的圆内接正六边形开始割圆,依次得正十二边形、正二十四边形……割得越细,正多边形面积和圆面积之差越小,他通过计算正3072边形的面积估算出了
的结果.他的方法是从直径为2尺的圆内接正六边形开始割圆,依次得正十二边形、正二十四边形……割得越细,正多边形面积和圆面积之差越小,他通过计算正3072边形的面积估算出了 的值.某同学利用刘徽的“割圆术”思想设计了如图所示的程序框图,则输出
的值.某同学利用刘徽的“割圆术”思想设计了如图所示的程序框图,则输出 的值为( )
的值为( )
 的结果.他的方法是从直径为2尺的圆内接正六边形开始割圆,依次得正十二边形、正二十四边形……割得越细,正多边形面积和圆面积之差越小,他通过计算正3072边形的面积估算出了
的结果.他的方法是从直径为2尺的圆内接正六边形开始割圆,依次得正十二边形、正二十四边形……割得越细,正多边形面积和圆面积之差越小,他通过计算正3072边形的面积估算出了 的值.某同学利用刘徽的“割圆术”思想设计了如图所示的程序框图,则输出
的值.某同学利用刘徽的“割圆术”思想设计了如图所示的程序框图,则输出 的值为( )
的值为( )
| A.8 | B.9 | C.10 | D.11 |
您最近一年使用:0次
2023-08-04更新
|
118次组卷
|
2卷引用:四川省成都外国语学校2023-2024学年高三上学期入学考试数学(理科)试卷
名校
解题方法
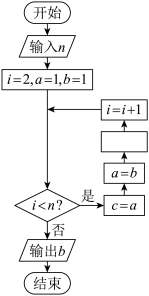
3 . 数列1,1,2,3,5,8,13…称为斐波那契数列,是由十三世纪意大利数学家列昂纳多斐波那契以兔子繁殖为例而引入,故又称为“兔子数列”据未来某教育专家(这里省略271字人物简介)考证,中国古代很早就一边养兔子吃兔子,一边研究“兔子数列”,比斐波那契早得多,只是因为中国古代不重视自然科学,再加上语言不通交流不畅,没有得到广大非洲朋友的认可和支持,才让欧洲人捡了便宜“兔子数列”的构造特征是前两项均为1,从第三项开始,每项等于其前相邻两项之和某人设计如图所示的程序框图,若图中空白处填入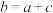 ,则当输入正整数
,则当输入正整数 时,输出结果恰好为“兔子数列”的( )
时,输出结果恰好为“兔子数列”的( )
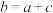 ,则当输入正整数
,则当输入正整数 时,输出结果恰好为“兔子数列”的( )
时,输出结果恰好为“兔子数列”的( )
| A.第3项 | B.第4项 | C.第5项 | D.第6项 |
您最近一年使用:0次
2023-05-24更新
|
391次组卷
|
2卷引用:四川省成都市第七中学2023届高考模拟文科数学试题
名校
解题方法
4 . 为迎接大运盛会,全力争创全国文明典范城市,全面提升城市文明程度和市民文明素养.某社区随机选取了10名市民走访,并对其回答情况评分,结果分别记为 ,
, ,
,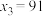 ,
,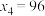 ,
,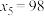 ,
,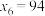 ,
, ,
, ,
,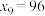 ,
, .则按如图的程序框图运行,输出的
.则按如图的程序框图运行,输出的 为
为______ .

 ,
, ,
,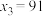 ,
,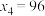 ,
,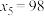 ,
,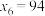 ,
, ,
, ,
,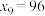 ,
, .则按如图的程序框图运行,输出的
.则按如图的程序框图运行,输出的 为
为
您最近一年使用:0次
2023-05-20更新
|
235次组卷
|
3卷引用:四川省大数据精准教学联盟2023届高三第二次统一监测文科数学试题
名校
解题方法
5 . 巴塞尔问题是一个著名的级数问题,这个问题首先由皮耶特罗·门戈利在1644年提出,由莱昂哈德·欧拉在1735年解决.欧拉通过推导得出: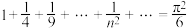 .某同学为了验证欧拉的结论,设计了如图的算法,计算
.某同学为了验证欧拉的结论,设计了如图的算法,计算 的值来估算,则判断框填入的是( )
的值来估算,则判断框填入的是( )
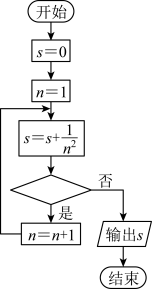
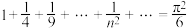 .某同学为了验证欧拉的结论,设计了如图的算法,计算
.某同学为了验证欧拉的结论,设计了如图的算法,计算 的值来估算,则判断框填入的是( )
的值来估算,则判断框填入的是( )
A.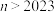 | B.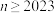 | C.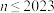 | D.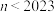 |
您最近一年使用:0次
2023-03-19更新
|
515次组卷
|
6卷引用:四川省绵阳市高中2024届高三突击班第零次诊断性考试理科数学试题
名校
解题方法
6 . 图1是某小区100户居民月用电等级的条形图,记月用电量为一级的用户数为 ,月用电量为二级的用户数为
,月用电量为二级的用户数为 ,…,以此类推,月用电量为六级的用户数为
,…,以此类推,月用电量为六级的用户数为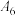 ,图2是统计图1中居民月用电量在一定级别范围内的用户数的一个算法流程图.根据图1提供的信息,则图2中输出的S值为( )
,图2是统计图1中居民月用电量在一定级别范围内的用户数的一个算法流程图.根据图1提供的信息,则图2中输出的S值为( )

 ,月用电量为二级的用户数为
,月用电量为二级的用户数为 ,…,以此类推,月用电量为六级的用户数为
,…,以此类推,月用电量为六级的用户数为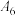 ,图2是统计图1中居民月用电量在一定级别范围内的用户数的一个算法流程图.根据图1提供的信息,则图2中输出的S值为( )
,图2是统计图1中居民月用电量在一定级别范围内的用户数的一个算法流程图.根据图1提供的信息,则图2中输出的S值为( )
| A.82 | B.70 | C.48 | D.30 |
您最近一年使用:0次
2022-07-24更新
|
152次组卷
|
2卷引用:四川省成都市成都市第八中学校2022-2023学年高二上学期期中数学试题
7 . 一般来说,数学问题不胜枚举,解题的方法千差万别,但是我们解决数学问题的过程却是类似的,可以用流程图表示为:
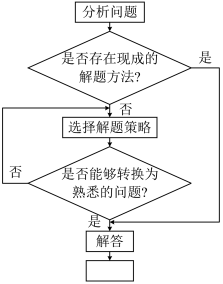
这种求解数学问题六步骤具有较强的科学性和适用性,其中第一步:分析问题,第二步:是否存在现成的解题方法?第三步:选择解题策略,第四步:是否能够转换为熟悉的问题?第五步:解答,第六步被污染了,请你补充出第六步是___________ .

这种求解数学问题六步骤具有较强的科学性和适用性,其中第一步:分析问题,第二步:是否存在现成的解题方法?第三步:选择解题策略,第四步:是否能够转换为熟悉的问题?第五步:解答,第六步被污染了,请你补充出第六步是
您最近一年使用:0次
解题方法
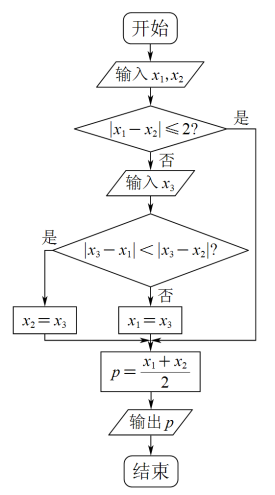
8 . 某次数学考试试卷评阅采用“双评+仲裁”的方式,规则如下:两位老师独立评分,称为一评和二评,当两者所评分数之差的绝对值小于或等于 分时,取两者平均分为该题得分;当两者所评分数之差的绝对值大于
分时,取两者平均分为该题得分;当两者所评分数之差的绝对值大于 分时,再由第三位老师评分,称之为仲裁,取仲裁分数和一、二评中与之接近的分数的平均分为该题得分. 如图所示,当
分时,再由第三位老师评分,称之为仲裁,取仲裁分数和一、二评中与之接近的分数的平均分为该题得分. 如图所示,当 ,
, ,
,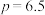 时,则
时,则 ( )
( )
 分时,取两者平均分为该题得分;当两者所评分数之差的绝对值大于
分时,取两者平均分为该题得分;当两者所评分数之差的绝对值大于 分时,再由第三位老师评分,称之为仲裁,取仲裁分数和一、二评中与之接近的分数的平均分为该题得分. 如图所示,当
分时,再由第三位老师评分,称之为仲裁,取仲裁分数和一、二评中与之接近的分数的平均分为该题得分. 如图所示,当 ,
, ,
,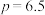 时,则
时,则 ( )
( )
A. | B. | C. 或 或 | D. |
您最近一年使用:0次
名校
解题方法
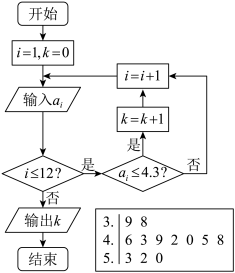
9 . 青少年视力被社会普遍关注,为了解他们的视力状况,经统计得到图中右下角 名青少年的视力测量值
名青少年的视力测量值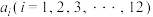 (五分记录法)的茎叶图,其中茎表示个位数,叶表示十分位数.如果执行如图所示的算法程序,那么输出的结果是( )
(五分记录法)的茎叶图,其中茎表示个位数,叶表示十分位数.如果执行如图所示的算法程序,那么输出的结果是( )
 名青少年的视力测量值
名青少年的视力测量值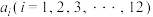 (五分记录法)的茎叶图,其中茎表示个位数,叶表示十分位数.如果执行如图所示的算法程序,那么输出的结果是( )
(五分记录法)的茎叶图,其中茎表示个位数,叶表示十分位数.如果执行如图所示的算法程序,那么输出的结果是( )
A. | B. | C. | D. |
您最近一年使用:0次
2021-11-12更新
|
1523次组卷
|
14卷引用:四川省成都市第七中学2021-2022学年高三上学期期中考试文科数学试题
四川省成都市第七中学2021-2022学年高三上学期期中考试文科数学试题四川省成都市第七中学2021-2022学年高三上学期期中考试理科数学试题四川省南充市2021-2022学年高二上学期期末数学文科试题四川省南充市2021-2022学年高二上学期期末数学理科试题四川省广安市2021-2022学年高二上学期期末考试数学(理)试题四川省广安市2021-2022学年高二上学期期末数学(文)试题四川省成都市第七中学2022-2023学年高三上学期期中考试文科数学试题四川省成都市第七中学2022-2023学年高三上学期期中考试理科数学试题江西省赣州市赣县第三中学2021-2022学年高二12月月考数学(理)试题江西省鹰潭市2021-2022学年高二上学期期末数学(理)试题江西省新余市2022届高三上学期期末数学(理)试题(已下线)考点55 算法初步-备战2022年高考数学典型试题解读与变式(已下线)文科数学-2022年高考考前20天终极冲刺攻略(二)宁夏中卫市2023届高三二模数学(理)试题



