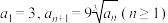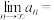1 . 如图,将 个整数放入
个整数放入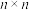 的宫格中,使得任意一行及任意一列的乘积为2或-2,记将
的宫格中,使得任意一行及任意一列的乘积为2或-2,记将 个整数放入
个整数放入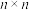 的宫格有
的宫格有 种放法,则
种放法,则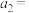
______ ,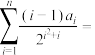
______ .
 个整数放入
个整数放入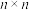 的宫格中,使得任意一行及任意一列的乘积为2或-2,记将
的宫格中,使得任意一行及任意一列的乘积为2或-2,记将 个整数放入
个整数放入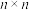 的宫格有
的宫格有 种放法,则
种放法,则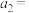

您最近一年使用:0次
2024-01-10更新
|
568次组卷
|
4卷引用:辽宁省辽阳市2024届高三上学期期末数学试题
辽宁省辽阳市2024届高三上学期期末数学试题(已下线)第六章 计数原理(单元重点综合测试)-2023-2024学年高二数学单元速记·巧练(沪教版2020选择性必修第二册)(已下线)新题型02 新高考新结构竞赛题型十五大考点汇总-2广东省部分学校2023-2024学年高三上学期12月月考数学试题
2 . 已知数列 的前
的前 项和
项和 满足
满足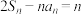 ,
,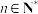 ,且
,且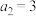 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设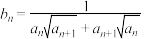 ,
, 为数列
为数列 的前
的前 项和,求使
项和,求使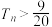 成立的最小正整数
成立的最小正整数 的值.
的值.
 的前
的前 项和
项和 满足
满足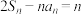 ,
,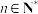 ,且
,且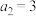 .
.(1)求数列
 的通项公式;
的通项公式;(2)设
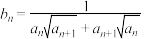 ,
, 为数列
为数列 的前
的前 项和,求使
项和,求使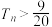 成立的最小正整数
成立的最小正整数 的值.
的值.
您最近一年使用:0次
2019-01-28更新
|
970次组卷
|
7卷引用:高二下学期期末押题卷01
(已下线)高二下学期期末押题卷012018年全国高中数学联赛福建省预赛江西省宜丰中学、宜春一中、万载中学2021届高三3月联考数学(理)试题(已下线)2021年高考数学押题预测卷(新高考卷)01湖南省株洲市第二中学2021-2022学年高二下学期“同济大学”杯数理化联赛数学试题山西省运城中学校2022届高三冲刺模拟(一)数学(文)试题广东省高州中学2022-2023学年高二下学期期中数学试题
3 . 已知数列 前
前 项和为
项和为 且对任意正整数
且对任意正整数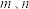 ,均有
,均有 若
若 对任意的
对任意的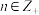 恒成立,则实数
恒成立,则实数 的最小值为
的最小值为______ .
 前
前 项和为
项和为 且对任意正整数
且对任意正整数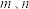 ,均有
,均有 若
若 对任意的
对任意的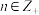 恒成立,则实数
恒成立,则实数 的最小值为
的最小值为
您最近一年使用:0次
2018-12-06更新
|
455次组卷
|
11卷引用:广东省中山市2018届高三上学期期末考试数学(理)试题
广东省中山市2018届高三上学期期末考试数学(理)试题广东省中山市2018届高三上学期期末考试数学(文)试题上海市金山中学2018-2019学年高一下学期期末考试数学试题人教版高中数学 高三二轮 专题13 等差数列 等比数列问题黑龙江省大庆实验中学2017-2018学年高一4月月考数学(理)试题2015年全国高中数学联赛辽宁赛区预赛试题智能测评与辅导[理]-数列的综合应用(已下线)第03讲 等比数列及其前n项和(讲)-《2020年高考一轮复习讲练测》(浙江版)上海市十四校(原十三校)2016-2017学年高三上学期12月联考数学试题江苏省无锡市宜兴市第二高级中学2020-2021学年高二上学期第一次基础检测数学试题(已下线)专题7.3 等比数列及其前n项和(讲)-2021年新高考数学一轮复习讲练测
13-14高一·湖北襄阳·期末
名校
4 . 已知数列 满足
满足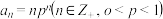 .对于说法:
.对于说法:
①当 时,数列
时,数列 为递减数列;
为递减数列;
②当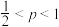 时,数列
时,数列 不一定有最大项;
不一定有最大项;
③当 时,数列
时,数列 为递减数列;
为递减数列;
④当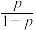 为正整数时,数列
为正整数时,数列 必有两项相等的最大项,
必有两项相等的最大项,
正确的是.
 满足
满足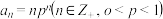 .对于说法:
.对于说法:①当
 时,数列
时,数列 为递减数列;
为递减数列;②当
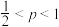 时,数列
时,数列 不一定有最大项;
不一定有最大项;③当
 时,数列
时,数列 为递减数列;
为递减数列;④当
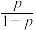 为正整数时,数列
为正整数时,数列 必有两项相等的最大项,
必有两项相等的最大项,正确的是.
| A.①② | B.③④ | C.②④ | D.②③ |
您最近一年使用:0次
2018-12-05更新
|
171次组卷
|
8卷引用:2013-2014学年湖北省襄阳市普通高中调研高一统一测试数学试卷
(已下线)2013-2014学年湖北省襄阳市普通高中调研高一统一测试数学试卷(已下线)2014届江西省宜春市高三考前模拟理科数学试卷2016届四川省成都市高三零模拟诊文科数学试卷(已下线)2014年全国高中数学联赛黑龙江赛区预赛试题(已下线)北京市西城区第四中学2019-2020学年高二上学期期中数学试题北京市陈经纶中学2020~2021学年度高二12月数学月考数学试题(已下线)4.1.1 数列的概念(练习)(已下线)第4章 数列 章末题型归纳总结(3)
9-10高二下·吉林·期中
名校
5 . 观察下列等式:
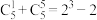 ,
,
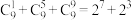 ,
,
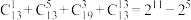 ,
,
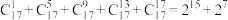 ,
,
……
由以上等式推测出一般的结论:对于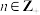 ,
,
______ .
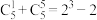 ,
,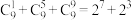 ,
,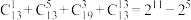 ,
,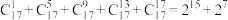 ,
,……
由以上等式推测出一般的结论:对于
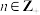 ,
,
您最近一年使用:0次
2018-12-04更新
|
143次组卷
|
9卷引用:2010年佛山一中高二下学期期末考试(理科)数学卷
(已下线)2010年佛山一中高二下学期期末考试(理科)数学卷(已下线)2010年河北省蔚县一中高二下学期期末考试数学卷(已下线)2010年吉林省东北师大附中高二下学期期中考试数学(理)(已下线)2011-2012学年江苏省无锡市第一中学高二下期中数学试卷(成志班)(已下线)2012-2013学年新课标高二下学期期中考试理科数学试卷(已下线)2012-2013学年江苏省沭阳县高二下学期期中调研测试理科数学试卷【校级联考】广东省深圳市耀华实验学校2017-2018学年高二下学期第二次月考数学(理)试题2016年全国高中数学联赛湖南赛区预赛试题沪教版(2020) 选修第二册 堂堂清 第6章 6.5(3)二项式定理(二项式定理及其应用)