1 . 将2024表示成5个正整数 ,
, ,
, ,
, ,
,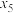 之和,得到方程
之和,得到方程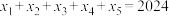 ①,称五元有序数组
①,称五元有序数组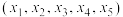 为方程①的解,对于上述的五元有序数组
为方程①的解,对于上述的五元有序数组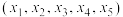 ,当
,当 时,若
时,若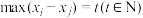 ,则称
,则称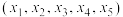 是
是 密集的一组解.
密集的一组解.
(1)方程①是否存在一组解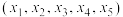 ,使得
,使得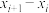
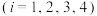 等于同一常数?若存在,请求出该常数;若不存在,请说明理由;
等于同一常数?若存在,请求出该常数;若不存在,请说明理由;
(2)方程①的解中共有多少组是 密集的?
密集的?
(3)记 ,问
,问 是否存在最小值?若存在,请求出
是否存在最小值?若存在,请求出 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
 ,
, ,
, ,
, ,
,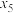 之和,得到方程
之和,得到方程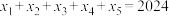 ①,称五元有序数组
①,称五元有序数组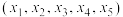 为方程①的解,对于上述的五元有序数组
为方程①的解,对于上述的五元有序数组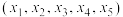 ,当
,当 时,若
时,若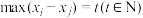 ,则称
,则称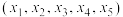 是
是 密集的一组解.
密集的一组解.(1)方程①是否存在一组解
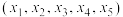 ,使得
,使得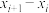
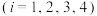 等于同一常数?若存在,请求出该常数;若不存在,请说明理由;
等于同一常数?若存在,请求出该常数;若不存在,请说明理由;(2)方程①的解中共有多少组是
 密集的?
密集的?(3)记
 ,问
,问 是否存在最小值?若存在,请求出
是否存在最小值?若存在,请求出 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
您最近一年使用:0次
2024-03-18更新
|
1191次组卷
|
2卷引用:广东省江门市2024届高三一模考试数学试卷
名校
解题方法
2 . 已知数列 的前
的前 项和为
项和为 ,且
,且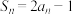 ,数列
,数列 满足
满足 ,记
,记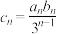 ,则下列说法正确的是( )
,则下列说法正确的是( )
 的前
的前 项和为
项和为 ,且
,且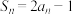 ,数列
,数列 满足
满足 ,记
,记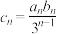 ,则下列说法正确的是( )
,则下列说法正确的是( )A.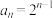 |
B. |
C.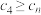 恒成立 恒成立 |
D.若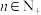 ,关于 ,关于 的不等式 的不等式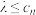 恰有两个解,则 恰有两个解,则 的取值范围为 的取值范围为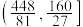 |
您最近一年使用:0次
2024-05-08更新
|
289次组卷
|
2卷引用:广东省顺德区北滘中学2023-2024学年高二下学期期中考试数学试卷
3 . 同余定理是数论中的重要内容.同余的定义为:设a,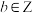 ,
, 且
且 .若
.若 则称a与b关于模m同余,记作
则称a与b关于模m同余,记作 (modm)(“|”为整除符号).
(modm)(“|”为整除符号).
(1)解同余方程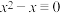 (mod3);
(mod3);
(2)设(1)中方程的所有正根构成数列 ,其中
,其中 .
.
①若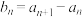 (
( ),数列
),数列 的前n项和为
的前n项和为 ,求
,求 ;
;
②若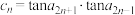 (
( ),求数列
),求数列 的前n项和
的前n项和 .
.
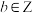 ,
, 且
且 .若
.若 则称a与b关于模m同余,记作
则称a与b关于模m同余,记作 (modm)(“|”为整除符号).
(modm)(“|”为整除符号).(1)解同余方程
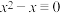 (mod3);
(mod3);(2)设(1)中方程的所有正根构成数列
 ,其中
,其中 .
.①若
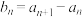 (
( ),数列
),数列 的前n项和为
的前n项和为 ,求
,求 ;
;②若
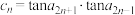 (
( ),求数列
),求数列 的前n项和
的前n项和 .
.
您最近一年使用:0次
2024-02-03更新
|
2808次组卷
|
9卷引用:黄金卷08(2024新题型)
(已下线)黄金卷08(2024新题型)广东省揭阳市普宁市华美实验学校2023-2024学年高二下学期第一次阶段考试数学试题安徽省合肥市第一中学2024届高三上学期期末质量检测数学试题湖北省武汉市华中师大第一附中2023-2024学年高二下学期数学独立作业(一)(已下线)压轴题函数与导数新定义题(九省联考第19题模式)练(已下线)新题型01 新高考新结构二十一大考点汇总-3重庆市万州二中教育集团2023-2024学年高二下学期入学质量监测数学试题(已下线)题型18 4类数列综合浙江省部分学校联考2024届高三高考适应性测试数学试题



