名校
1 . 已知函数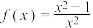 .
.
(1)用单调性的定义证明函数 在
在 上为增函数;
上为增函数;
(2)是否存在实数 ,使得当
,使得当 的定义域为
的定义域为 (
( ,
, )时,函数
)时,函数 的值域为
的值域为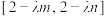 .若存在.求出
.若存在.求出 的取值范围;若不存在说明理由.
的取值范围;若不存在说明理由.
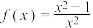 .
.(1)用单调性的定义证明函数
 在
在 上为增函数;
上为增函数;(2)是否存在实数
 ,使得当
,使得当 的定义域为
的定义域为 (
( ,
, )时,函数
)时,函数 的值域为
的值域为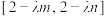 .若存在.求出
.若存在.求出 的取值范围;若不存在说明理由.
的取值范围;若不存在说明理由.
您最近一年使用:0次
7日内更新
|
747次组卷
|
2卷引用:河北省邢台市信都区邢台市第一中学2024-2025学年高一上学期第二次月考数学试题
2 . 已知函数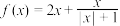 .
.
(1)判断函数 的奇偶性,并用定义证明;
的奇偶性,并用定义证明;
(2)判断函数 在
在 上的单调性,并用定义证明;
上的单调性,并用定义证明;
(3)若关于 的不等式
的不等式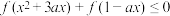 对任意实数
对任意实数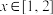 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
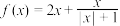 .
.(1)判断函数
 的奇偶性,并用定义证明;
的奇偶性,并用定义证明;(2)判断函数
 在
在 上的单调性,并用定义证明;
上的单调性,并用定义证明;(3)若关于
 的不等式
的不等式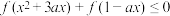 对任意实数
对任意实数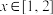 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
名校
解题方法
3 . 已知函数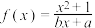 经过
经过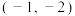 ,
,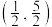 两点.
两点.
(1)求函数 的解析式;
的解析式;
(2)判断函数 在
在 上的单调性并用定义进行证明;
上的单调性并用定义进行证明;
(3)若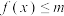 对任意
对任意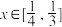 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
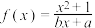 经过
经过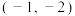 ,
,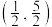 两点.
两点.(1)求函数
 的解析式;
的解析式;(2)判断函数
 在
在 上的单调性并用定义进行证明;
上的单调性并用定义进行证明;(3)若
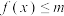 对任意
对任意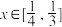 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
7日内更新
|
4069次组卷
|
11卷引用:河北省承德市双滦区实验中学2025届高三上学期10月月考数学试题
河北省承德市双滦区实验中学2025届高三上学期10月月考数学试题黑龙江省大庆铁人中学2024-2025学年高一上学期第一次月考数学试卷云南省红河哈尼族彝族自治州蒙自市红河哈尼族彝族自治州第一中学2024-2025学年高一上学期10月月考数学试题安徽省阜阳市第三中学2024-2025学年高一上学期10月月考数学试题山东省泰安市新泰市弘文中学2024-2025学年高一上学期10月月考数学试卷黑龙江省佳木斯市富锦市第一中学2024-2025学年高一上学期期中考试数学试卷江西省上饶市玉山文苑学校2024-2025学年高一上学期第二次检测数学试卷广东省佛山市南海区西樵高级中学2024-2025学年高一上学期第一次段考数学试卷新疆维吾尔自治区和田地区第二中学2024-2025学年高一上学期期中考试数学试题云南省红河哈尼族彝族自治州中央民族大学附属中学红河州实验学校2024-2025学年高一上学期中考试数学试题青海省西宁市第十四中学2024-2025学年高一上学期期中考试数学试卷
解题方法
4 . 已知函数 是定义在
是定义在 上的奇函数,当
上的奇函数,当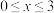 时,
时,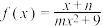 ,且
,且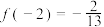 .
.
(1)求函数 的解析式;
的解析式;
(2)(i)判断函数 在
在 上的单调性,并用定义法证明;
上的单调性,并用定义法证明;
(ii)求不等式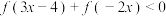 的解集.
的解集.
 是定义在
是定义在 上的奇函数,当
上的奇函数,当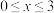 时,
时,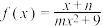 ,且
,且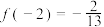 .
.(1)求函数
 的解析式;
的解析式;(2)(i)判断函数
 在
在 上的单调性,并用定义法证明;
上的单调性,并用定义法证明;(ii)求不等式
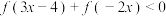 的解集.
的解集.
您最近一年使用:0次
解题方法
5 . 已知函数 的定义域为
的定义域为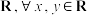 ,恒有
,恒有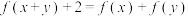 ,且当
,且当 时,
时,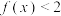 ,则下列结论正确的是( )
,则下列结论正确的是( )
 的定义域为
的定义域为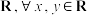 ,恒有
,恒有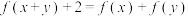 ,且当
,且当 时,
时,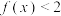 ,则下列结论正确的是( )
,则下列结论正确的是( )A.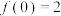 | B.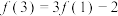 |
C.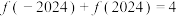 | D.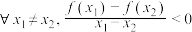 |
您最近一年使用:0次
解题方法
6 . 已知函数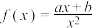 ,且
,且 ,
,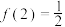 .
.
(1)求a和b的值;
(2)判断 在
在 上的单调性,并根据定义证明.
上的单调性,并根据定义证明.
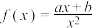 ,且
,且 ,
,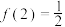 .
.(1)求a和b的值;
(2)判断
 在
在 上的单调性,并根据定义证明.
上的单调性,并根据定义证明.
您最近一年使用:0次
名校
解题方法
7 . 已知函数 的定义域为R,对任意实数
的定义域为R,对任意实数 满足
满足 .且
.且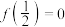 ,当
,当 时,
时,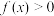 ,则下列结论正确的是( )
,则下列结论正确的是( )
 的定义域为R,对任意实数
的定义域为R,对任意实数 满足
满足 .且
.且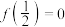 ,当
,当 时,
时,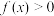 ,则下列结论正确的是( )
,则下列结论正确的是( )A.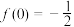 | B. | C. 为增函数 为增函数 | D. 为奇函数 为奇函数 |
您最近一年使用:0次
7日内更新
|
731次组卷
|
2卷引用:河北省石家庄一中实验学校2024-2025学年高三上学期第一次考试数学试题
8 . 已知 是定义域为
是定义域为 的偶函数,且当
的偶函数,且当 时,
时, 是增函数.若
是增函数.若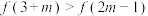 ,则m的取值范围为( )
,则m的取值范围为( )
 是定义域为
是定义域为 的偶函数,且当
的偶函数,且当 时,
时, 是增函数.若
是增函数.若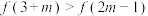 ,则m的取值范围为( )
,则m的取值范围为( )A.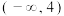 | B.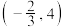 |
C. | D.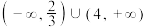 |
您最近一年使用:0次
解题方法
9 . 已知函数 为定义在R上的奇函数,且在
为定义在R上的奇函数,且在 上单调递减,满足
上单调递减,满足 ,则实数a的取值范围为( )
,则实数a的取值范围为( )
 为定义在R上的奇函数,且在
为定义在R上的奇函数,且在 上单调递减,满足
上单调递减,满足 ,则实数a的取值范围为( )
,则实数a的取值范围为( )A.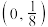 | B.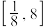 | C.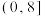 | D. |
您最近一年使用:0次
名校
解题方法
10 . 已知幂函数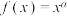 图象经过点
图象经过点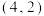 ,若
,若 ,则实数
,则实数 的取值范围是
的取值范围是______ ;若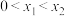 ,则
,则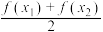
______ 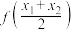
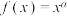 图象经过点
图象经过点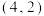 ,若
,若 ,则实数
,则实数 的取值范围是
的取值范围是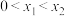 ,则
,则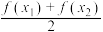
您最近一年使用:0次



