名校
1 . 若函数 是定义域内的增函数,且函数
是定义域内的增函数,且函数 在区间
在区间 上单调递减,则实数
上单调递减,则实数 的取值范围是
的取值范围是_____
 是定义域内的增函数,且函数
是定义域内的增函数,且函数 在区间
在区间 上单调递减,则实数
上单调递减,则实数 的取值范围是
的取值范围是
您最近一年使用:0次
2024-10-16更新
|
88次组卷
|
2卷引用:湖南省株洲市炎陵县2024-2025学年高二上学期10月份综合素质检测数学试题
2024高三·全国·专题练习
解题方法
2 . 已知函数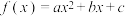 的图象如图所示,则下列结论错误的是( )
的图象如图所示,则下列结论错误的是( )
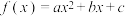 的图象如图所示,则下列结论错误的是( )
的图象如图所示,则下列结论错误的是( )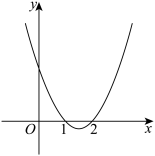
A. |
B. |
C. |
D.不等式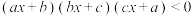 的解集是 的解集是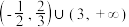 |
您最近一年使用:0次
2024-08-01更新
|
1067次组卷
|
4卷引用:湖南省邵阳市海谊中学2024-2025学年高二上学期分班(入学)考试数学试题
湖南省邵阳市海谊中学2024-2025学年高二上学期分班(入学)考试数学试题湖南省衡阳市衡阳县第四中学2024-2025学年高一上学期9月月考数学试题(已下线)周测2 一元二次函数、方程和不等式【北京专版】(已下线)2.4 二次函数【讲】(北京专版高三一轮)
名校
解题方法
3 . 已知函数 是定义在
是定义在 上的偶函数;且在
上的偶函数;且在 上单调递增,若对于任意的
上单调递增,若对于任意的 ,不等式
,不等式 恒成立,则
恒成立,则 的取值范围是( )
的取值范围是( )
 是定义在
是定义在 上的偶函数;且在
上的偶函数;且在 上单调递增,若对于任意的
上单调递增,若对于任意的 ,不等式
,不等式 恒成立,则
恒成立,则 的取值范围是( )
的取值范围是( )A. | B.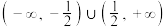 | C.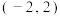 | D.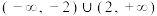 |
您最近一年使用:0次
2024-07-05更新
|
1055次组卷
|
2卷引用:湖南省长沙市长郡中学2024-2025学年高二上学期入学考试数学试题
名校
解题方法
4 . 若函数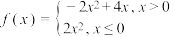 在区间
在区间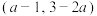 上有最大值,则实数a的取值范围是
上有最大值,则实数a的取值范围是_________ .
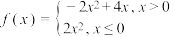 在区间
在区间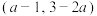 上有最大值,则实数a的取值范围是
上有最大值,则实数a的取值范围是
您最近一年使用:0次
2024-03-24更新
|
1674次组卷
|
8卷引用:湖南省永州市第一中学2023-2024学年高二下学期6月月考数学试题
湖南省永州市第一中学2023-2024学年高二下学期6月月考数学试题北京市第二十中学2023-2024学年高一下学期开学模拟考试数学试题(已下线)第03讲 幂函数与二次函数(八大题型)(讲义)(已下线)专题拓展:分段函数常见考法-【暑假自学课】-(人教A版2019必修第一册)(已下线)热点专题 2-3 幂函数与二次函数,方程与不等式【12类题型】(已下线)二次函数与幂函数01-一轮复习考点专练(已下线)2.4 二次函数(高三一轮)【讲】 (提升版)上海市实验学校2025届高三上学期9月月考数学试卷
5 . 已知二次函数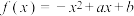 的图象关于直线
的图象关于直线 对称,且最大值为4.
对称,且最大值为4.
(1)求函数 的解析式;
的解析式;
(2)设 ,试比较
,试比较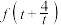 与
与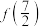 的大小;
的大小;
(3)若实数 满足:①函数
满足:①函数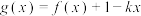 有两个不同的零点;②方程
有两个不同的零点;②方程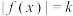 有四个不同的实数根,求
有四个不同的实数根,求 的取值范围.
的取值范围.
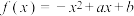 的图象关于直线
的图象关于直线 对称,且最大值为4.
对称,且最大值为4.(1)求函数
 的解析式;
的解析式;(2)设
 ,试比较
,试比较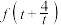 与
与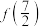 的大小;
的大小;(3)若实数
 满足:①函数
满足:①函数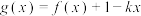 有两个不同的零点;②方程
有两个不同的零点;②方程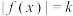 有四个不同的实数根,求
有四个不同的实数根,求 的取值范围.
的取值范围.
您最近一年使用:0次
名校
6 . 函数 和
和 的图象关于原点对称,且
的图象关于原点对称,且 .
.
(1)求函数 的解析式;
的解析式;
(2)解不等式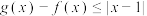 ;
;
(3)若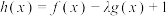 在
在 上是增函数,求实数
上是增函数,求实数 的取值范围.
的取值范围.
 和
和 的图象关于原点对称,且
的图象关于原点对称,且 .
.(1)求函数
 的解析式;
的解析式;(2)解不等式
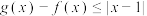 ;
;(3)若
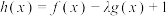 在
在 上是增函数,求实数
上是增函数,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2023-11-17更新
|
240次组卷
|
2卷引用:湖南省名校联合体2023-2024学年高二上学期期中数学试题
名校
解题方法
7 . 已知函数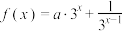 是定义域为
是定义域为 的偶函数.
的偶函数.
(1)求a的值;
(2)若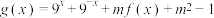 ,求函数
,求函数 的最小值.
的最小值.
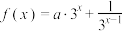 是定义域为
是定义域为 的偶函数.
的偶函数.(1)求a的值;
(2)若
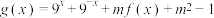 ,求函数
,求函数 的最小值.
的最小值.
您最近一年使用:0次
2023-10-16更新
|
2118次组卷
|
7卷引用:湖南省长沙市南雅中学2023-2024学年高二下学期第二次月考(5月)数学试题
湖南省长沙市南雅中学2023-2024学年高二下学期第二次月考(5月)数学试题安徽省合肥市第一中学2024届高三上学期第一次教学质量检测(10月)数学试题辽宁省大连市第八中学2023-2024学年高一上学期期中数学试题(已下线)第01讲 4.1指数+4.2指数函数—【练透核心考点】(已下线)热点2-2 函数的最值(值域)及应用(8题型+满分技巧+限时检测)(已下线)考点9 与二次函数相关的参数问题 --2024届高考数学考点总动员【讲】陕西省渭南市蒲城县桥山中学2024-2025学年高三上学期第一次月考数学试题
名校
解题方法
8 . 设函数 是定义域为
是定义域为 的偶函数,
的偶函数, 是定义域为
是定义域为 的奇函数,且
的奇函数,且
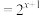 .
.
(1)求 与
与 的解析式;
的解析式;
(2)若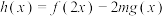 在
在 上的最小值为
上的最小值为 ,求
,求 的值.
的值.
 是定义域为
是定义域为 的偶函数,
的偶函数, 是定义域为
是定义域为 的奇函数,且
的奇函数,且
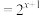 .
.(1)求
 与
与 的解析式;
的解析式;(2)若
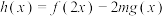 在
在 上的最小值为
上的最小值为 ,求
,求 的值.
的值.
您最近一年使用:0次
2023-02-11更新
|
1282次组卷
|
11卷引用:湖南省长沙市雅礼中学2022-2023学年高二下学期5月月考数学试题
湖南省长沙市雅礼中学2022-2023学年高二下学期5月月考数学试题湖南省长沙市长郡湘府中学2022-2023学年高二下学期期末模拟数学试题广东省汕尾市普宁华美实验学校2024-2025学年高二上学期10月月考数学试题广东省茂名市五校联盟2022-2023学年高一上学期期末联考数学试题第三章 指数运算与指数函数 单元检测-2022-2023学年高一上学期数学北师大版(2019)必修第一册黑龙江省哈尔滨市第六中学校2022-2023学年高一上学期期末适应性训练数学试题黑龙江省佳木斯市第一中学2023-2024学年高三上学期第二次调研考试数学试题(已下线)高一数学第一学期期末押题密卷06卷-《考点·题型·难点》期末高效复习广东省汕头市潮阳第一中学2023-2024学年高一下学期入学学情摸查限时训练数学试题黑龙江省大庆市林甸县第一中学2023-2024学年高一下学期期初考试数学试题(已下线)第04讲 指数与指数函数(八大题型)(练习)
名校
解题方法
9 . 已知函数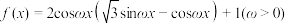 ,
, 的最小正周期为
的最小正周期为 .
.
(1)求 单调递增区间;
单调递增区间;
(2)是否存在实数m满足对任意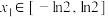 ,任意
,任意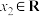 ,使
,使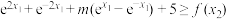 成立.若存在,求m的取值范围;若不存在,说明理由.
成立.若存在,求m的取值范围;若不存在,说明理由.
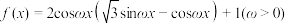 ,
, 的最小正周期为
的最小正周期为 .
.(1)求
 单调递增区间;
单调递增区间;(2)是否存在实数m满足对任意
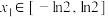 ,任意
,任意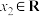 ,使
,使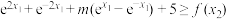 成立.若存在,求m的取值范围;若不存在,说明理由.
成立.若存在,求m的取值范围;若不存在,说明理由.
您最近一年使用:0次
2022-07-03更新
|
939次组卷
|
3卷引用:湖南省邵阳市第二中学2022-2023学年高二上学期入学考试数学试题
名校
10 . 已知函数 .
.
(1)若函数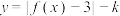 在
在 上有且仅有一个零点,求实数k的取值范围;
上有且仅有一个零点,求实数k的取值范围;
(2)是否存在实数m,使得函数 在[a,b]上的值域为[2a,2b],若存在,求出实数m的取值范围;若不存在,说明理由.
在[a,b]上的值域为[2a,2b],若存在,求出实数m的取值范围;若不存在,说明理由.
 .
.(1)若函数
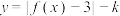 在
在 上有且仅有一个零点,求实数k的取值范围;
上有且仅有一个零点,求实数k的取值范围;(2)是否存在实数m,使得函数
 在[a,b]上的值域为[2a,2b],若存在,求出实数m的取值范围;若不存在,说明理由.
在[a,b]上的值域为[2a,2b],若存在,求出实数m的取值范围;若不存在,说明理由.
您最近一年使用:0次
2022-02-22更新
|
519次组卷
|
3卷引用:湖南省长沙市四校联考2022-2023学年高二上学期9月阶段考试数学试题



