名校
解题方法
1 . 在 中,
中,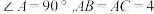 ,点
,点 为边
为边 的中点,点
的中点,点 在边
在边 上,则
上,则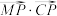 的最小值为
的最小值为________ .
 中,
中,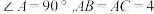 ,点
,点 为边
为边 的中点,点
的中点,点 在边
在边 上,则
上,则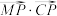 的最小值为
的最小值为
您最近一年使用:0次
2023-03-11更新
|
1259次组卷
|
6卷引用:福建省福州市八县(市、区)一中2023届高三上学期期中联考数学试题
福建省福州市八县(市、区)一中2023届高三上学期期中联考数学试题(已下线)第74练 计算提升训练142023年2月安徽省普通高中学业水平考试数学模拟试题(三)广东省佛山市荣山中学2022-2023学年高一下学期期中数学试题(已下线)高一下册数学期中模拟卷(二)江西省南昌市新民外语学校2023-2024学年高一下学期期中考试数学试题
解题方法
2 . 下列结论中,正确的结论有( )
A.若 , , ,则 ,则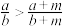 |
B.如果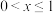 ,那么 ,那么 取得最大值时x的值为1 取得最大值时x的值为1 |
C.已知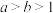 ,则 ,则 |
D.若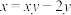 , , , ,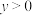 ,则 ,则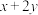 的最小值是8 的最小值是8 |
您最近一年使用:0次
名校
3 . 已知函数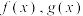 分别为定义在
分别为定义在 上的奇函数和偶函数,且满足
上的奇函数和偶函数,且满足 .若函数
.若函数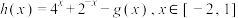 ,则
,则 的值域为
的值域为__________ .
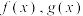 分别为定义在
分别为定义在 上的奇函数和偶函数,且满足
上的奇函数和偶函数,且满足 .若函数
.若函数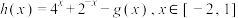 ,则
,则 的值域为
的值域为
您最近一年使用:0次
2022-11-26更新
|
881次组卷
|
2卷引用:福建师范大学附属中学2023届高三上学期12月月考数学试题
名校
解题方法
4 . 已知正实数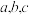 满足
满足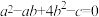 ,当
,当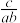 取最小值时,下列说法正确的是( )
取最小值时,下列说法正确的是( )
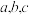 满足
满足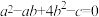 ,当
,当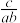 取最小值时,下列说法正确的是( )
取最小值时,下列说法正确的是( )A.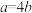 | B.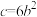 |
C.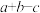 的最大值为 的最大值为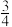 | D.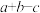 的最大值为 的最大值为 |
您最近一年使用:0次
2022-10-21更新
|
229次组卷
|
2卷引用:福建省福州市三校2023届高三上学期期中联考数学试题
名校
解题方法
5 . 第四届中国国际进口博览会于2021年11月5日至10日在上海举行.本届进博会有4000多项新产品、新技术、新服务.某跨国公司带来了高端空调模型参展,通过展会调研,中国甲企业计划在2022年与该跨国公司合资生产此款空调.生产此款空调预计全年需投入固定成本260万元,生产x千台空调,需另投入资金R万元,且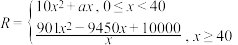 .经测算,当生产10千台空调时需另投入的资金R=4000万元.现每台空调售价为0.9万元时,当年内生产的空调当年能全部销售完.
.经测算,当生产10千台空调时需另投入的资金R=4000万元.现每台空调售价为0.9万元时,当年内生产的空调当年能全部销售完.
(1)求2022年该企业年利润W(万元)关于年产量x(千台)的函数关系式;
(2)2022年产量为多少时,该企业所获年利润最大?最大年利润为多少?注:利润=销售额-成本.
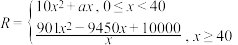 .经测算,当生产10千台空调时需另投入的资金R=4000万元.现每台空调售价为0.9万元时,当年内生产的空调当年能全部销售完.
.经测算,当生产10千台空调时需另投入的资金R=4000万元.现每台空调售价为0.9万元时,当年内生产的空调当年能全部销售完.(1)求2022年该企业年利润W(万元)关于年产量x(千台)的函数关系式;
(2)2022年产量为多少时,该企业所获年利润最大?最大年利润为多少?注:利润=销售额-成本.
您最近一年使用:0次
2022-08-09更新
|
4072次组卷
|
46卷引用:福建省龙岩第一中学2023届高三上学期第一次月考数学试题
福建省龙岩第一中学2023届高三上学期第一次月考数学试题北师大版(2019) 必修第一册 名校名师卷 高考水平模拟性测试河北省邢台市第二中学2023届高三上学期第一次月考数学试题北京师范大学第二附属中学2023届高三上学期10月月考数学试题宁夏银川市第二中学2023届高三上学期统练三数学(理)试题宁夏回族自治区银川市第六中学2022-2023学年高三上学期11月月考数学试题宁夏育才中学2023届高三上学期月考(三)数学(理)试题福建省政和县第一中学2024届高三上学期第一次月考数学试题福建省连城县第一中学2020-2021学年高一上学期第二次月考数学试题福建省三明第一中学2021-2022学年高一上学期第二次月考数学试题广东省深圳市深圳高级中学2021-2022学年高一上学期期末数学试题(已下线)2023届高三第一次月考押题卷(测试范围:集合与常用逻辑用语、不等式、函数与导数)2023版 湘教版(2019) 必修第一册 名师精选卷 高考水平模拟性测试(已下线)突破3.4 函数的应用(一)(重难点突破)湖北省武汉市2022-2023学年高一上学期期中模拟数学试题广东省广州市真光中学2022-2023学年高一上学期10月月考数学试题宁夏回族自治区银川一中2022-2023学年高一上学期期中考试数学试题广东省深圳市福田外国语高级中学2022-2023学年高一上学期期中数学试题湖南省湘东名校(茶陵一中、攸县一中、株洲市二中、醴陵二中)2022-2023学年高一上学期期中联考数学试题宁夏银川市兴庆区2022-2023学年高一上学期期中联考数学试题山东省济宁市微山县第二中学2022-2023学年高一上学期期中数学试题山东省济宁市兖州区2022-2023学年高一上学期期中考试数学试题四川省宜宾市第四中学校2022-2023学年高一上学期期中考试数学试题河南省周口市郸城县第一高级中学2022-2023学年高一上学期第一次月考数学试题湖北省武汉市水果湖高级中学2022-2023学年高一上学期10月线上月考数学试题河南省南阳市第一中学校2022-2023学年高一上学期12月月考数学试题河南省周口市太康县第三高级中学2022-2023学年高一上学期12月月考数学试题(已下线)专题3.4 函数的应用(一)(3类必考点)-2022-2023学年高一数学必考点分类集训系列(人教A版2019必修第一册)浙江省杭州学军中学海创园2022-2023学年高一上学期期中数学试题(已下线)专题3.7 函数的应用(一)-重难点题型精讲-2022-2023学年高一数学举一反三系列(人教A版2019必修第一册)第4章 指数概念与对数函数(基础、典型、易错、新文化、压轴)专项训练山东省枣庄市第八中学2024届高三上学期10月月考数学试题辽宁省大连长兴岛高级中学2023-2024学年高三上学期第一次月考数学试题吉林省梅河口市第五中学2023-2024学年高三上学期期中数学试题山东省潍坊市2019-2020学年高一上学期期中数学试题湖南省怀化市2020-2021学年高二上学期期末数学试题海南省海口市海口中学2021-2022学年高一上学期期中考试数学试题山东省青岛市青岛第五十八中学2020-2021学年高一上学期期中数学试题湖南省湘潭市湘潭县第一中学2022-2023学年高一上学期期末数学试题山东省新泰市第一中学东校2022-2023学年高二下学期第二次质量检测数学试题湖南省株洲市炎陵县2022-2023学年高一下学期开学考试数学试题(已下线)3.4函数的应用(一)(分层作业)-【上好课】湖北省宜昌市部分省级示范高中2023-2024学年高一上学期9月考试数学试题湖北省宜昌市宜都市第二中学2023-2024学年高一上学期10月月考数学试题湖南省郴州市桂阳县甘甜中学2023-2024学年高一上学期第一次月考数学试题河南省济源市高级中学2023-2024学年高一上学期11月月考数学试题
名校
6 . 若命题“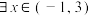 ,
, ”为真命题,则实数
”为真命题,则实数 可取的最小整数值是( )
可取的最小整数值是( )
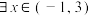 ,
, ”为真命题,则实数
”为真命题,则实数 可取的最小整数值是( )
可取的最小整数值是( )A. | B.0 | C.1 | D.3 |
您最近一年使用:0次
2022-05-10更新
|
2455次组卷
|
10卷引用:福建省莆田华侨中学2022届高三考前最后一卷数学试题
福建省莆田华侨中学2022届高三考前最后一卷数学试题陕西省西安市周至县2022届高三下学期三模文科数学试题河南省睢县高级中学2022-2023学年高三上学期9月考试数学(理科)试题(已下线)第02讲 常用逻辑用语 (精讲+精练)-2(已下线)专题02 常用逻辑用语-2023届高考数学一轮复习精讲精练(新高考专用)(已下线)突破1.5全称量词与存在量词(课时训练)湖南省衡阳市祁东县育贤中学2022-2023学年高一上学期第一次月考数学试题陕西省咸阳中学2022-2023学年高二上学期期中理科数学试题(已下线)专题04 常用逻辑用语-2(已下线)周测1 集合与常用逻辑用语 一轮周测卷(基础卷)
7 . 已知函数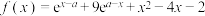 有零点,则实数
有零点,则实数
___________ .
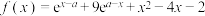 有零点,则实数
有零点,则实数
您最近一年使用:0次
名校
解题方法
8 . 一个车间为了规定工时定额,需要确定一台机器持续加工零件所花费的时间,为此进行了10次试验,收集数据如表所示:
(1)通过数据分析,发现y与x之间呈线性相关关系,求y关于x的回归方程,并预测持续加工480个零件所花费的时间;
(2)机器持续工作,高负荷运转,会影响产品质量.经调查,机器持续工作前6小时内所加工出来的零件的次品率为0.1,之后加工出来的零件的次品率为0.2.(机器持续运行时间不超过12小时)已知每个正品零件售价100元,次品零件作废,持续加工x个零件的生产成本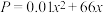 (单位:元).根据(1)的回归方程,估计一台机器持续工作多少分钟所获利润最大?(利润=零件正品数
(单位:元).根据(1)的回归方程,估计一台机器持续工作多少分钟所获利润最大?(利润=零件正品数 售价-生产成本)
售价-生产成本)
参考数据: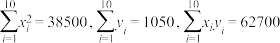
附:对于一组数据(x1,y1),(x2,y2),·,(xn,yn),其回归直线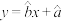 a的斜率和截距的最小二乘估计分别为
a的斜率和截距的最小二乘估计分别为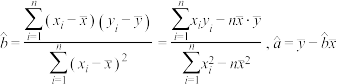
| 零件数x/个 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| 时间y/分钟 | 76 | 85 | 92 | 95 | 100 | 110 | 115 | 121 | 125 | 131 |
(2)机器持续工作,高负荷运转,会影响产品质量.经调查,机器持续工作前6小时内所加工出来的零件的次品率为0.1,之后加工出来的零件的次品率为0.2.(机器持续运行时间不超过12小时)已知每个正品零件售价100元,次品零件作废,持续加工x个零件的生产成本
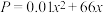 (单位:元).根据(1)的回归方程,估计一台机器持续工作多少分钟所获利润最大?(利润=零件正品数
(单位:元).根据(1)的回归方程,估计一台机器持续工作多少分钟所获利润最大?(利润=零件正品数 售价-生产成本)
售价-生产成本)参考数据:
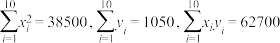
附:对于一组数据(x1,y1),(x2,y2),·,(xn,yn),其回归直线
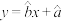 a的斜率和截距的最小二乘估计分别为
a的斜率和截距的最小二乘估计分别为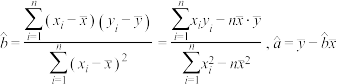
您最近一年使用:0次
2022-03-11更新
|
715次组卷
|
3卷引用:福建省厦门市2022届高三毕业班3月第二次质量检测数学试题
名校
9 . 2020年11月5日至10日,第三届中国国际进口博览会在上海举行,经过三年发展,进博会让展品变商品,让展商变投资商,交流创意和理念,联通中国和世界,国际采购、投资促进、人文交流,开放合作四大平台作用不断凸显,成为全球共享的国际公共产品.在消费品展区,某企业带来了一款新型节能环保产品参展,并决定大量投放市场.已知该产品年固定研发成本为150万元,每生产1万台需另投入380万元.设该企业一年内生产该产品 万台且全部售完,每万台的销售收入为
万台且全部售完,每万台的销售收入为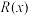 万元,且
万元,且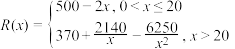 .
.
(1)写出年利润 (万元)关于年产量
(万元)关于年产量 (万台)的函数解析式;(利润 = 销售收入—成本)
(万台)的函数解析式;(利润 = 销售收入—成本)
(2)当年产量为多少万台时,该企业获得的年利润最大?并求出最大年利润.
 万台且全部售完,每万台的销售收入为
万台且全部售完,每万台的销售收入为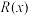 万元,且
万元,且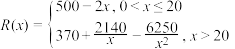 .
.(1)写出年利润
 (万元)关于年产量
(万元)关于年产量 (万台)的函数解析式;(利润 = 销售收入—成本)
(万台)的函数解析式;(利润 = 销售收入—成本)(2)当年产量为多少万台时,该企业获得的年利润最大?并求出最大年利润.
您最近一年使用:0次
2021-11-11更新
|
1385次组卷
|
14卷引用:福建省上杭县第五中学2023届高三上学期8月月考数学试题
福建省上杭县第五中学2023届高三上学期8月月考数学试题上海市交通大学附属中学2022届高三下学期开学考数学试题山东省济南外国语学校2021-2022学年高三上学期11月月考数学试题上海市2023届高三下学期开学摸底数学试题湖南省彬州市安仁县第一中学2022-2023学年高一上学期第七次月考数学试题(已下线)专题13 函数模型及其应用-1山东省泰安市泰安第二中学2023-2024学年高三上学期10月月考数学试题山东省济南市2020-2021学年高一上学期期末数学试题北京市清华大学附属中学朝阳学校2021~2022学年高一上学期期中考试数学试题湖北省襄阳市第五中学2021-2022学年高一上学期期中数学试题山东省泰安市宁阳县复圣中学2022-2023学年高一上学期期末数学试题广东省佛山市顺德区乐从中学2023-2024学年高一上学期第一次质量检测数学试题广东省肇庆市封开县广信中学2023-2024学年高一上学期期中数学试题北京市海淀区宏志中学2023-2024学年高一上学期期中考试数学试卷
名校
解题方法
10 . 已知函数 ,
, .
.
(1)判断 的奇偶性和单调性;
的奇偶性和单调性;
(2)若对任意 ,存在
,存在 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
 ,
, .
.(1)判断
 的奇偶性和单调性;
的奇偶性和单调性;(2)若对任意
 ,存在
,存在 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2021-10-12更新
|
1136次组卷
|
8卷引用:福建省厦门外国语学校2023届高三上学期10月月考数学试题
福建省厦门外国语学校2023届高三上学期10月月考数学试题福建省仙游县枫亭中学2023届高三上学期期中考试数学试题河南中原名校2021-2022学年上学期高三第一次联考文科数学试题河南省豫南九校联盟2021-2022学年高三上学期第一次联考数学(文)试题陕西省榆林市第十中学2021-2022学年高二下学期期中文科数学试题(已下线)专题4.2 对数及对数函数-《聚能闯关》2021-2022学年高一数学提优闯关训练(人教A版2019必修第一册)(已下线)专题4.4 对数函数-《讲亮点》2021-2022学年高一数学新教材同步配套讲练(人教A版2019必修第一册)湖南省湘西州2021-2022学年高一上学期期末数学试题



