名校
解题方法
1 . “费马点”是由十七世纪法国数学家费马提出并征解的一个问题.该问题是:“在一个三角形内求作一点,使其与此三角形的三个顶点的距离之和最小.”意大利数学家托里拆利给出了解答,当 的三个内角均小于
的三个内角均小于 时,使得
时,使得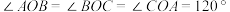 的点
的点 即为费马点;当
即为费马点;当 有一个内角大于或等于
有一个内角大于或等于 时,最大内角的顶点为费马点.试用以上知识解决下面问题:已知
时,最大内角的顶点为费马点.试用以上知识解决下面问题:已知 的内角
的内角 所对的边分别为
所对的边分别为 ,且
,且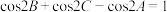
(1)求 ;
;
(2)若 ,设点
,设点 为
为 的费马点,求
的费马点,求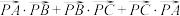 ;
;
(3)设点 为
为 的费马点,
的费马点,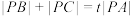 ,求实数
,求实数 的最小值.
的最小值.
 的三个内角均小于
的三个内角均小于 时,使得
时,使得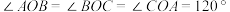 的点
的点 即为费马点;当
即为费马点;当 有一个内角大于或等于
有一个内角大于或等于 时,最大内角的顶点为费马点.试用以上知识解决下面问题:已知
时,最大内角的顶点为费马点.试用以上知识解决下面问题:已知 的内角
的内角 所对的边分别为
所对的边分别为 ,且
,且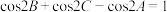
(1)求
 ;
;(2)若
 ,设点
,设点 为
为 的费马点,求
的费马点,求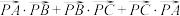 ;
;(3)设点
 为
为 的费马点,
的费马点,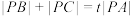 ,求实数
,求实数 的最小值.
的最小值.
您最近一年使用:0次
2024-03-03更新
|
4380次组卷
|
37卷引用:云南省昆明市五华区云南师范大学附属中学2023-2024学年高一下学期3月月考数学试题
云南省昆明市五华区云南师范大学附属中学2023-2024学年高一下学期3月月考数学试题重庆市求精中学校2023-2024学年高二下学期阶段测试数学试题2024届高三新高考改革数学适应性练习(7)(九省联考题型)(已下线)第六章 本章综合--方法提升应用【第三练】“上好三节课,做好三套题“高中数学素养晋级之路河北省沧州市泊头市第一中学2023-2024学年高一下学期3月月考数学试题湖南省长沙市明德中学2023-2024学年高一下学期3月月考数学试题山东省实验中学2023-2024学年高一下学期第一次阶段测试(3月)数学试题海南省海口市海南中学2023-2024学年高一下学期3月月考数学试题(已下线)模块五 专题四 全真能力模拟2(高一期中模拟)重庆市乌江新高考协作体2023-2024学年高一下学期第一阶段学业质量联合调研抽测(4月)数学试题河北省衡水市郑口中学2023-2024学年高一下学期质检一数学试题广东省中山市桂山中学2023-2024学年高一下学期第一次段考检测数学试题甘肃省张掖中学2023-2024学年高一下学期4月月考数学试卷四川省射洪中学校2023-2024学年高一强基班下学期第一次学月考试(4月)数学试题河南省郑州市基石中学2023-2024学年高一下学期4月月考数学试题广东省东莞市东莞中学松山湖学校2023-2024学年高一下学期第一次段考数学试题安徽省皖北名校2023-2024学年高一下学期阶段性联考数学试卷广东省深圳外国语学校2023-2024学年高一下学期4月月考数学试卷吉林省长春市十一高中2023-2024学年高一下学期4月月考数学试题湖北省武汉市第六中学2023-2024学年高一下学期4月月考数学试卷广东省江门市第一中学2023-2024学年高一下学期第一次阶段考试数学试题湖南省慈利县第一中学2023-2024学年高一下学期期中考试数学试题单元测试A卷——第六章?平面向量及其应用上海市第二中学2023-2024学年高一下学期期中考试数学试卷四川省南充市嘉陵第一中学2023-2024学年高一下学期4月期中考试数学试题山东省淄博市高青县第一中学2023-2024学年高一下学期期中考试数学试题福建省浦城第一中学2023-2024学年高一下学期4月期中考试数学试题上海市宜川中学2023-2024学年高一下学期期中考试数学试题江苏省南京市中华中学2023-2024学年高一下学期期中联考数学试题福建省厦门市湖滨中学2023-2024学年高一下学期期中考试数学试题广东省广州市白云艺术中学2023-2024学年高一下学期期中数学试题广东省广州市第六十五中学2023-2024学年高一下学期期中考试数学试卷重庆市涪陵第五中学校2023-2024学年高一下学期第一次月考数学试题山东省青岛市第五十八中学2023-2024学年高一下学期期中考试数学试题福建省莆田第八中学2023-2024学年高一下学期期中考试数学试卷辽宁省沈阳市五校协作体2023-2024学年高一下学期5月期中考试数学试题山东省聊城一中2023-2024学年下学期期中考试高一数学试题
名校
2 . “不以规矩,不能成方圆”,出自《孟子·离娄章句上》.“规”指圆规,“矩”指由相互垂直的长短两条直尺构成的角尺,是用来测量、画圆和方形图案的工具。有一块圆形木板,以“矩”量之,较长边为10cm,较短边为5cm,如图所示,将这块圆形木板截出一块三角形木块,三角形顶点 都在圆周上,角
都在圆周上,角 的对边分别为
的对边分别为 ,
, ,
, ,满足
,满足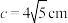

(1)求
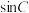 ;
;(2)若
 的面积为
的面积为 ,且
,且 ,求
,求 的周长
的周长
您最近一年使用:0次
2023-03-14更新
|
1582次组卷
|
8卷引用:云南省昆明市2023届“三诊一模”高三复习教学质量检测数学
云南省昆明市2023届“三诊一模”高三复习教学质量检测数学(已下线)专题19新文化与创新试题(已下线)专题07三角函数与解三角形(解答题)广西河池市八校2022-2023学年高一下学期第一次联考(4月)数学试题江苏省南京师范大学附属实验学校2022-2023学年高一下学期期中数学试题河北省衡水市第二中学2022-2023学年高一下学期期中数学试题(已下线)考点16 解三角形实际应用问题 --2024届高考数学考点总动员【练】山东省菏泽市第一中学八一路校区2023-2024学年高一下学期3月月考数学试题
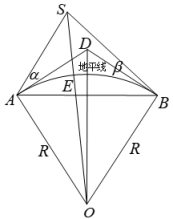
3 . 仰望星空,时有流星划过天际,令我们感叹生命的短暂,又深深震撼我们凡俗的心灵.流星是什么?从古至今,人们作过无数种猜测.古希腊亚里士多德说,那是地球上的蒸发物,近代有人进一步认为,那是地球上磷火升空后的燃烧现象.10世纪波斯著名数学家、天文学家阿尔·库希设计出一种方案,通过两个观测者异地同时观察同一颗流星,来测定其发射点的高度.如图,假设地球是一个标准的球体, 为地球的球心,
为地球的球心, 为地平线,有两个观测者在地球上的
为地平线,有两个观测者在地球上的 ,
, 两地同时观测到一颗流星
两地同时观测到一颗流星 ,观测的仰角分别为
,观测的仰角分别为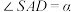 ,
,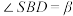 ,其中,
,其中,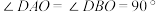 ,为了方便计算,我们考虑一种理想状态,假设两个观测者在地球上的
,为了方便计算,我们考虑一种理想状态,假设两个观测者在地球上的 ,
, 两点测得
两点测得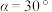 ,
,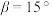 ,地球半径为
,地球半径为 公里,两个观测者的距离
公里,两个观测者的距离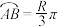 .(参考数据:
.(参考数据: ,
,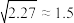 )
)
(1)求流星 发射点近似高度
发射点近似高度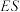 ;
;
(2)在古希腊,科学不发达,人们看到流星以为这是地球水分蒸发后凝结的固体,已知对流层高度大约在18公里左右,若地球半径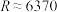 公里,请你据此判断该流星
公里,请你据此判断该流星 是地球蒸发物还是“天外来客”?并说明理由.
是地球蒸发物还是“天外来客”?并说明理由.
 为地球的球心,
为地球的球心, 为地平线,有两个观测者在地球上的
为地平线,有两个观测者在地球上的 ,
, 两地同时观测到一颗流星
两地同时观测到一颗流星 ,观测的仰角分别为
,观测的仰角分别为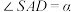 ,
,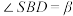 ,其中,
,其中,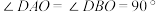 ,为了方便计算,我们考虑一种理想状态,假设两个观测者在地球上的
,为了方便计算,我们考虑一种理想状态,假设两个观测者在地球上的 ,
, 两点测得
两点测得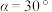 ,
,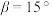 ,地球半径为
,地球半径为 公里,两个观测者的距离
公里,两个观测者的距离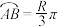 .(参考数据:
.(参考数据: ,
,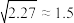 )
)
(1)求流星
 发射点近似高度
发射点近似高度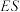 ;
;(2)在古希腊,科学不发达,人们看到流星以为这是地球水分蒸发后凝结的固体,已知对流层高度大约在18公里左右,若地球半径
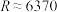 公里,请你据此判断该流星
公里,请你据此判断该流星 是地球蒸发物还是“天外来客”?并说明理由.
是地球蒸发物还是“天外来客”?并说明理由.
您最近一年使用:0次
2021-07-14更新
|
1119次组卷
|
5卷引用:云南师范大学附属中学2020-2021学年高一下学期期中考试数学试题
云南师范大学附属中学2020-2021学年高一下学期期中考试数学试题(已下线)数学与地理(已下线)6.4平面向量的应用B卷(已下线)第6章 平面向量及其应用(新文化30题专练)-2021-2022学年高一数学考试满分全攻略(人教A版2019必修第二册)广东省广州市三校联考2021-2022学年高一下学期期中数学试题
名校
解题方法
4 . 我国著名的数学家秦九韶在《数书九章》提出了“三斜求积术”.他把三角形的三条边分别称为小斜、中斜和大斜.三斜求积术就是用小斜平方加上大斜平方,送到中斜平方,取相减后余数的一半,自乘而得一个数,小斜平方乘以大斜平方,送到上面得到的那个数,相减后余数被4除,所得的数作为“实”,1作为“隅”,开平方后即得面积.所谓“实”、“隅”指的是在方程 中,p为“隅”,q为“实”.即若
中,p为“隅”,q为“实”.即若 的大斜、中斜、小斜分别为a,b,c,则
的大斜、中斜、小斜分别为a,b,c,则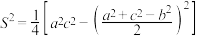 .已知点D是
.已知点D是 边AB上一点,
边AB上一点, ,
, ,
,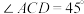 ,
,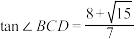 ,则
,则 的面积为
的面积为________ .
 中,p为“隅”,q为“实”.即若
中,p为“隅”,q为“实”.即若 的大斜、中斜、小斜分别为a,b,c,则
的大斜、中斜、小斜分别为a,b,c,则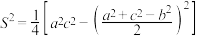 .已知点D是
.已知点D是 边AB上一点,
边AB上一点, ,
, ,
,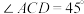 ,
,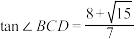 ,则
,则 的面积为
的面积为
您最近一年使用:0次
2020-03-21更新
|
1123次组卷
|
13卷引用:云南省昆明市外国语学校2020-2021学年高一4月月考数学试题
云南省昆明市外国语学校2020-2021学年高一4月月考数学试题山西省临汾市2020届高三下学期模拟考试(3)数学(文)试题2020届湖北省黄冈中学高三下学期4月高考模拟测试数学(理)试题辽宁省六校协作体2020-2021学年高二上学期期初考试数学试题福建省福清西山学校高中部2021届高三9月月考数学试题黑龙江省哈尔滨市第三中学2020-2021学年高三上学期期中考试理科数学试题江苏省南京市第一中学2020-2021学年高三上学期1月阶段性检测数学试题(已下线)专题05三角函数与解三角形(测)-2021年高考数学二轮复习讲练测(新高考版)(已下线)专题05 三角函数与解三角形(测)-2021年高考数学二轮复习讲练测(文理通用)(已下线)【新东方】双师193高一下湖北省新高考联考协作体2020-2021学年高一下学期期末数学试题安徽省六安市霍邱县第一中学2020-2021学年高一下学期段考数学试题(已下线)专题14 解三角形的综合问题-【重难点突破】2021-2022学年高一数学常考题专练(人教A版2019必修第二册)
5 . 赵爽是我国古代数学家、天文学家,大约在公元222年,赵爽为《周髀算经》一书作序时,介绍了“勾股圆方图”,亦称“赵爽弦图”(以弦为边长得到的正方形是由4个全等的直角三角形再加上中间的一个小正方形组成的).类比“赵爽弦图”,可类似地构造如图所示的图形,它是由3个全等的三角形与中间的一个小等边三角形拼成的一个大等边三角形,设 ,若在大等边三角形中随机取一点,则此点取自小等边三角形的概率是
,若在大等边三角形中随机取一点,则此点取自小等边三角形的概率是
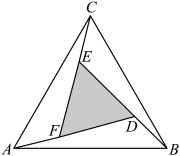
 ,若在大等边三角形中随机取一点,则此点取自小等边三角形的概率是
,若在大等边三角形中随机取一点,则此点取自小等边三角形的概率是
A.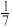 | B. | C. | D.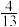 |
您最近一年使用:0次
2019-05-14更新
|
441次组卷
|
2卷引用:云南省昆明市第一中学2021届高三上学期高中新课标第四次一轮复习检测理科数学试题



