名校
解题方法
1 . 已知点O是 内部一点,并且满足
内部一点,并且满足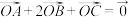 ,
, 的面积为
的面积为 ,
, 的面积为
的面积为 ,则
,则 ( )
( )
 内部一点,并且满足
内部一点,并且满足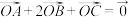 ,
, 的面积为
的面积为 ,
, 的面积为
的面积为 ,则
,则 ( )
( )| A.2 | B.3 | C. | D. |
您最近一年使用:0次
2023-05-12更新
|
2398次组卷
|
8卷引用:河南省安阳市林州市第一中学2023-2024学年高一下学期5月月考数学试题
河南省安阳市林州市第一中学2023-2024学年高一下学期5月月考数学试题四川省成都外国语学校2022-2023学年高一下学期期中考试数学试题(已下线)第01讲 平面向量专题期末高频考点题型秒杀(已下线)第五篇 向量与几何 专题13 奔驰定理 微点3 奔驰定理综合训练(已下线)2.2 从位移的合成到向量的加减法-同步精品课堂(北师大版2019必修第二册)江苏省无锡市江阴市两校联考2023-2024学年高一下学期4月期中考试数学试题江苏高一专题03平面向量(第二部分)广东实验中学2023-2024学年高一下学期第二次段考数学试题
2 . 如图为正八边形ABCDEFGH,其中O为正八边形的中心,则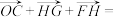 ( )
( )
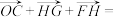 ( )
( )
A.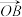 | B.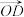 | C.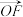 | D.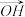 |
您最近一年使用:0次
2022-07-18更新
|
2386次组卷
|
13卷引用:河南省安阳市滑县2021-2022学年高一下学期期末数学试题
河南省安阳市滑县2021-2022学年高一下学期期末数学试题向量的加减法(已下线)6.2.1向量的加法运算(课件+作业)(已下线)9.2.1 向量的加减法1(已下线)6.2.1向量的加法运算(精讲)-【精讲精练】2022-2023学年高一数学下学期同步精讲精练(人教A版2019必修第二册)广东省佛山市顺德区容山中学2022-2023学年高一下学期3月月考数学试题(已下线)第01讲 平面向量的概念及线性运算4种题型(1)(已下线)6.3.2&6.3.3&6.3.4 平面向量的正交分解及坐标表示、平面向量加减法运算的坐标表示、平面向量的数乘运算及坐标表示(精练)(1)-【题型分类归纳】2022-2023学年高一数学同步讲与练(人教A版2019必修第二册)(已下线)第一节 平面向量的概念及线性运算 A素养养成卷(已下线)核心考点01平面向量及其应用(1)(已下线)6.2.1向量的加法运算【第三练】“上好三节课,做好三套题“高中数学素养晋级之路(已下线)6.2.1 向量的加法运算(分层作业)-【上好课】(已下线)6.2.1向量的加法运算——课后作业(巩固版)
名校
3 . 下列命题中,正确的是( )
A.若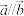 , ,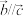 ,则 ,则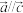 |
B.若 则 则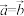 或 或 |
C.对于任意向量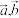 ,有 ,有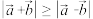 |
D.对于任意向量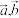 ,有 ,有 |
您最近一年使用:0次
2023-09-12更新
|
1144次组卷
|
10卷引用:河南省安阳市文峰区第一中学2021-2022学年高一下学期数学(文)期末考试试题
河南省安阳市文峰区第一中学2021-2022学年高一下学期数学(文)期末考试试题河南省安阳市林州市2021-2022学年高二下学期期末数学试题人教A版 必杀技 第二章 平面向量 第2.2节综合训练山东省临沂市罗庄区2021-2022学年高一下学期期中数学试题江西省丰城市东煌学校2022-2023学年高一下学期第二次月考数学试题(已下线)第一节 平面向量的概念及线性运算(讲)(已下线)6.2.2 向量的减法运算【第二课】“上好三节课,做好三套题“高中数学素养晋级之路(已下线)第03讲 6.2.2向量的减法运算-【帮课堂】(人教A版2019必修第二册)(已下线)6.2.2向量的减法运算(已下线)6.2.2?向量的减法运算——课后作业(基础版)
名校
解题方法
4 . 下列说法不正确的是( )
A.已知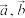 均为非零向量,则 均为非零向量,则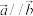  存在唯一的实数 存在唯一的实数 ,使得 ,使得 |
B.若向量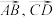 共线,则点 共线,则点 必在同一直线上 必在同一直线上 |
C.若 且 且 ,则 ,则 |
D.若点 为 为 的重心,则 的重心,则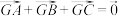 |
您最近一年使用:0次
2024-01-02更新
|
792次组卷
|
5卷引用:河南省安阳市龙安高级中学2023-2024学年高一下学期3月月考数学试卷
5 . 已知点 在
在 所在平面内,满足
所在平面内,满足 ,则点
,则点 是
是 的( )
的( )
 在
在 所在平面内,满足
所在平面内,满足 ,则点
,则点 是
是 的( )
的( )| A.外心 | B.内心 | C.垂心 | D.重心 |
您最近一年使用:0次
2024-07-25更新
|
648次组卷
|
11卷引用:河南省安阳市龙安高级中学2023-2024学年高一下学期期中考试数学试卷
河南省安阳市龙安高级中学2023-2024学年高一下学期期中考试数学试卷河南省许昌市2021-2022学年高一下学期期末数学理科试题河南省许昌市2021-2022学年高一下学期期末数学文科试题(已下线)6.1 平面向量的概念(精练)-2022-2023学年高一数学一隅三反系列(人教A版2019必修第二册)(已下线)微专题04 平面向量痛点问题之三角形“四心”问题(1)-【微专题】2022-2023学年高一数学常考点微专题提分精练(人教A版2019必修第二册)(已下线)专题9-1:平面向量与三角形的“四心”-【题型分类归纳】2022-2023学年高一数学同步讲与练(苏教版2019必修第二册)(已下线)平面向量专题:三角形“四心”的向量式问题-【题型分类归纳】2022-2023学年高一数学同步讲与练(人教A版2019必修第二册)(已下线)第6.1讲 平面向量的概念-精讲精练宝典重庆市长寿区2023-2024学年高一下学期期末考试数学试题(B卷)(已下线)重难点突破01 奔驰定理与四心问题(五大题型)安徽省安庆市怀宁县第二中学2023-2024学年高一下学期期中考试数学试卷
解题方法
6 . 已知 的外心为
的外心为 ,若
,若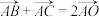 ,且
,且 ,则
,则
___________ .
 的外心为
的外心为 ,若
,若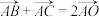 ,且
,且 ,则
,则
您最近一年使用:0次
2022-02-27更新
|
1528次组卷
|
4卷引用:河南省安阳市2021-2022学年高三下学期 (二模)阶段性测试(四)文科数学试题
名校
7 . 下列说法错误的是( )
A.向量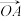 的长度与向量 的长度与向量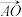 的长度相等 的长度相等 | B.零向量与任意非零向量平行 |
| C.长度相等方向相反的向量共线 | D.方向相反的向量可能相等 |
您最近一年使用:0次
2020-07-14更新
|
2157次组卷
|
15卷引用:河南省安阳市林州市2020-2021学年高一下学期期末数学试题
河南省安阳市林州市2020-2021学年高一下学期期末数学试题河北省衡水市桃城区第十四中学2019-2020学年高一下学期第一次综合测试数学试题(已下线)第27讲 平面向量的概念及线性运算-2021年新高考数学一轮专题复习(新高考专版)(已下线)考点26 平面向量的概念、平面向量的基本运算(考点专练)-备战2021年新高考数学一轮复习考点微专题(已下线)专题6.1 平面向量的概念及其线性运算(讲)-2021年新高考数学一轮复习讲练测(已下线)专题6.1 平面向量及其线性运算(A卷基础篇)-2020-2021学年高一数学必修第二册同步单元AB卷(新教材人教A版,浙江专用)(已下线)6.1.1 向量的概念-2020-2021学年高一数学课时同步练(人教B版2019必修第二册)(已下线)专题6.1平面向量及其线性运算(A卷基础篇)-2020-2021学年高一数学必修第二册同步单元AB卷(新教材人教B版)浙江省湖州市德清县第三中学2020-2021学年高一下学期3月月考数学试题福建省福州市福清市西山学校2020-2021学年高一3月月考数学试题福建省永泰县第三中学2020-2021学年高一4月月考数学试题北师大版(2019) 必修第二册 金榜题名 第二章 单元素养评价(已下线)专题6.1 平面向量的概念及其运算(讲)- 2022年高考数学一轮复习讲练测(新教材新高考)黑龙江省牡丹江市第二高级中学2022-2023学年高一下学期4月月考数学试题甘肃省定西市临洮中学2023-2024学年高一下学期第一次月考数学试卷
8 . 如图所示, 的三边均不相等,E,F,D分别是AC,AB,BC的中点,在以A,B,C,D,E,F为起点或终点的所有有向线段表示的向量中:
的三边均不相等,E,F,D分别是AC,AB,BC的中点,在以A,B,C,D,E,F为起点或终点的所有有向线段表示的向量中: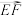 相反的向量;
相反的向量;
(2)写出与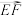 的模相等的向量;
的模相等的向量;
(3)写出与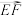 相等的向量.
相等的向量.
 的三边均不相等,E,F,D分别是AC,AB,BC的中点,在以A,B,C,D,E,F为起点或终点的所有有向线段表示的向量中:
的三边均不相等,E,F,D分别是AC,AB,BC的中点,在以A,B,C,D,E,F为起点或终点的所有有向线段表示的向量中: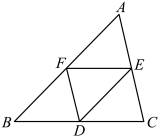
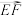 相反的向量;
相反的向量;(2)写出与
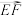 的模相等的向量;
的模相等的向量;(3)写出与
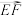 相等的向量.
相等的向量.
您最近一年使用:0次
2023-06-11更新
|
477次组卷
|
3卷引用:河南省安阳市龙安高级中学2022-2023学年高一下学期3月月考数学试卷
河南省安阳市龙安高级中学2022-2023学年高一下学期3月月考数学试卷2023版 湘教版(2019) 必修第二册 过关斩将 第1章 1.1 向量(已下线)第01讲 6.1平面向量的概念-【帮课堂】(人教A版2019必修第二册)
名校
解题方法
9 . 下列结论中,正确的是( )
A. 长的有向线段不可能表示单位向量 长的有向线段不可能表示单位向量 |
B.若O是直线l上的一点,单位长度已选定,则l上有且只有两个点A,B,使得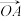 , ,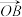 是单位向量 是单位向量 |
| C.方向为北偏西30°的向量与南偏东30°的向量不可能是共线向量 |
D.一人从A点向东走500米到达B点,则向量 不能表示这个人从A点到B点的位移 不能表示这个人从A点到B点的位移 |
您最近一年使用:0次
2022-08-19更新
|
783次组卷
|
6卷引用:河南省安阳市林州市第一中学2022-2023学年高一下学期期末数学试题
河南省安阳市林州市第一中学2022-2023学年高一下学期期末数学试题苏教版(2019) 必修第二册 过关斩将 第9章 9.1 向量概念(已下线)第01讲 平面向量的概念及其线性运算 (高频考点—精练)(已下线)9.1 向量概念(分层练习)-2022-2023学年高一数学同步精品课堂(苏教版2019必修第二册)(已下线)专题6.2 平面向量的概念(重难点题型检测)-2022-2023学年高一数学举一反三系列(人教A版2019必修第二册)(已下线)专题01 平面向量及其应用(1)-期末真题分类汇编(新高考专用)
名校
10 . 已知向量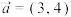 ,
, ,
,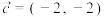 .
.
(1)若 ,求实数m,n的值;
,求实数m,n的值;
(2)若 ,求实数k的值.
,求实数k的值.
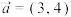 ,
, ,
,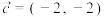 .
.(1)若
 ,求实数m,n的值;
,求实数m,n的值;(2)若
 ,求实数k的值.
,求实数k的值.
您最近一年使用:0次
2022-05-03更新
|
611次组卷
|
4卷引用:河南省安阳市第一中学2021-2022学年高一下学期第二次阶段考试数学试题



