名校
1 . 在平面直角坐标系中,直线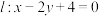 与抛物线
与抛物线 相切.
相切.
(1)求 的值;
的值;
(2)若点 为
为 的焦点,点
的焦点,点 为
为 的准线上一点.过点
的准线上一点.过点 的两条直线
的两条直线 ,
, 分别与
分别与 相切,直线
相切,直线 与
与 ,
, 分别相交于
分别相交于 ,
, ,求证:
,求证: .
.
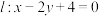 与抛物线
与抛物线 相切.
相切.(1)求
 的值;
的值;(2)若点
 为
为 的焦点,点
的焦点,点 为
为 的准线上一点.过点
的准线上一点.过点 的两条直线
的两条直线 ,
, 分别与
分别与 相切,直线
相切,直线 与
与 ,
, 分别相交于
分别相交于 ,
, ,求证:
,求证: .
.
您最近半年使用:0次
2023-11-23更新
|
503次组卷
|
4卷引用:江苏省南通市如东高级中学2024届高三上学期期中学情检测数学试题
江苏省南通市如东高级中学2024届高三上学期期中学情检测数学试题江苏省南通市如东县2024届高三上学期期中数学试题(已下线)专题03 圆锥曲线的方程(2)(已下线)重难点7-2 圆锥曲线综合应用(7题型+满分技巧+限时检测)
名校
2 . 点O在△ 所在的平面内,则以下说法正确的是( )
所在的平面内,则以下说法正确的是( )
 所在的平面内,则以下说法正确的是( )
所在的平面内,则以下说法正确的是( )A.已知平面向量 满足 满足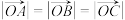 ,且 ,且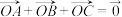 ,则△ ,则△ 是等边三角形 是等边三角形 |
B.若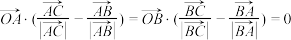 ,则点O为△ ,则点O为△ 的重心 的重心 |
C.若 ,则点O为△ ,则点O为△ 的外心; 的外心; |
D.若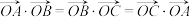 ,则点O为△ ,则点O为△ 的垂心 的垂心 |
您最近半年使用:0次
名校
解题方法
3 . 点 在△
在△ 所在的平面内,则以下说法正确的有( )
所在的平面内,则以下说法正确的有( )
 在△
在△ 所在的平面内,则以下说法正确的有( )
所在的平面内,则以下说法正确的有( )A.若动点 满足 满足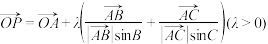 ,则动点 ,则动点 的轨迹一定经过△ 的轨迹一定经过△ 的垂心; 的垂心; |
B.若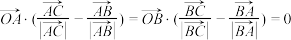 ,则点 ,则点 为△ 为△ 的内心; 的内心; |
C.若 ,则点 ,则点 为△ 为△ 的外心; 的外心; |
D.若动点 满足 满足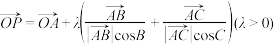 ,则动点 ,则动点 的轨迹一定经过△ 的轨迹一定经过△ 的重心. 的重心. |
您最近半年使用:0次
2021-08-03更新
|
2805次组卷
|
10卷引用:安徽省黄山市2020-2021学年高一下学期期末数学试题
安徽省黄山市2020-2021学年高一下学期期末数学试题(已下线)专题03 平面向量(数学思想与方法)-备战2022年高考数学二轮复习重难考点专项突破训练(全国通用)(已下线)第6章 平面向量及其应用(压轴30题专练)-2021-2022学年高一数学考试满分全攻略(人教A版2019必修第二册)江苏省苏州中学2021-2022学年高一下学期期中数学试题黑龙江省哈尔滨市阿城区第一中学2021-2022学年高一6月月考数学试题黑龙江省哈尔滨市阿城区第一中学2021-2022学年高一6月月考数学试题(已下线)重难点04五种平面向量数学思想-2(已下线)高一数学下学期期中模拟试卷(第9-12章)-【题型分类归纳】2022-2023学年高一数学同步讲与练(苏教版2019必修第二册)福建省福州市福清西山学校2022-2023学年高一下学期5月月考数学试题专题03平面向量在几何中的应用
解题方法
4 . 已知 外接圆的圆心为O,半径为1.设点O到边
外接圆的圆心为O,半径为1.设点O到边 ,
, ,
, 的距离分别为
的距离分别为 ,
,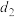 ,
,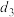 .若
.若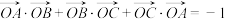 ,则
,则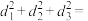 ( )
( )
 外接圆的圆心为O,半径为1.设点O到边
外接圆的圆心为O,半径为1.设点O到边 ,
, ,
, 的距离分别为
的距离分别为 ,
,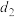 ,
,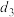 .若
.若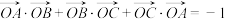 ,则
,则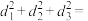 ( )
( )A. | B.1 | C. | D.3 |
您最近半年使用:0次
2021-08-02更新
|
2594次组卷
|
4卷引用:江苏省泰州市2020-2021学年高一下学期期末数学试题
江苏省泰州市2020-2021学年高一下学期期末数学试题(已下线)第6章 平面向量及其应用(压轴30题专练)-2021-2022学年高一数学考试满分全攻略(人教A版2019必修第二册)浙江省杭州市S9联盟2022-2023学年高二上学期11月期中联考数学试题(已下线)第六章 平面向量及其应用(基础、典型、易错、压轴)分类专项训练(3)
名校
解题方法
5 . 数学探究:用向量法研究三角形的性质.向量集数与形于一身,每一种向量运算都有相应的几何意义.向量运算与几何图形性质的内在联系,使我们自然想到:利用向量运算研究几何图形的性质,是否会更加方便、便捷呢?在数学研究中,常常用新的工具、新的方法对已研究过的对象进行再研究,这不仅可以站在新的高度审视研究对象,而且还可以有所发现.三角形是几何中最简单的封闭图形,但它是最重要的基本几何图形之一.三角形的性质非常丰富,是联系各种几何图形的纽带.在平面几何中,我们已经研究过三角形的一些基本性质,但对三角形的认识还不够深入,例如对三角形的外心、中线、重心、角平分线、内心、高、垂心等只有初步认识.因此,以向量为工具对三角形进行再研究是非常有意义的. ,
, 表示).
表示).
(2) 中,
中,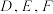 分别是
分别是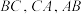 的中点,O是重心,证明:对任意一点P,向量
的中点,O是重心,证明:对任意一点P,向量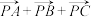 与
与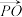 共线.
共线.
(3)我们知道,三角形的三条中线交于一点,这一点就是三角形的重心,请你从下面两个问题中任选一个并解答(注:如果选择两个,则按第一个解答计分)①用向量方法证明:三角形的三条高线交于一点.如图①所示, 中,设
中,设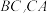 边上的高
边上的高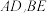 交于点H,求证:边
交于点H,求证:边 上的高过点H;②用向量方法证明:三角形的三边的垂直平分线交于一点.如图②所示,
上的高过点H;②用向量方法证明:三角形的三边的垂直平分线交于一点.如图②所示, 的三边
的三边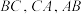 的中点分别为
的中点分别为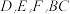 和
和 边上的垂直平分线交于点O,求证:
边上的垂直平分线交于点O,求证: 边上的垂直平分线过点O.
边上的垂直平分线过点O.
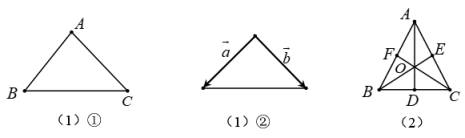
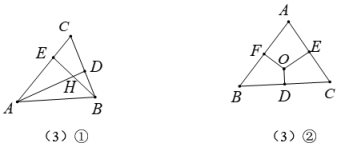
 ,
, 表示).
表示).(2)
 中,
中,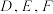 分别是
分别是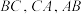 的中点,O是重心,证明:对任意一点P,向量
的中点,O是重心,证明:对任意一点P,向量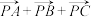 与
与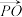 共线.
共线.(3)我们知道,三角形的三条中线交于一点,这一点就是三角形的重心,请你从下面两个问题中任选一个并解答(注:如果选择两个,则按第一个解答计分)①用向量方法证明:三角形的三条高线交于一点.如图①所示,
 中,设
中,设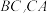 边上的高
边上的高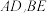 交于点H,求证:边
交于点H,求证:边 上的高过点H;②用向量方法证明:三角形的三边的垂直平分线交于一点.如图②所示,
上的高过点H;②用向量方法证明:三角形的三边的垂直平分线交于一点.如图②所示, 的三边
的三边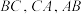 的中点分别为
的中点分别为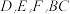 和
和 边上的垂直平分线交于点O,求证:
边上的垂直平分线交于点O,求证: 边上的垂直平分线过点O.
边上的垂直平分线过点O.
您最近半年使用:0次
名校
解题方法
6 . 动点P到定点F(0,1)的距离比它到直线 的距离小1,设动点P的轨迹为曲线C,过点F的直线交曲线C于A、B两个不同的点,过点A、B分别作曲线C的切线,且二者相交于点M.
的距离小1,设动点P的轨迹为曲线C,过点F的直线交曲线C于A、B两个不同的点,过点A、B分别作曲线C的切线,且二者相交于点M.
(1)求曲线C的方程;
(2)求证: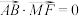 ;
;
(3)求△ ABM的面积的最小值.
 的距离小1,设动点P的轨迹为曲线C,过点F的直线交曲线C于A、B两个不同的点,过点A、B分别作曲线C的切线,且二者相交于点M.
的距离小1,设动点P的轨迹为曲线C,过点F的直线交曲线C于A、B两个不同的点,过点A、B分别作曲线C的切线,且二者相交于点M.(1)求曲线C的方程;
(2)求证:
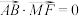 ;
;(3)求△ ABM的面积的最小值.
您最近半年使用:0次
2018-01-12更新
|
1199次组卷
|
7卷引用:湖北省襄阳市2018届高三1月调研统一测试数学(文)试题
湖北省襄阳市2018届高三1月调研统一测试数学(文)试题(已下线)《2018届优生-百日闯关系列》数学专题三 第三关 以解析几何中与抛物线相关的综合问题湖北省襄阳市2018届高三1月调研统一测试数学(理)试题湖北省黄冈中学2022届高三下学期二模数学试题湖北省黄冈市重点中学2022届高三下学期5月二模数学试题四川省宜宾市叙州区第二中学校2024届高三上学期期末数学(理)试题四川省宜宾市叙州区第二中学校2024届高三上学期期末数学(文)试题



