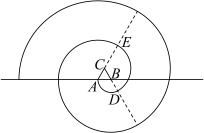
1 . 蚊香具有悠久的历史,我国蚊香的发明与古人端午节的习俗有关.如图为某校数学社团用数学软件制作的“蚊香”. 画法如下:在水平直线上取长度为1的线段 ,作一个等边三角形
,作一个等边三角形 ,然后以点B为圆心,
,然后以点B为圆心, 为半径逆时针画圆弧交线段
为半径逆时针画圆弧交线段 的延长线于点D(第一段圆弧),再以点C为圆心,
的延长线于点D(第一段圆弧),再以点C为圆心, 为半径逆时针画圆弧交线段
为半径逆时针画圆弧交线段 的延长线于点E,再以点A为圆心,
的延长线于点E,再以点A为圆心, 为半径逆时针画圆弧……以此类推,当得到的“蚊香”恰好有15段圆弧时,“蚊香”的长度为( )
为半径逆时针画圆弧……以此类推,当得到的“蚊香”恰好有15段圆弧时,“蚊香”的长度为( )
 ,作一个等边三角形
,作一个等边三角形 ,然后以点B为圆心,
,然后以点B为圆心, 为半径逆时针画圆弧交线段
为半径逆时针画圆弧交线段 的延长线于点D(第一段圆弧),再以点C为圆心,
的延长线于点D(第一段圆弧),再以点C为圆心, 为半径逆时针画圆弧交线段
为半径逆时针画圆弧交线段 的延长线于点E,再以点A为圆心,
的延长线于点E,再以点A为圆心, 为半径逆时针画圆弧……以此类推,当得到的“蚊香”恰好有15段圆弧时,“蚊香”的长度为( )
为半径逆时针画圆弧……以此类推,当得到的“蚊香”恰好有15段圆弧时,“蚊香”的长度为( )
A.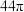 | B. | C.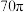 | D.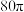 |
您最近一年使用:0次
2024-01-11更新
|
3006次组卷
|
11卷引用:信息必刷卷02(江苏专用,2024新题型)
(已下线)信息必刷卷02(江苏专用,2024新题型)江西省抚州市金溪一中2024届高三上学期1月考试数学试题广东省广州市广东实验中学2024届高三上学期大湾区数学冲刺卷(五)河北省部分学校2024届高三上学期摸底考试数学试题(已下线)考点20 三角函数的数学文化 --2024届高考数学考点总动员【练】(已下线)新题型01 新高考新结构二十一大考点汇总-3(已下线)(新高考新结构)2024年高考数学模拟卷(三)(已下线)专题06 数列新疆生产建设兵团第三师图木舒克市第一中学2023-2024学年高二下学期数学开学考试数学试卷海南省琼海市嘉积中学2023-2024学年高三下学期高中教学第三次大课堂练习数学试题(已下线)第02讲 等差数列及其前n项和(十大题型)(讲义)
2 . 《张邱建算经》记载:今有女子不善织布,逐日织布同数递减,初日织五尺,末一日织一尺,计织三十日,问共织布__________ 尺.
您最近一年使用:0次
2023-10-06更新
|
576次组卷
|
4卷引用:江苏省徐州市铜山区铜北中学2023-2024学年高二上学期第一次月考数学试题
3 . 南宋数学家杨辉所著的《详解九章算法·商功》中描述了如图所示的形状,后人称为“三角垛”.三角垛的最上层(即第一层)有1个球,第二层有3个球,第三层有6个球,…,从第二层开始,每层球数与上一层球数之差依次构成等差数列.现有60个篮球,把它们堆放成一个三角垛,那么剩余篮球的个数最少为______ .


您最近一年使用:0次
2023-07-06更新
|
559次组卷
|
3卷引用:4.2 等差数列(3)
4 . 《张邱建算经》有一道题:今有女子不善织布,逐日所织的布同数递减,初日织五尺,末一日织一尺,计织三十日,问共织布( )
| A.110尺 | B.90尺 | C.60尺 | D.30尺 |
您最近一年使用:0次
解题方法
5 . 我国古代数学著作《算法统宗》中有如下问题:“今有善走者,日增等里,首日行走一百里,九日共行一千二百六十里,问日增几何?”其大意是:现有一位善于步行的人,第一天行走了一百里,以后每天比前一天多走 里,九天他共行走了一千二百六十里,求d的值.关于该问题,下列结论错误的是( )
里,九天他共行走了一千二百六十里,求d的值.关于该问题,下列结论错误的是( )
 里,九天他共行走了一千二百六十里,求d的值.关于该问题,下列结论错误的是( )
里,九天他共行走了一千二百六十里,求d的值.关于该问题,下列结论错误的是( )A. | B.此人第三天行走了一百三十里 |
| C.此人前七天共行走了九百一十里 | D.此人前八天共行走了一千零八十里 |
您最近一年使用:0次
名校
6 . 公元前1800年,古埃及的“加罕纸草书”上有这样一个问题:将100德本(德本是古埃及的重量单位)的食物分成10份,第一份最大,从第二份开始,每份比前一份少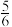 德本,求各份的大小.在这个问题中,最小的一份是
德本,求各份的大小.在这个问题中,最小的一份是______ 德本.
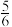 德本,求各份的大小.在这个问题中,最小的一份是
德本,求各份的大小.在这个问题中,最小的一份是
您最近一年使用:0次
2023-06-19更新
|
304次组卷
|
4卷引用:4.2 等差数列(3)
7 . 我国古代数学家提出的“中国剩余定理”又称“孙子定理”,它是世界数学史上光辉的一页,定理涉及的是整除问题.现有如下一个整除问题:将1至2023这2023个数中,能被3除余1且被5除余2的数按从小到大的顺序排成一列,构成数列 ,则此数列的项数为( )
,则此数列的项数为( )
 ,则此数列的项数为( )
,则此数列的项数为( )| A.133项 | B.134项 | C.135项 | D.136项 |
您最近一年使用:0次
名校
解题方法
8 . 一百零八塔,位于宁夏吴忠青铜峡市,是始建于西夏时期的喇嘛式实心塔群,是中国现存最大且排列最整齐的喇嘛塔群之一,塔的排列顺序自上而下,第一层1座,第二层3座,第三层3座,第四层5座,第五层5座,从第五层开始,每一层塔的数目构成一个首项为5,公差为2的等差数列,总计一百零八座,则该塔共有( )
| A.八层 | B.十层 | C.十一层 | D.十二层 |
您最近一年使用:0次
2023-05-21更新
|
634次组卷
|
5卷引用:江苏省镇江市丹阳高级中学2022-2023学年高二下学期期中数学试题
江苏省镇江市丹阳高级中学2022-2023学年高二下学期期中数学试题(已下线)专题18 数列中的创新题的解法 微点2 数列中的创新题综合训练黑龙江省哈尔滨市第一中学校2023-2024学年高二上学期期末考试数学试卷(已下线)第4.2.2讲 等差数列前n项和的应用(第2课时)-2023-2024学年新高二数学同步精讲精练宝典(人教A版2019选修第二、三册)(已下线)模块3 专题1 第3套 小题入门夯实练【高二人教B】
9 . “中国剩余定理”一般指“孙子定理”,是中国古代求解一次同余式组的方法,是数论中一个重要定理,若将被3除余2且被5除余2的正整数从小到大排列,组成数列 ,则
,则 为( )
为( )
 ,则
,则 为( )
为( )A. | B.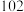 | C. | D.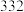 |
您最近一年使用:0次
名校
10 . 《九章算术》是我国古代的数学名著,书中有如下问题:“今有女子善织,日增等尺,三日织9尺,第二日、第四日、第六日所织之和为15尺,则其七日共织尺数为几何?”大致意思是:“有一女子善于织布,每日增加相同的尺数,前三日共织布9尺,第二日、第四日、第六日所织布之和为15尺,问她前七日共织布多少尺?” ( )
| A.28 | B.32 | C.35 | D.42 |
您最近一年使用:0次
2023-01-08更新
|
399次组卷
|
5卷引用:专题06 等差数列及其前n项和8种常见考法归类(1)
(已下线)专题06 等差数列及其前n项和8种常见考法归类(1)安徽省合肥市庐江县2021-2022学年高二上学期期末数学试题(已下线)山东省青岛第二中学2022-2023学年高三上学期1月期末测试数学试题变式题1-5四川省内江市威远中学校2022-2023学年高三下学期第一次月考数学(理)试题四川省内江市威远中学校2022-2023学年高三下学期第一次月考数学(文)试题



