1 . 已知数列 满足
满足 ,
,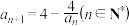 .
.
(1)求证: 是等差数列;
是等差数列;
(2)若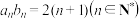 ,求数列
,求数列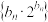 的前n项和
的前n项和 .
.
 满足
满足 ,
,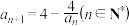 .
.(1)求证:
 是等差数列;
是等差数列;(2)若
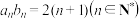 ,求数列
,求数列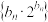 的前n项和
的前n项和 .
.
您最近一年使用:0次
2022-01-18更新
|
634次组卷
|
4卷引用:甘肃省庆阳市华池县第一中学2023-2024学年高二上学期期末考试数学试题
甘肃省庆阳市华池县第一中学2023-2024学年高二上学期期末考试数学试题山西省太原市2021-2022学年高二上学期期末数学试题(已下线)解密11 数列的前n项和及其应用(分层训练)-【高频考点解密】2022年高考数学二轮复习讲义+分层训练(全国通用)云南省楚雄彝族自治州民族中学2022-2023学年高二下学期6月月考数学试题
名校
2 . 已知四边形 内接于圆
内接于圆 ,
,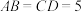 ,
, ,
,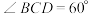 .
.

(1)求证: 的三边长度可以构成一个等差数列;
的三边长度可以构成一个等差数列;
(2)求 的面积.
的面积.
 内接于圆
内接于圆 ,
,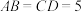 ,
, ,
,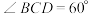 .
.
(1)求证:
 的三边长度可以构成一个等差数列;
的三边长度可以构成一个等差数列;(2)求
 的面积.
的面积.
您最近一年使用:0次
2021-09-12更新
|
410次组卷
|
3卷引用:甘肃省嘉陵关市第一中学2020-2021学年高三下学期六模考试数学(文)试题
3 . 已知数列 满足
满足 ,
,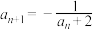 .
.
(1)求证数列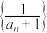 为等差数列;
为等差数列;
(2)求数列 的通项公式.
的通项公式.
 满足
满足 ,
, .
.(1)求证数列
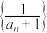 为等差数列;
为等差数列;(2)求数列
 的通项公式.
的通项公式.
您最近一年使用:0次
2021-09-15更新
|
1403次组卷
|
4卷引用:甘肃省甘南藏族自治州合作第一中学2021-2022学年高二上学期期中考试数学(文)试题
4 . 已知数列 中,
中,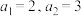 ,其前
,其前 项和
项和 满足
满足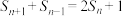 ,其中
,其中 ,
, .
.
(1)求证:数列 为等差数列,并求其通项公式.
为等差数列,并求其通项公式.
(2)设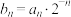 ,
, 为数列
为数列 的前n项和,求
的前n项和,求 的最小值.
的最小值.
 中,
中,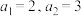 ,其前
,其前 项和
项和 满足
满足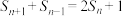 ,其中
,其中 ,
, .
.(1)求证:数列
 为等差数列,并求其通项公式.
为等差数列,并求其通项公式.(2)设
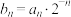 ,
, 为数列
为数列 的前n项和,求
的前n项和,求 的最小值.
的最小值.
您最近一年使用:0次
2023高三·全国·专题练习
解题方法
5 . 记数列 的前
的前 项和为
项和为 ,
, ,
, ,
,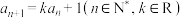 .证明数列
.证明数列 为等差数列,并求通项公式
为等差数列,并求通项公式 ;
;
 的前
的前 项和为
项和为 ,
, ,
, ,
,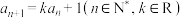 .证明数列
.证明数列 为等差数列,并求通项公式
为等差数列,并求通项公式 ;
;
您最近一年使用:0次
6 . 已知数列{ }满足
}满足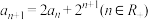 ,且
,且 .
.
(I)证明:数列{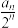 }是等差数列;
}是等差数列;
(II)求数列{ }的前
}的前 项和
项和 .
.
 }满足
}满足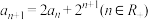 ,且
,且 .
.(I)证明:数列{
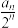 }是等差数列;
}是等差数列;(II)求数列{
 }的前
}的前 项和
项和 .
.
您最近一年使用:0次
2019-09-13更新
|
2204次组卷
|
2卷引用:甘肃省天水市第一中学2019-2020学年高二上学期第二次学段(期中)考试数学(理)试题



