1 . 在正四棱柱 中,
中, ,
,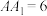 ,M,N分别是
,M,N分别是 ,
, 的中点,则平面
的中点,则平面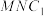 截该四棱柱所得截面的周长为
截该四棱柱所得截面的周长为______ .
 中,
中, ,
,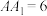 ,M,N分别是
,M,N分别是 ,
, 的中点,则平面
的中点,则平面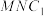 截该四棱柱所得截面的周长为
截该四棱柱所得截面的周长为
您最近一年使用:0次
名校
解题方法
2 . 如图,在正方体 中,
中,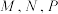 分别为
分别为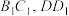 和
和 的中点,则下列说法正确的序号有
的中点,则下列说法正确的序号有______ . ,
, ,
, ,
, 四点共面;②
四点共面;②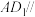 平面
平面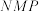 ;③
;③ 与
与 所成角为
所成角为 .
.
 中,
中,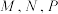 分别为
分别为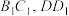 和
和 的中点,则下列说法正确的序号有
的中点,则下列说法正确的序号有
 ,
, ,
, ,
, 四点共面;②
四点共面;②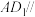 平面
平面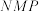 ;③
;③ 与
与 所成角为
所成角为 .
.
您最近一年使用:0次
名校
3 . 如图,直四棱柱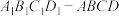 的底面是边长为2的正方形,
的底面是边长为2的正方形, ,
, ,
, 分别是
分别是 ,
,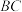 的中点,
的中点, 为直四棱柱表面上的动点,若
为直四棱柱表面上的动点,若 ,
, ,
, ,
, 四点共面,则动点P的轨迹的长度为
四点共面,则动点P的轨迹的长度为______ .
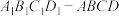 的底面是边长为2的正方形,
的底面是边长为2的正方形, ,
, ,
, 分别是
分别是 ,
,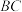 的中点,
的中点, 为直四棱柱表面上的动点,若
为直四棱柱表面上的动点,若 ,
, ,
, ,
, 四点共面,则动点P的轨迹的长度为
四点共面,则动点P的轨迹的长度为
您最近一年使用:0次
名校
4 . 正方体 棱长为2,N为线段
棱长为2,N为线段 上一动点,
上一动点, 为线段
为线段 上一动点,则
上一动点,则 的最小值为
的最小值为____________ .
 棱长为2,N为线段
棱长为2,N为线段 上一动点,
上一动点, 为线段
为线段 上一动点,则
上一动点,则 的最小值为
的最小值为
您最近一年使用:0次
5 . 在以底面为等腰直角三角形的直三棱柱 中,
中, 为底面三角形斜边
为底面三角形斜边 上一点,且
上一点,且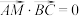 ,
,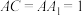 ,
, 为线段
为线段 上一动点,则平面
上一动点,则平面 截三棱柱所得截面面积的最大值为
截三棱柱所得截面面积的最大值为
______ .
 中,
中, 为底面三角形斜边
为底面三角形斜边 上一点,且
上一点,且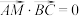 ,
,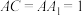 ,
, 为线段
为线段 上一动点,则平面
上一动点,则平面 截三棱柱所得截面面积的最大值为
截三棱柱所得截面面积的最大值为
您最近一年使用:0次
2024高一下·全国·专题练习
解题方法
6 . 如图,已知四面体ABCD的各条棱长均等于4,E,F分别是棱AD、BC的中点.若用一个与直线EF垂直,且与四面体的每一个面都相交的平面 去截该四面体,由此得到一个多边形截面,则该多边形截面面积最大值为
去截该四面体,由此得到一个多边形截面,则该多边形截面面积最大值为_________ .
 去截该四面体,由此得到一个多边形截面,则该多边形截面面积最大值为
去截该四面体,由此得到一个多边形截面,则该多边形截面面积最大值为
您最近一年使用:0次
2024高一下·全国·专题练习
7 . 给出下列命题:①书桌面是平面; ②平面 与平面
与平面 相交,它们只有有限个公共点;③如果两个平面有三个不共线的公共点,那么这两个平面重合. 正确的是
相交,它们只有有限个公共点;③如果两个平面有三个不共线的公共点,那么这两个平面重合. 正确的是_________ (填写序号).
 与平面
与平面 相交,它们只有有限个公共点;③如果两个平面有三个不共线的公共点,那么这两个平面重合. 正确的是
相交,它们只有有限个公共点;③如果两个平面有三个不共线的公共点,那么这两个平面重合. 正确的是
您最近一年使用:0次
名校
8 . 如图,正方体 的棱长为1,
的棱长为1, 为
为 的中点,
的中点, 为线段
为线段 上的动点,过点
上的动点,过点 ,
, ,
, 的平面截该正方体所得截面记为
的平面截该正方体所得截面记为 ,则下列命题正确的是
,则下列命题正确的是 _____ (写出所有正确命题的编号)
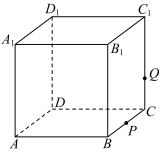
①当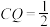 时,
时, 为等腰梯形.
为等腰梯形.
②当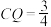 时,
时, 与
与 的交点
的交点 满足
满足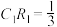 .
.
③当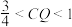 时,
时, 为四边形.
为四边形.
④当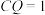 时,
时, 的面积为
的面积为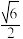 .
.
 的棱长为1,
的棱长为1, 为
为 的中点,
的中点, 为线段
为线段 上的动点,过点
上的动点,过点 ,
, ,
, 的平面截该正方体所得截面记为
的平面截该正方体所得截面记为 ,则下列命题正确的是
,则下列命题正确的是 
①当
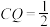 时,
时, 为等腰梯形.
为等腰梯形.②当
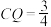 时,
时, 与
与 的交点
的交点 满足
满足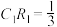 .
.③当
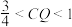 时,
时, 为四边形.
为四边形.④当
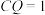 时,
时, 的面积为
的面积为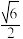 .
.
您最近一年使用:0次
2024-03-22更新
|
685次组卷
|
3卷引用:广东省广州市第六十五中学2023-2024学年高一下学期期中考试数学试卷
2024高三·全国·专题练习
9 . 如图,在正方 中,
中, 分别是
分别是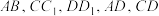 的中点,存在过点
的中点,存在过点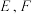 的平面
的平面 与平面
与平面 平行,平面
平行,平面 截该正方体得到的截面面积为
截该正方体得到的截面面积为______
 中,
中, 分别是
分别是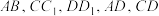 的中点,存在过点
的中点,存在过点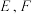 的平面
的平面 与平面
与平面 平行,平面
平行,平面 截该正方体得到的截面面积为
截该正方体得到的截面面积为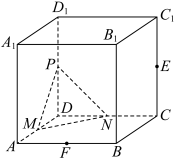
您最近一年使用:0次
2024高三·全国·专题练习
10 . 如图所示,在棱长为2的正方体 中,点
中,点 ,
, 分别为棱
分别为棱 ,
, 上的动点(包含端点),当
上的动点(包含端点),当 ,
, 分别为棱
分别为棱 ,
, 的中点时,则过
的中点时,则过 ,
, ,
, 三点作正方体的截面,所得截面为
三点作正方体的截面,所得截面为______ 边形.
 中,点
中,点 ,
, 分别为棱
分别为棱 ,
, 上的动点(包含端点),当
上的动点(包含端点),当 ,
, 分别为棱
分别为棱 ,
, 的中点时,则过
的中点时,则过 ,
, ,
, 三点作正方体的截面,所得截面为
三点作正方体的截面,所得截面为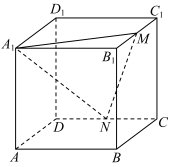
您最近一年使用:0次



