名校
1 . 如图,在四棱锥 中,
中,
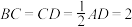 ,
, 为棱
为棱 的中点,
的中点, 平面
平面 .
.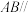 平面
平面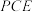
(2)求证:平面 平面
平面
(3)若二面角 的大小为
的大小为 ,求直线
,求直线 与平面
与平面 所成角的正切值.
所成角的正切值.
 中,
中,
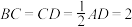 ,
, 为棱
为棱 的中点,
的中点, 平面
平面 .
.
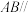 平面
平面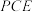
(2)求证:平面
 平面
平面
(3)若二面角
 的大小为
的大小为 ,求直线
,求直线 与平面
与平面 所成角的正切值.
所成角的正切值.
您最近一年使用:0次
2023-01-08更新
|
5247次组卷
|
11卷引用:辽宁省沈阳市东北育才学校2023-2024学年高一下学期5月月考数学试卷
辽宁省沈阳市东北育才学校2023-2024学年高一下学期5月月考数学试卷天津市宁河区芦台第四中学2019-2020学年高三上学期第二次月考数学试题第8章 立体几何初步 章末测试(提升)-2022-2023学年高一数学一隅三反系列(人教A版2019必修第二册)(已下线)专题8.16 空间角大题专项训练(30道)-2022-2023学年高一数学举一反三系列(人教A版2019必修第二册)广东省汕头市2022-2023学年高一下学期期末数学试题山东省滨州市高新高级中学2022-2023学年高一下学期期中考试数学试题单元测试A卷——第八章?立体几何初步天津市汇文中学2023-2024学年高一下学期期中考试数学试题【人教A版(2019)】专题15立体几何与空间向量(第四部分)-高一下学期名校期末好题汇编四川省遂宁市射洪中学校2023-2024学年高一下学期期末模拟考试强基班数学试题云南省昭通市威信县第二中学2023-2024学年高二下学期期中考试数学试题
名校
2 . 如图,在四棱锥 中,
中, 平面
平面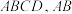

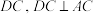 .
.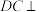 平面
平面 ;
;
(2)若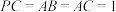 ,求
,求 与平面
与平面 成角的正弦值;
成角的正弦值;
(3)设点 为
为 的中点,过点
的中点,过点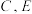 的平面与棱
的平面与棱 交于点
交于点 ,且
,且
 平面
平面 ,求
,求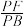 的值.
的值.
 中,
中, 平面
平面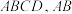

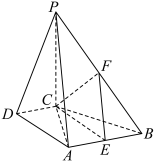
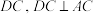 .
.
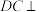 平面
平面 ;
;(2)若
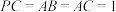 ,求
,求 与平面
与平面 成角的正弦值;
成角的正弦值;(3)设点
 为
为 的中点,过点
的中点,过点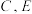 的平面与棱
的平面与棱 交于点
交于点 ,且
,且
 平面
平面 ,求
,求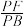 的值.
的值.
您最近一年使用:0次
2024-10-12更新
|
679次组卷
|
3卷引用:辽宁省七校2024-2025学年高二上学期期初考试数学试卷
名校
3 . 如图在四棱锥 中,底面
中,底面 为矩形,侧棱
为矩形,侧棱 ,且
,且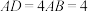 ,
, ,
,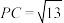 ,点E为AD中点,
,点E为AD中点, 平面
平面 ;
;
(2)求二面角 的余弦值;
的余弦值;
(3)点F为对角线AC上的点,且 ,垂足为G,求FG与平面ABCD所成的最大角的正弦值.
,垂足为G,求FG与平面ABCD所成的最大角的正弦值.
 中,底面
中,底面 为矩形,侧棱
为矩形,侧棱 ,且
,且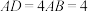 ,
, ,
,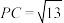 ,点E为AD中点,
,点E为AD中点,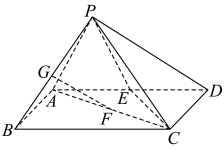
 平面
平面 ;
;(2)求二面角
 的余弦值;
的余弦值;(3)点F为对角线AC上的点,且
 ,垂足为G,求FG与平面ABCD所成的最大角的正弦值.
,垂足为G,求FG与平面ABCD所成的最大角的正弦值.
您最近一年使用:0次
2024-06-23更新
|
860次组卷
|
4卷引用:辽宁省大连市育明高中2023-2024学年高一下学期期末考试数学试卷
辽宁省大连市育明高中2023-2024学年高一下学期期末考试数学试卷浙东北联盟(ZDB)四校2023-2024学年高一下学期期中考试数学试卷(已下线)第3套 全真模拟卷 (中等)【高一期末复习全真模拟】河南省信阳市息县第二高级中学联考2023-2024学年高一下学期7月期末考试数学试题
名校
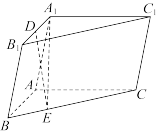
4 . 如图,三棱柱 中,侧面
中,侧面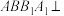 底面
底面 ,
,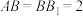 ,
,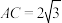 ,
,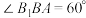 ,点
,点 是棱
是棱 的中点,
的中点, ,
, .
. ;
;
(2)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 中,侧面
中,侧面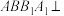 底面
底面 ,
,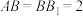 ,
,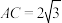 ,
,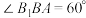 ,点
,点 是棱
是棱 的中点,
的中点, ,
, .
.
 ;
;(2)求直线
 与平面
与平面 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
2024-04-26更新
|
2645次组卷
|
5卷引用:辽宁省锦州市某校2023-2024学年高三下学期考前测试数学试卷(A)
辽宁省锦州市某校2023-2024学年高三下学期考前测试数学试卷(A)湖北省武汉市2024届高三下学期四月调考数学试卷2024届山东省五莲县第一中学高考模拟(二)数学试题河北省张家口市尚义县第一中学等校2024届高三下学期模拟演练数学试题(已下线)专题01 空间向量与立体几何解答题必考题型(6类题型)-备战2023-2024学年高二数学下学期期末真题分类汇编(江苏专用)
名校
5 . 如图,已知四边形 为菱形,四边形
为菱形,四边形 为平行四边形,且
为平行四边形,且 ,
,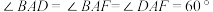 .
. 平面
平面 ;
;
(2)设平面 平面
平面 ,且二面角
,且二面角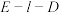 的平面角为
的平面角为 ,
,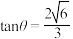 , 设
, 设 为线段
为线段 的中点,求
的中点,求 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 为菱形,四边形
为菱形,四边形 为平行四边形,且
为平行四边形,且 ,
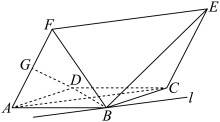
,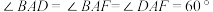 .
.
 平面
平面 ;
;(2)设平面
 平面
平面 ,且二面角
,且二面角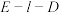 的平面角为
的平面角为 ,
,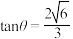 , 设
, 设 为线段
为线段 的中点,求
的中点,求 与平面
与平面 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
2024-07-22更新
|
778次组卷
|
3卷引用:辽宁省大连市育明高中2023-2024学年高一下学期期末考试数学试卷
6 . 如图,在四棱柱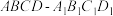 中,平面
中,平面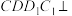 平面
平面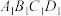 ,
,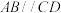 ,
, ,
,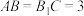 ,
,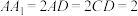 .
. 平面
平面 ;
;
(2)求直线 与平面
与平面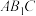 所成角的正弦值.
所成角的正弦值.
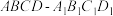 中,平面
中,平面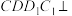 平面
平面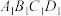 ,
,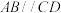 ,
, ,
,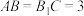 ,
,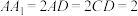 .
.
 平面
平面 ;
;(2)求直线
 与平面
与平面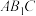 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
2024-07-09更新
|
554次组卷
|
2卷引用:辽宁省辽阳市2023-2024学年高一下学期期末考试数学试卷
2011·河北唐山·一模
名校
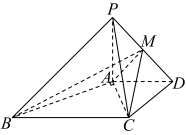
7 . 如图,在四棱锥 中,
中, 平面
平面 ,
,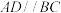 ,
, ,且
,且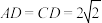 ,
,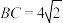 ,
, .
. ;
;
(2)在线段 上,是否存在一点M,使得二面角
上,是否存在一点M,使得二面角 的大小为
的大小为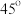 ,如果存在,求
,如果存在,求 与平面
与平面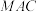 所成角的正弦值,如果不存在,请说明理由.
所成角的正弦值,如果不存在,请说明理由.
 中,
中, 平面
平面 ,
,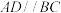 ,
, ,且
,且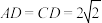 ,
,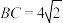 ,
, .
.
 ;
;(2)在线段
 上,是否存在一点M,使得二面角
上,是否存在一点M,使得二面角 的大小为
的大小为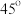 ,如果存在,求
,如果存在,求 与平面
与平面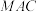 所成角的正弦值,如果不存在,请说明理由.
所成角的正弦值,如果不存在,请说明理由.
您最近一年使用:0次
2023-09-06更新
|
1395次组卷
|
24卷引用:辽宁省大连市第八中学2021-2022学年高二上学期10月阶段考试数学试题
辽宁省大连市第八中学2021-2022学年高二上学期10月阶段考试数学试题(已下线)2011届河北省唐山一中高三高考仿真理数2017届湖南五市十校高三理12月联考数学试卷2018年高考数学(理科,通用版)练酷专题二轮复习课时跟踪检测:(十九) 立体几何河南省南阳市第一中学2018届高三第十四次考试数学(理)试题内蒙古赤峰市2018-2019学年高二下学期期末联考数学(理)试题广东省华南师范大学附属中学2018-2019学年上学期高二年级期末数学试题宁夏六盘山高级中学2020届高三第四次模拟测试数学(理)试题(已下线)专题04 立体几何——2020年高考真题和模拟题理科数学分项汇编人教A版(2019) 选择性必修第一册 过关斩将 第一章 空间向量与立体几何 1.4 空间向量的应用 1.4.2 用空间向量研究距离、夹角问题安徽省池州市第一中学2020-2021学年高二上学期12月月考数学(理)试题江西省吉水中学2020-2021学年高二11月月考数学(理)试题甘肃省民乐县第一中学2021届高三押题卷(二)数学(理)试题(已下线)课时1.4.2 空间向量的应用(02)用空间向量研究距离、夹角问题-2021-2022学年高二数学同步练习和分类专题教案(人教A版2019选择性必修第一册)(已下线)考点52 空间向量在立体几何中的运用-备战2022年高考数学一轮复习考点帮(新高考地区专用)【学科网名师堂】山东省淄博市高青县第一中学2021-2022学年高二上学期10月月考数学试题安徽省六安市舒城中学2022-2023学年高二上学期开学考试数学试题沪教版(2020) 选修第一册 精准辅导 第3章 3.4(4)求角的大小(第2课时)四川省遂宁中学校2022-2023学年高二上学期10月月考数学(理)试题安徽省宣城中学2023-2024学年高二上学期第一次(10月)月考数学试题(已下线)特训02 期末解答题汇编(第1-5章,精选38道)-2023-2024学年高二数学《重难点题型·高分突破》(人教A版2019选择性必修第二册)安徽省合肥市第九中学2023-2024学年高二上学期第一次单元质量检测数学试题(已下线)核心考点8 立体几何中综合问题 B提升卷 (高一期末考试必考的10大核心考点) 云南省大理市大理白族自治州民族中学2024-2025学年高二上学期10月月考数学试题
8 . 如图,在四棱锥 中,底面
中,底面 为菱形,
为菱形,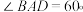 ,
, ,
, 为
为 的中点.
的中点. 平面
平面 ;
;
(2)若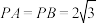 ,
,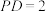 .
.
①求二面角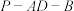 的余弦值;
的余弦值;
②求直线 与平面
与平面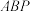 所成角的正弦值.
所成角的正弦值.
 中,底面
中,底面 为菱形,
为菱形,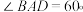 ,
, ,
, 为
为 的中点.
的中点.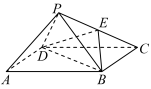
 平面
平面 ;
;(2)若
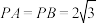 ,
,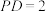 .
.①求二面角
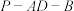 的余弦值;
的余弦值;②求直线
 与平面
与平面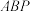 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
2024高三·全国·专题练习
名校
9 . 如图,四面体 中,
中, ,
, ,
, ,
, 为
为 的中点.
的中点.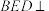 平面
平面 ;
;
(2)设 ,
,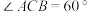 ,点
,点 在
在 上;
上;
①点 为
为 中点,求
中点,求 与
与 所成角的余弦值;
所成角的余弦值;
②当 的面积最小时,求
的面积最小时,求 与平面
与平面 所成的角的正弦值.
所成的角的正弦值.
 中,
中, ,
, ,
, ,
, 为
为 的中点.
的中点.
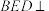 平面
平面 ;
;(2)设
 ,
,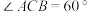 ,点
,点 在
在 上;
上;①点
 为
为 中点,求
中点,求 与
与 所成角的余弦值;
所成角的余弦值;②当
 的面积最小时,求
的面积最小时,求 与平面
与平面 所成的角的正弦值.
所成的角的正弦值.
您最近一年使用:0次
2024-03-18更新
|
1737次组卷
|
5卷引用:辽宁省五校联考2023-2024学年高一下学期期末考试数学试卷
辽宁省五校联考2023-2024学年高一下学期期末考试数学试卷(已下线)第二章 立体几何中的计算 专题一 空间角 微点5 直线与平面所成角综合训练【培优版】山西省临汾市侯马市第一中学校2023-2024学年高一下学期第三次月考数学试题江西省宜春市丰城市第九中学2023-2024学年高一下学期7月期末考试数学试题辽宁省鞍山市第一中学等校2023-2024学年高一下学期7月期末考试数学试题
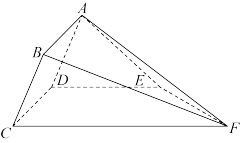
10 . 如图,多面体 中,四边形
中,四边形 为平行四边形,
为平行四边形,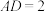 ,
, ,四边形
,四边形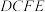 为梯形,
为梯形, ,
, ,
,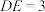 ,
,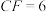 ,
,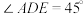 ,平面
,平面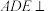 平面
平面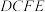 .
.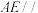 平面
平面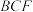 ;
;
(2)求直线 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(3)求点 到平面
到平面 的距离.
的距离.
 中,四边形
中,四边形 为平行四边形,
为平行四边形,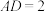 ,
, ,四边形
,四边形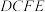 为梯形,
为梯形, ,
, ,
,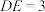 ,
,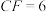 ,
,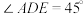 ,平面
,平面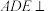 平面
平面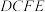 .
.
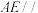 平面
平面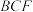 ;
;(2)求直线
 与平面
与平面 所成角的正弦值;
所成角的正弦值;(3)求点
 到平面
到平面 的距离.
的距离.
您最近一年使用:0次
2023-07-18更新
|
911次组卷
|
5卷引用:辽宁省抚顺市第一中学2024-2025学年高二上学期期初考试数学试题
辽宁省抚顺市第一中学2024-2025学年高二上学期期初考试数学试题四川省成都市成都市石室中学2022-2023学年高一下学期期末数学试题四川省眉山市彭山区第一中学2023-2024学年高二上学期开学考试数学试题(已下线)【高一模块二】类型4 以立体几何中的位置关系判断为背景的解答题(B卷提升卷)四川省巴中市恩阳区恩阳中学2024-2025学年高二上学期开学考试数学试卷



