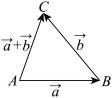
1 . 空间向量的加减运算
| 加法运算 | 三角形法则 | 语言表述 | 首尾顺次相接, |
| 图形表示 |
| ||
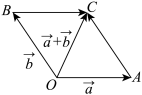
| 平行四边形法则 | 语言表述 | 以共起点的两边为邻边作平行四边形, | |
| 图形表示 |
| ||
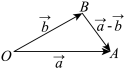
| 减法运算 | 三角形法则 | 语言表述 | 共起点,连终点,方向指向 |
| 图形表示 |
| ||
| 运算律 | 交换律 |  | |
| 结合律 | 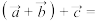 | ||
您最近一年使用:0次
2 . 如何证明加法结合律 ?如图,在平行六面体
?如图,在平行六面体 中,分别标出
中,分别标出 ,
,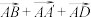 表示的向量.从中你能体会向量加法运算的交换律和结合律吗?一般地,三个不共面的向量的和与这三个向量有什么关系?
表示的向量.从中你能体会向量加法运算的交换律和结合律吗?一般地,三个不共面的向量的和与这三个向量有什么关系?
 ?如图,在平行六面体
?如图,在平行六面体 中,分别标出
中,分别标出 ,
,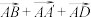 表示的向量.从中你能体会向量加法运算的交换律和结合律吗?一般地,三个不共面的向量的和与这三个向量有什么关系?
表示的向量.从中你能体会向量加法运算的交换律和结合律吗?一般地,三个不共面的向量的和与这三个向量有什么关系?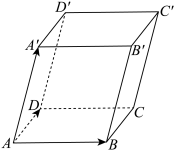
您最近一年使用:0次
3 . 对于空间中的非零向量 ,
,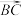 ,
,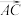 ,其中一定不成立的是( )
,其中一定不成立的是( )
 ,
,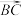 ,
,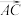 ,其中一定不成立的是( )
,其中一定不成立的是( )A. | B.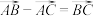 |
C.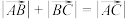 | D.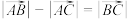 |
您最近一年使用:0次
4 . 已知平行六面体 ,且
,且 ,
,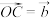 ,
,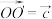 .
.
(1)用 ,
, ,
, 表示向量
表示向量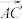 ,并指出它在这组基下的坐标;
,并指出它在这组基下的坐标;
(2)设G,H分别是侧面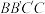 和底面
和底面 的中心,用
的中心,用 ,
, ,
, 表示
表示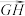 ,并指出它在这组基下的坐标.
,并指出它在这组基下的坐标.
 ,且
,且 ,
,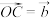 ,
,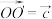 .
.(1)用
 ,
, ,
, 表示向量
表示向量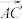 ,并指出它在这组基下的坐标;
,并指出它在这组基下的坐标;(2)设G,H分别是侧面
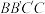 和底面
和底面 的中心,用
的中心,用 ,
, ,
, 表示
表示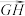 ,并指出它在这组基下的坐标.
,并指出它在这组基下的坐标.
您最近一年使用:0次
5 . 已知空间的一组基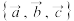 ,
, ,
,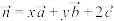 .若向量
.若向量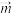 与
与 共线,则
共线,则
__________ ,
__________ .
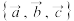 ,
, ,
,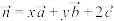 .若向量
.若向量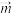 与
与 共线,则
共线,则

您最近一年使用:0次
解题方法
6 . 若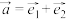 ,
,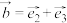 ,
,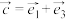 ,
,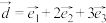 ,若
,若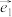 ,
,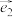 ,
,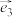 不共面,当
不共面,当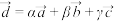 时,
时,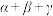 等于( )
等于( )
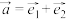 ,
,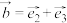 ,
,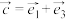 ,
,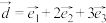 ,若
,若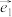 ,
,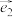 ,
,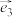 不共面,当
不共面,当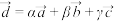 时,
时,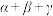 等于( )
等于( )| A.3 | B.5 | C.7 | D.9 |
您最近一年使用:0次
7 . 在空间四边形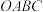 中,若
中,若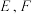 分别是
分别是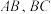 的中点,
的中点, 是
是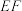 上的点,且
上的点,且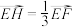 ,记
,记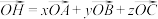 ,则
,则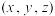 等于( )
等于( )
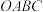 中,若
中,若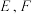 分别是
分别是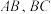 的中点,
的中点, 是
是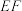 上的点,且
上的点,且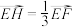 ,记
,记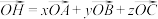 ,则
,则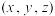 等于( )
等于( )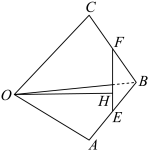
A.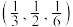 | B.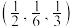 | C. | D.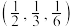 |
您最近一年使用:0次
2024-08-10更新
|
370次组卷
|
3卷引用:【课后练】 2.2.1 空间向量及其线性运算 课后作业-湘教版(2019)选择性必修第二册 第2章 空间向量与立体几何
8 . 下列说法中正确的是( )
| A.空间中共线的向量必在同一条直线上 |
| B.不相等的两个空间向量的模必不相等 |
C.数乘运算中, 既决定大小又决定方向 既决定大小又决定方向 |
D.在四边形ABCD中,一定有 |
您最近一年使用:0次
2024-08-10更新
|
636次组卷
|
3卷引用:【课后练】 2.2.1 空间向量及其线性运算 课后作业-湘教版(2019)选择性必修第二册 第2章 空间向量与立体几何
9 . 已知O,A,B,C,D,E,F,G,H为空间的9个点(如图所示),并且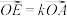 ,
,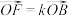 ,
, ,
,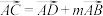 ,
,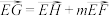 .求证:
.求证:
(2)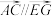 ;
;
(3)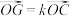 .
.
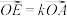 ,
,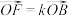 ,
, ,
,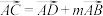 ,
,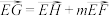 .求证:
.求证: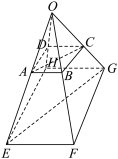
(2)
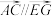 ;
;(3)
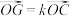 .
.
您最近一年使用:0次
名校
10 . 如图,在平行六面体 中,
中,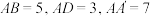 ,
, ,
,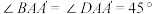 ,则
,则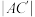 的长为( )
的长为( )
 中,
中,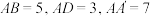 ,
, ,
,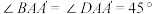 ,则
,则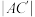 的长为( )
的长为( )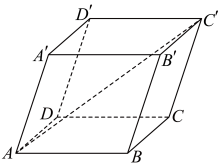
A.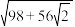 | B.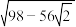 |
C.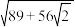 | D. |
您最近一年使用:0次
2024-10-16更新
|
1254次组卷
|
9卷引用:江苏省常州市第一中学2023-2024学年高二下学期4月期中数学试题
江苏省常州市第一中学2023-2024学年高二下学期4月期中数学试题(已下线)第1题 空间向量求线段长度(高二同步9月刊)广东省深圳市建文外国语学校2024-2025学年高二上学期9月月考数学试题(已下线)模块三 较难第1套 模拟卷(高二期中备考模拟)(已下线)核心考点1 空间向量的运算 考点讲解 (高二期中考试必考的核心考点)黑龙江省哈尔滨市第九中学校2024-2025学年高二上学期10月学业阶段性评价考试数学试卷山东省日照实验高级中学2024-2025学年高二上学期阶段性检测数学试卷贵州省黔西南州金成实验学校2024-2025学年高二上学期第一次质量检测数学试卷重庆市北碚区朝阳中学2024-2025学年高二上学期第一次月考数学试题