名校
解题方法
1 . 在空间直角坐标系 中,已知向量
中,已知向量 ,点
,点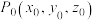 .若直线
.若直线 以
以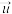 为方向向量且经过点
为方向向量且经过点 ,则直线
,则直线 的标准式方程可表示为
的标准式方程可表示为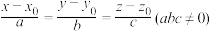 ;若平面
;若平面 以
以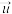 为法向量且经过点
为法向量且经过点 ,则平面
,则平面 的点法式方程可表示为
的点法式方程可表示为 ,一般式方程可表示为
,一般式方程可表示为 .
.
(1)若平面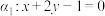 ,平面
,平面 ,直线
,直线 为平面
为平面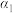 和平面
和平面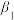 的交线,求直线
的交线,求直线 的单位方向向量(写出一个即可);
的单位方向向量(写出一个即可);
(2)若三棱柱的三个侧面所在平面分别记为 ,其中平面
,其中平面 经过点
经过点 ,
,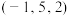 ,平面
,平面 ,平面
,平面 ,求实数m的值;
,求实数m的值;
(3)若集合 ,记集合
,记集合 中所有点构成的几何体为
中所有点构成的几何体为 ,求几何体
,求几何体 的体积和相邻两个面(有公共棱)所成二面角的大小.
的体积和相邻两个面(有公共棱)所成二面角的大小.
 中,已知向量
中,已知向量 ,点
,点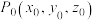 .若直线
.若直线 以
以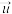 为方向向量且经过点
为方向向量且经过点 ,则直线
,则直线 的标准式方程可表示为
的标准式方程可表示为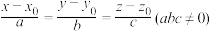 ;若平面
;若平面 以
以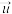 为法向量且经过点
为法向量且经过点 ,则平面
,则平面 的点法式方程可表示为
的点法式方程可表示为 ,一般式方程可表示为
,一般式方程可表示为 .
.(1)若平面
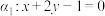 ,平面
,平面 ,直线
,直线 为平面
为平面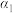 和平面
和平面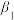 的交线,求直线
的交线,求直线 的单位方向向量(写出一个即可);
的单位方向向量(写出一个即可);(2)若三棱柱的三个侧面所在平面分别记为
 ,其中平面
,其中平面 经过点
经过点 ,
,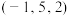 ,平面
,平面 ,平面
,平面 ,求实数m的值;
,求实数m的值;(3)若集合
 ,记集合
,记集合 中所有点构成的几何体为
中所有点构成的几何体为 ,求几何体
,求几何体 的体积和相邻两个面(有公共棱)所成二面角的大小.
的体积和相邻两个面(有公共棱)所成二面角的大小.
您最近一年使用:0次
2024-06-20更新
|
927次组卷
|
11卷引用:福建省部分学校教学联盟2024~2025学年高二上学期入学适应性检测数学试题
福建省部分学校教学联盟2024~2025学年高二上学期入学适应性检测数学试题河南省洛阳市宜阳县部分高中2024-2025学年高二上学期第一次质量检测(9月)数学试题湖北省十堰市竹溪县第二高级中学2024-2025学年高二上学期9月月考数学试卷辽宁省沈阳一二〇中学2024-2025学年高二上学期第一次质量监测数学试题江西省南昌市第十中学2024-2025学年高二上学期第一次月考数学试题黑龙江省大庆市东传高级中学2024-2025学年高二上学期10月月考数学试题广东省惠州市华南师范大学附属惠阳学校2024-2025学年高二上学期第一次月考数学试题辽宁省普通高中2024-2025学年高二上学期11月期中调研测试数学试题(1)广东省东莞市东莞中学2024-2025学年高二上学期第一次段考(10月)数学试卷浙江省宁波市镇海中学2023-2024学年高一下学期期末考试数学试题卷(已下线)专题4 立体几何中的新定义压轴大题(过关集训)
2 . 如图,在棱长为 的正方体
的正方体 中,
中, ,
, ,
, ,
, 分别为棱
分别为棱 ,
, ,
, ,
, 的中点,点
的中点,点 在四边形
在四边形 及其内部运动,
及其内部运动, 是棱
是棱 上的点.当
上的点.当
__________ 时(在线上填入确定的常数),若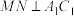 ,则动点
,则动点 的轨迹长为
的轨迹长为__________ (填写一组关系即可).
 的正方体
的正方体 中,
中, ,
, ,
, ,
, 分别为棱
分别为棱 ,
, ,
, ,
, 的中点,点
的中点,点 在四边形
在四边形 及其内部运动,
及其内部运动, 是棱
是棱 上的点.当
上的点.当
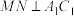 ,则动点
,则动点 的轨迹长为
的轨迹长为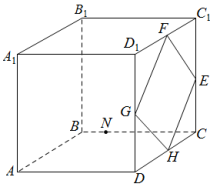
您最近一年使用:0次
2022-03-31更新
|
472次组卷
|
4卷引用:湖北省黄石市有色一中2021-2022学年高二上学期10月月考数学试题
湖北省黄石市有色一中2021-2022学年高二上学期10月月考数学试题(已下线)利用向量法求线面角空间向量与立体几何中的高考新题型(已下线)模块四 专题7 高考新题型(劣构题专训)拔高能力练(人教A)
3 . 已知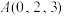 ,
,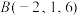 ,
, ,若
,若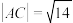 ,则
,则 在
在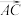 上的投影向量可以是
上的投影向量可以是__________ .(只需写出一个符合题意的答案)
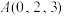 ,
,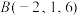 ,
, ,若
,若 ,则
,则 在
在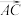 上的投影向量可以是
上的投影向量可以是
您最近一年使用:0次
2023-07-21更新
|
505次组卷
|
8卷引用:浙江省七彩阳光联盟2022-2023学年高二上学期期中数学试题
浙江省七彩阳光联盟2022-2023学年高二上学期期中数学试题福建省厦门第二中学2022-2023学年高二上学期第二次阶段考(12月)数学试题(已下线)专题04 空间直角坐标系及空间运算的坐标表示8种常见考法归类 - 【考点通关】2023-2024学年高二数学高频考点与解题策略(人教A版2019选择性必修第一册)(已下线)专题03 空间向量的坐标与空间直角坐标系5种常见考法归类-【考点通关】2023-2024学年高二数学高频考点与解题策略(人教B版2019选择性必修第一册)(已下线)模块一 专题5《 空间向量运算》 A基础卷(苏教版)【典例题】3.3.2 空间向量的坐标表示 课堂例题-沪教版(2020)选择性必修第一册第3章 空间向量及其应用(已下线)重组5 高二期中真题重组卷(湖北卷)A基础卷(已下线)高考一轮单元复习验收卷·数学(十一)空间向量与立体几何
4 . 在直三棱柱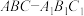 中,
中,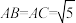 ,
,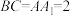 ,点
,点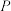 满足
满足 ,其中
,其中 ,
,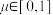 ,则( )
,则( )
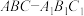 中,
中,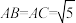 ,
,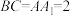 ,点
,点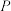 满足
满足 ,其中
,其中 ,
,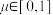 ,则( )
,则( )A.当 时, 时, 的周长为定值 的周长为定值 | B.当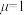 时,三棱锥 时,三棱锥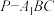 的体积为定值 的体积为定值 |
C.当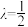 时,使 时,使 的点 的点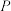 不唯一 不唯一 | D.当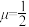 时,有且仅有一个点 时,有且仅有一个点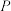 ,使得 ,使得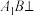 平面 平面 |
您最近一年使用:0次
5 . 已知空间中三点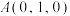 、
、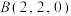 、
、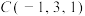 ,则下列结论不正确的有( )
,则下列结论不正确的有( )
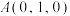 、
、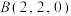 、
、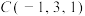 ,则下列结论不正确的有( )
,则下列结论不正确的有( )A. 与 与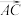 是共线向量 是共线向量 |
B. 的单位向量是 的单位向量是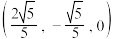 |
C. 与 与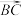 夹角的余弦值是 夹角的余弦值是 |
D.平面 的一个法向量是 的一个法向量是 |
您最近一年使用:0次
2023-10-16更新
|
322次组卷
|
3卷引用:内蒙古自治区赤峰实验中学2023-2024学年高二上学期第一次月考(10月)数学试题
名校
6 . 在下列四个命题中:
①若向量 所在的直线为异面直线,则向量
所在的直线为异面直线,则向量 一定不共面;
一定不共面;
②向量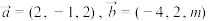 ,若
,若 与
与 的夹角为钝角,则实数m的取值范围为
的夹角为钝角,则实数m的取值范围为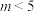 ;
;
③直线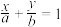 的一个方向向量为
的一个方向向量为 ;
;
④若存在不全为0的实数 使得
使得 ,则
,则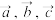 共面.
共面.
其中正确命题的个数是( )
①若向量
 所在的直线为异面直线,则向量
所在的直线为异面直线,则向量 一定不共面;
一定不共面;②向量
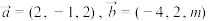 ,若
,若 与
与 的夹角为钝角,则实数m的取值范围为
的夹角为钝角,则实数m的取值范围为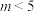 ;
;③直线
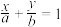 的一个方向向量为
的一个方向向量为 ;
;④若存在不全为0的实数
 使得
使得 ,则
,则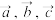 共面.
共面.其中正确命题的个数是( )
| A.0 | B.1 | C.2 | D.3 |
您最近一年使用:0次
2021-12-29更新
|
1096次组卷
|
3卷引用:山东省2021-2022学年高二12月“山东学情”联考数学试题



