23-24高二上·四川成都·期末
名校
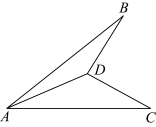
1 . 已知等腰直角三角形ABC, ,点D为BC边上的中点,沿AD折起平面ABD使得
,点D为BC边上的中点,沿AD折起平面ABD使得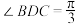 ,则异面直线AB与DC所成角的余弦值为( )
,则异面直线AB与DC所成角的余弦值为( )
 ,点D为BC边上的中点,沿AD折起平面ABD使得
,点D为BC边上的中点,沿AD折起平面ABD使得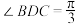 ,则异面直线AB与DC所成角的余弦值为( )
,则异面直线AB与DC所成角的余弦值为( )
A. | B.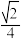 |
C. | D. |
您最近一年使用:0次
2023-12-20更新
|
566次组卷
|
6卷引用:第6章 空间向量与立体几何单元综合测试卷-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)
(已下线)第6章 空间向量与立体几何单元综合测试卷-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)四川省成都市蓉城名校2023-2024学年高二上学期期末联考数学试题四川省绵阳市南山中学实验学校2023-2024学年高二上学期期末模拟数学试题(三)(已下线)四川省绵阳市实验高级中学2023-2024学年高二上学期期末模拟数学试题四川省成都市树德中学2023-2024学年高二下学期入学考试数学试卷四川省绵阳中学2023-2024学年高二下学期入学考试数学试题
23-24高二上·广东佛山·期中
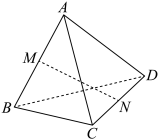
2 . 如图,四面体 的每条棱长都等于
的每条棱长都等于 ,
, 分别是
分别是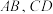 上的动点,则
上的动点,则 的最小值是
的最小值是________ ,此时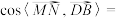
________ .
 的每条棱长都等于
的每条棱长都等于 ,
, 分别是
分别是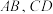 上的动点,则
上的动点,则 的最小值是
的最小值是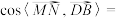
您最近一年使用:0次
23-24高三上·上海虹口·期中
解题方法
3 . 如图所示,在正方体 中,E为线段
中,E为线段 上的动点,则下列直线中与直线CE夹角为定值的直线为( )
上的动点,则下列直线中与直线CE夹角为定值的直线为( )

 中,E为线段
中,E为线段 上的动点,则下列直线中与直线CE夹角为定值的直线为( )
上的动点,则下列直线中与直线CE夹角为定值的直线为( )
A.直线 | B.直线 |
C.直线 | D.直线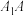 |
您最近一年使用:0次
名校
解题方法
4 . 如图,四棱锥 中,底面
中,底面 是正方形,
是正方形,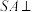 平面
平面 ,
, ,
, 、
、 分别是
分别是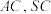 的中点,
的中点, 是棱
是棱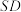 上的动点,则( )
上的动点,则( )
 中,底面
中,底面 是正方形,
是正方形,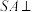 平面
平面 ,
, ,
, 、
、 分别是
分别是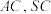 的中点,
的中点, 是棱
是棱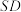 上的动点,则( )
上的动点,则( )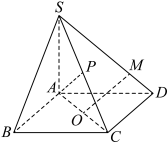
A.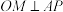 |
B.存在点 ,使 ,使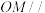 平面 平面 |
C.存在点 ,使直线 ,使直线 与 与 所成的角为 所成的角为 |
D.点 到平面 到平面 与平面 与平面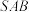 的距离和为定值 的距离和为定值 |
您最近一年使用:0次
2024-04-06更新
|
640次组卷
|
51卷引用:第一章 空间向量与立体几何(B卷·能力提升练)-【单元测试】2022-2023学年高二数学分层训练AB卷(人教B版2019)
第一章 空间向量与立体几何(B卷·能力提升练)-【单元测试】2022-2023学年高二数学分层训练AB卷(人教B版2019)(已下线)第1章 空间向量与立体几何单元测试能力卷-2023-2024学年高二上学期数学人教A版(2019)选择性必修第一册山东省聊城市2021-2022学年高二上学期期末数学试题福建省泉州师范学院附属鹏峰中学2022-2023学年高二上学期8月份统一考试数学试题湖北省孝感市应城市第一高级中学2022-2023学年高二上学期期中数学试题湖南省郴州市2022-2023学年高二上学期期末教学质量监测数学试题江苏省南通市通州高级中学2022-2023学年高二下学期第二次学分检测数学试题安徽省合肥一六八中学2021-2022学年高二上学期第二次月考数学试题江苏省盐城市三校联考2022-2023学年高二下学期第一次学期检测数学试题河南省信阳市商城县上石桥高级中学2023-2024学年高二上学期9月月考数学试题宁夏回族自治区贺兰县第二高级中学2023-2024学年高二上学期第一阶段考试数学试题(已下线)高二数学上学期第一次月考模拟卷01(空间向量与立体几何+直线方程)-【题型分类归纳】2023-2024学年高二数学同步讲与练(人教A版2019选择性必修第一册)重庆市涪陵区部分学校2023-2024学年高二上学期第一次月考数学试题云南省昆明市第三中学2023-2024学年高二上学期第二次综合测试(10月)数学试题山东省烟台市龙口市2023-2024学年高二上学期10月月考数学试题四川省广安第二中学校2023-2024学年高二上学期第一次月考数学试题河南省郑州市第一〇二高级中学2023-2024学年高二上学期10月月考数学试题山东省滕州市第五中学2023-2024学年高二上学期10月月考数学试题广东省东莞实验中学2023-2024学年高二上学期10月月考数学试题广东省东莞市第七高级中学2023-2024学年高二上学期10月月考数学试题山东省青岛市青岛第九中学2023-2024学年高二上学期10月月考数学试题河北省石家庄二十七中2023-2024学年高二上学期第一次月考数学试题安徽省当涂第一中学2023-2024学年高二上学期10月月考数学试题重庆市广益中学校2023-2024学年高二上学期10月月考数学试题河北省石家庄二十三中2023-2024学年高二上学期第一次月考(10月)数学试题吉林省长春市朝阳区长春外国语学校2023-2024学年高二上学期期中数学试题福建省福州十五中、格致鼓山中学、教院二附中、福州铜盘中学、福州十中2023-2024学年高二上学期期中联考数学试题广东省广州市第七十五中学2023-2024学年高二上学期第一次阶段性考试数学试题福建省厦门市国贸协和双语高级中学有限公司2023-2024学年高二上学期11月期中考试数学试题福建省厦门市国贸协和双语高级中学2023-2024学年高二上学期第二次月考数学试题(已下线)第一次月考检测模拟试卷(原卷版)江苏省2023-2024学年高二上学期期末迎考数学试题(R版A卷)湖南省张家界市慈利县第一中学2022-2023学年高二上学期第四次月考数学试题宁夏回族自治区银川市贺兰县第一中学2023-2024学年高二上学期期末复习数学试题(五)(已下线)专题13 空间向量的应用10种常见考法归类(4)河北省石家庄市正定中学2023-2024学年高二上学期期末数学试题江苏省扬州市宝应县氾水高级中学2023-2024学年高二下学期3月阶段调研考试数学试题(已下线)模块五 专题2 全真基础模拟2(苏教版高二期中研习)(已下线)高二 模块3 专题1 第3套 小题进阶提升练(苏教版)江苏省木渎高级中学、苏苑高级中学2022届高三下学期联合适应性检测数学试题福建省莆田第八中学2023届高三上学期入学模拟考试数学试题(一)(已下线)专题08 立体几何综合-备战2023年高考数学母题题源解密(新高考卷)福建省宁德市福安市第一中学2022-2023学年高三上学期第一次检测数学试题江苏省镇江市句容碧桂园学校2022-2023学年高三上学期期初数学试题江苏省宿迁市泗洪县洪翔中学2022-2023学年高三上学期暑期学情检测数学试题江苏省徐州市第七中学2022-2023学年高三上学期9月摸底考试数学试题(已下线)专题8-2 立体几何中的角和距离问题(含探索性问题)-3(已下线)考点17 立体几何中的定值问题 2024届高考数学考点总动员【讲】(已下线)黄金卷03(已下线)模块3 第8套 复盘卷广东省茂名市高州中学2023-2024学年高一下学期期中考试数学试题(创新班1-3班)
22-23高二下·江苏南通·期中
名校
解题方法
5 . 在正三棱柱 中,已知
中,已知 ,
, ,
, 为
为 中点,点
中点,点 在直线
在直线 上,点
上,点 在直线
在直线 上,则( )
上,则( )
 中,已知
中,已知 ,
, ,
, 为
为 中点,点
中点,点 在直线
在直线 上,点
上,点 在直线
在直线 上,则( )
上,则( )A.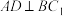 |
B. 平面 平面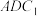 |
C.异面直线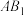 与 与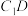 所成角的余弦值为 所成角的余弦值为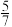 |
D.线段 长度的最小值为 长度的最小值为 |
您最近一年使用:0次
2023-10-16更新
|
323次组卷
|
7卷引用:通关练07 空间向量与立体几何章末检测(二)- 【考点通关】2023-2024学年高二数学高频考点与解题策略(人教A版2019选择性必修第一册)
(已下线)通关练07 空间向量与立体几何章末检测(二)- 【考点通关】2023-2024学年高二数学高频考点与解题策略(人教A版2019选择性必修第一册)江苏省南通市海安市实验中学2022-2023学年高二下学期期中数学试题山东省淄博市临淄中学2023-2024学年高二上学期10月月考数学试题(已下线)广东省佛山市南海区桂城中学2023-2024学年高二上学期第一次段考数学试题辽宁省大连市第八中学2023-2024学年高二上学期10月月考数学试题山东省青岛第五十八中学2023-2024学年高二上学期期中考试数学试卷江苏高二专题02立体几何与空间向量(第二部分)
22-23高二下·福建·期中
解题方法
6 . 在三棱锥 中,
中, ,向量
,向量 与
与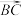 所成角的余弦值是( )
所成角的余弦值是( )
 中,
中, ,向量
,向量 与
与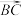 所成角的余弦值是( )
所成角的余弦值是( )A. | B.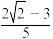 | C.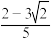 | D.0 |
您最近一年使用:0次
2023-09-28更新
|
424次组卷
|
4卷引用:高二数学上学期期中模拟卷01(前三章:空间向量与立体几何、直线与圆、圆锥曲线)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第一册)
(已下线)高二数学上学期期中模拟卷01(前三章:空间向量与立体几何、直线与圆、圆锥曲线)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第一册)福建省宁德市一级达标校五校联合体2022-2023学年高二下学期期中数学试题(已下线)模块一 专题1 空间向量与立体几何(人教A)2(已下线)高二上期中真题精选(压轴60题30个考点专练)【考题猜想】-2023-2024学年高二数学上学期期中考点大串讲(人教A版2019选择性必修第一册)
22-23高二下·甘肃兰州·期中
名校
解题方法
7 . 四棱锥 的底面是边长为2的菱形,
的底面是边长为2的菱形,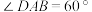 ,对角线AC与BD相交于点O,
,对角线AC与BD相交于点O, 底面ABCD,PB与底面ABCD所成的角为60°,E是PB的中点.
底面ABCD,PB与底面ABCD所成的角为60°,E是PB的中点.
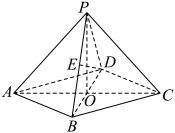
(1)求异面直线DE与PA所成角的余弦值;
(2)证明: 平面PAD,并求点E到平面PAD的距离.
平面PAD,并求点E到平面PAD的距离.
 的底面是边长为2的菱形,
的底面是边长为2的菱形,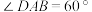 ,对角线AC与BD相交于点O,
,对角线AC与BD相交于点O, 底面ABCD,PB与底面ABCD所成的角为60°,E是PB的中点.
底面ABCD,PB与底面ABCD所成的角为60°,E是PB的中点.
(1)求异面直线DE与PA所成角的余弦值;
(2)证明:
 平面PAD,并求点E到平面PAD的距离.
平面PAD,并求点E到平面PAD的距离.
您最近一年使用:0次
2023-09-10更新
|
3266次组卷
|
13卷引用:高二数学上学期期中模拟卷02(前三章:空间向量与立体几何、直线与圆、圆锥曲线)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第一册)
(已下线)高二数学上学期期中模拟卷02(前三章:空间向量与立体几何、直线与圆、圆锥曲线)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第一册)甘肃省兰州第一中学2022-2023学年高二下学期期中数学试题河北省唐县第一中学2023-2024学年高二上学期第一次考试(9月)数学试题广东省梅州市梅雁中学2023-2024学年高二上学期9月月考数学试题宁夏银川市景博中学2023-2024学年高二上学期9月质量检测数学试题宁夏灵武市第一中学2023-2024学年高二上学期第一次月考数学试题河北省保定市部分高中2023-2024学年高二上学期10月月考数学试题(已下线)模块一 专题1 空间向量与立体几何(人教A)2河北省石家庄二十七中2023-2024学年高二上学期第一次月考数学试题浙江省杭州市富阳区实验中学2023-2024学年高二上学期10月月考数学试题(已下线)专题09 空间距离与角度8种常见考法归类 - 【考点通关】2023-2024学年高二数学高频考点与解题策略(人教B版2019选择性必修第一册)山东省潍坊市高密市第三中学2023-2024学年高三上学期9月月考数学试题湖北省武汉市武钢三中2024届高三下学期开学考试数学试题
22-23高二下·新疆巴音郭楞·期中
8 . 如图,在直三棱柱 中,
中,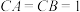 ,
, ,棱
,棱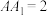 ,
, 、
、 分别为
分别为 、
、 的中点.
的中点.
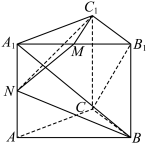
(1)求 与
与 所成角的余弦值;
所成角的余弦值;
(2)求证: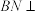 平面
平面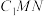 .
.
 中,
中,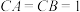 ,
, ,棱
,棱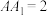 ,
, 、
、 分别为
分别为 、
、 的中点.
的中点.
(1)求
 与
与 所成角的余弦值;
所成角的余弦值;(2)求证:
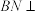 平面
平面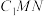 .
.
您最近一年使用:0次
2023-08-27更新
|
570次组卷
|
3卷引用:第3章 空间向量及其应用 单元综合检测(重点)-2023-2024学年高二数学同步精品课堂(沪教版2020选择性必修第一册)
(已下线)第3章 空间向量及其应用 单元综合检测(重点)-2023-2024学年高二数学同步精品课堂(沪教版2020选择性必修第一册)新疆维吾尔自治区巴音郭楞蒙古自治州且末县第一中学2022-2023学年高二下学期期中数学试题(已下线)专题04 空间中的点、直线、平面与空间向量5种常见考法归类 - 【考点通关】2023-2024学年高二数学高频考点与解题策略(人教B版2019选择性必修第一册)
解题方法
9 . 在三棱锥PABC中, 和
和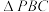 均为等边三角形,且二面角
均为等边三角形,且二面角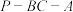 的大小为120°,则异面直线PB和AC所成角的余弦值为
的大小为120°,则异面直线PB和AC所成角的余弦值为________ .
 和
和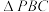 均为等边三角形,且二面角
均为等边三角形,且二面角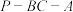 的大小为120°,则异面直线PB和AC所成角的余弦值为
的大小为120°,则异面直线PB和AC所成角的余弦值为
您最近一年使用:0次
22-23高二下·江苏常州·阶段练习
名校
解题方法
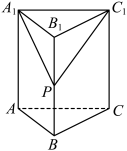
10 . 如图,在正三棱柱 中,
中, ,
,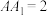 ,P为线段
,P为线段 上的动点,且
上的动点,且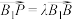 ,则下列命题中正确的是( )
,则下列命题中正确的是( )
 中,
中, ,
,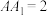 ,P为线段
,P为线段 上的动点,且
上的动点,且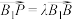 ,则下列命题中正确的是( )
,则下列命题中正确的是( )
A.不存在 使得 使得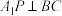 |
B.当 时,三棱柱 时,三棱柱 与三棱锥 与三棱锥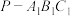 的体积比值为9 的体积比值为9 |
C.当 时,异面直线 时,异面直线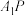 和 和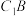 所成角的余弦值为 所成角的余弦值为 |
D.过P且与直线 和直线 和直线 所成角都是 所成角都是 的直线有三条 的直线有三条 |
您最近一年使用:0次
2023-07-24更新
|
640次组卷
|
4卷引用:第一章:空间向量与立体几何章末综合检测卷-【题型分类归纳】2023-2024学年高二数学同步讲与练(人教A版2019选择性必修第一册)
(已下线)第一章:空间向量与立体几何章末综合检测卷-【题型分类归纳】2023-2024学年高二数学同步讲与练(人教A版2019选择性必修第一册)江苏省常州市北郊高级中学2022-2023学年高二下学期5月阶段调研数学试题广东省广州市第八十九中学2023-2024学年高二上学期期中数学试题广东省广州市第六十五中学2023-2024学年高二上学期10月学情检测数学试题



