名校
解题方法
1 . 已知椭圆C: (a>b>0)的两个焦点分别为F1、F2,短轴的一个端点为P.
(a>b>0)的两个焦点分别为F1、F2,短轴的一个端点为P.
(1)若∠F1PF2为直角,焦距长为2,求椭圆C的标准方程;
(2)若∠F1PF2为钝角,求椭圆C的离心率的取值范围.
 (a>b>0)的两个焦点分别为F1、F2,短轴的一个端点为P.
(a>b>0)的两个焦点分别为F1、F2,短轴的一个端点为P.(1)若∠F1PF2为直角,焦距长为2,求椭圆C的标准方程;
(2)若∠F1PF2为钝角,求椭圆C的离心率的取值范围.
您最近一年使用:0次
2020-11-28更新
|
1867次组卷
|
10卷引用:江苏省南通市启东市2020-2021学年高二上学期期中数学试题
江苏省南通市启东市2020-2021学年高二上学期期中数学试题湖南省怀化市雅礼实验学校2022-2023学年高二上学期第一次月考数学试题(已下线)练习7+椭圆-2020-2021学年【补习教材·寒假作业】高二数学(苏教版)黑龙江省齐齐哈尔市讷河市拉哈一中2020-2021学年高二下学期3月月考数学(文)试题江苏省扬州中学2021-2022学年高二上学期10月月考数学试题河北省深州市长江中学2021-2022学年高二上学期12月月考数学试题内蒙古呼伦贝尔市满洲里远方中学2021-2022学年高二下学期期末考试数学(理)试题四川省成都外国语学校2022-2023学年高二上学期期中考试数学(文)试题四川省成都外国语学校2022-2023学年高二上学期期中考试数学(理)试题(已下线)3.1.2 椭圆的简单几何性质【第二练】“上好三节课,做好三套题“高中数学素养晋级之路
名校
解题方法
2 . 已知椭圆E: (
( )的左焦点为
)的左焦点为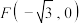 ,过F的直线交E于A、C两点,
,过F的直线交E于A、C两点, 的中点坐标为
的中点坐标为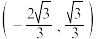 .
.
(1)求椭圆E的方程;
(2)过原点O的直线 和
和 相交且交E于B、D两点,求四边形
相交且交E于B、D两点,求四边形 面积的最大值.
面积的最大值.
 (
( )的左焦点为
)的左焦点为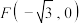 ,过F的直线交E于A、C两点,
,过F的直线交E于A、C两点, 的中点坐标为
的中点坐标为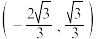 .
.(1)求椭圆E的方程;
(2)过原点O的直线
 和
和 相交且交E于B、D两点,求四边形
相交且交E于B、D两点,求四边形 面积的最大值.
面积的最大值.
您最近一年使用:0次
2020-10-23更新
|
1673次组卷
|
10卷引用:湖南省怀化市2020-2021学年高二上学期10月联考数学试题
湖南省怀化市2020-2021学年高二上学期10月联考数学试题陕西省安康市2020届高三下学期第三次联考理科数学试题(已下线)专题9.7 圆锥曲线综合问题(讲)-2021年新高考数学一轮复习讲练测(已下线)调研测试五(A卷 基础过关检测)-2021年高考数学(理)一轮复习单元滚动双测卷(已下线)专题9.7 圆锥曲线综合问题(精讲)-2021年新高考数学一轮复习学与练(已下线)专题3.1椭圆(B卷提升篇)-2020-2021学年高二数学选择性必修第一册同步单元AB卷(新教材人教A版,浙江专用)陕西省安康市2020届高三下学期第三次教学质量联考文科数学试题陕西省安康市2020届高三下学期第三次教学质量联考理科数学试题广西南宁市第三中学2021届高三下学期开学考试数学(理)试题(已下线)专题9.7 圆锥曲线综合问题 2022年高考数学一轮复习讲练测(新教材新高考)(讲)
名校
解题方法
3 . 已知椭圆 :
: (
( )的两个焦点是
)的两个焦点是 ,
,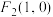 ,且离心率
,且离心率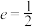 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)过点 作椭圆
作椭圆 的一条切线
的一条切线 交圆
交圆 :
: 于
于 ,
, 两点,求
两点,求 面积的最大值.
面积的最大值.
 :
: (
( )的两个焦点是
)的两个焦点是 ,
,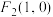 ,且离心率
,且离心率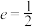 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)过点
 作椭圆
作椭圆 的一条切线
的一条切线 交圆
交圆 :
: 于
于 ,
, 两点,求
两点,求 面积的最大值.
面积的最大值.
您最近一年使用:0次
2020-09-02更新
|
1437次组卷
|
10卷引用:湖南省怀化市2020届高三下学期第二次模拟考试数学(文)试题
湖南省怀化市2020届高三下学期第二次模拟考试数学(文)试题湖南省怀化市2020届高三下学期二模文科数学试题(已下线)考点46 直线与曲线的最值问题(练习)-2021年高考数学复习一轮复习笔记广西钦州市第一中学2021届高三8月月考数学(理)试题广西钦州市第一中学2021届高三9月月考数学(文)试题内蒙古包头市第一中学2020-2021学年高二第一学期期中考试数学(理)试题西藏自治区拉萨中学2021届高三上学期第四次月考数学(文)试题吉林省辽源市友好学校第七十届2020-2021学年高二上学期期末联考数学(理)试题吉林省辽源市友好学校第七十届2020-2021学年高二上学期期末联考数学(文)试题山西省长治市太行中学2020-2021学年高二上学期期末数学(文)试题
4 . 已知椭圆 :
: 的右焦点为
的右焦点为 ,上顶点为
,上顶点为 ,直线
,直线 的斜率为
的斜率为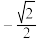 ,且原点到直线
,且原点到直线 的距离为
的距离为 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)若不经过点 的直线
的直线 :
: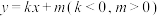 与椭圆
与椭圆 交于
交于 两点,且与圆
两点,且与圆 相切.试探究
相切.试探究 的周长是否为定值,若是,求出定值;若不是,请说明理由.
的周长是否为定值,若是,求出定值;若不是,请说明理由.
 :
: 的右焦点为
的右焦点为 ,上顶点为
,上顶点为 ,直线
,直线 的斜率为
的斜率为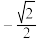 ,且原点到直线
,且原点到直线 的距离为
的距离为 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)若不经过点
 的直线
的直线 :
: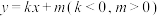 与椭圆
与椭圆 交于
交于 两点,且与圆
两点,且与圆 相切.试探究
相切.试探究 的周长是否为定值,若是,求出定值;若不是,请说明理由.
的周长是否为定值,若是,求出定值;若不是,请说明理由.
您最近一年使用:0次
2020-09-02更新
|
1827次组卷
|
16卷引用:湖南省怀化市2019-2020学年高三上学期期末数学(文)试题
湖南省怀化市2019-2020学年高三上学期期末数学(文)试题湖南省怀化市2019-2020学年高三上学期期末数学(理)试题【省级联考】甘肃、青海、宁夏2019届高三上学期期末联考数学(理)试题【省级联考】甘肃、青海、宁夏2019届高三上学期期末联考数学(文)试题贵州省部分重点中学2019届高三3月联考数学(理)试题【校级联考】贵州省部分重点中学2019届高三3月联考数学(文)试题湖南省湘南教研联盟2019-2020学年高二上学期第二次联考数学试题湖南省2019-2020学年高二上学期12月联考数学试卷陕西省西安中学2020届高三下学期仿真考试(一)数学(理)试题广西南宁三中2019-2020学年下学期高二期末考试(重点班)文科数学试题(已下线)考点45 三定问题(定点、定值、定直线)(练习)-2021年高考数学复习一轮复习笔记广西南宁三中2019-2020学年下学期高二期末考试(重点班)理科数学试题西藏拉萨中学2021届高三上学期第三次月考数学(文)试题(已下线)专题4.2 模拟卷(2)-2022年高考数学大数据精选模拟卷(新高考地区专用)河北省石家庄市第十七中学2022届高三上学期期中数学试题河南省郑州市中牟县2023-2024学年高二上学期期中数学试题
名校
解题方法
5 . 已知椭圆C的中心在坐标原点,焦点在x轴上,它的一个顶点恰好是抛物线 的焦点,离心率为
的焦点,离心率为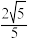 .
.
(1)求椭圆C的标准方程;
(2)过椭圆C的右焦点F作直线l交椭圆C于A、B两点,交y轴于M点,若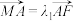 ,
,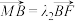 ,求
,求 的值.
的值.
 的焦点,离心率为
的焦点,离心率为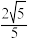 .
.(1)求椭圆C的标准方程;
(2)过椭圆C的右焦点F作直线l交椭圆C于A、B两点,交y轴于M点,若
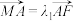 ,
,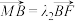 ,求
,求 的值.
的值.
您最近一年使用:0次
2020-08-18更新
|
751次组卷
|
13卷引用:【市级联考】湖南省怀化市2019届高三3月第一次模拟考试数学(文)试题
【市级联考】湖南省怀化市2019届高三3月第一次模拟考试数学(文)试题2019年湖南省怀化市高三一模数学(文)试题2019届湖南省怀化市高三下学期第一次模拟数学(文)试题黑龙江省哈尔滨市宾县一中2019-2020学年高二上学期第一次月考数学(理)试题重庆育才中学2019-2020学年高二第一次月考数学试题2020届陕西省西安中学高三下学期第四次模拟考试数学(文)试题西藏自治区拉萨那曲第二高级中学2019-2020学年高三第二次月考数学(文)试题(已下线)专题21 圆锥曲线综合-2020年高考数学(文)母题题源解密(全国Ⅲ专版)(已下线)专题20 圆锥曲线综合-2020年高考数学(理)母题题源解密(全国Ⅲ专版)江苏省南通市如皋市第一中学2020-2021学年高二上学期9月调研数学试题(已下线)第41讲 解析几何的同构问题-2022年新高考数学二轮专题突破精练黑龙江省八校2021-2022学年高三上学期期末联合考试数学(文)试题(已下线)重难点突破10 圆锥曲线中的向量问题(五大题型)
名校
6 . 以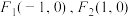 为焦点且与直线
为焦点且与直线 有公共点的椭圆中,离心率最大的椭圆方程是
有公共点的椭圆中,离心率最大的椭圆方程是
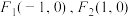 为焦点且与直线
为焦点且与直线 有公共点的椭圆中,离心率最大的椭圆方程是
有公共点的椭圆中,离心率最大的椭圆方程是A.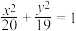 | B. |
C.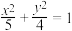 | D. |
您最近一年使用:0次
2020-05-27更新
|
1025次组卷
|
11卷引用:湖南省怀化市辰溪县第一中学2019-2020学年高二上学期12月月考数学试题
湖南省怀化市辰溪县第一中学2019-2020学年高二上学期12月月考数学试题人教B版(2019) 选择性必修第一册 过关斩将 第二章 平面解析几何 2.8 直线与圆锥曲线的位置关系(已下线)第二章 圆锥曲线与方程(能力提升)-2020-2021学年高二数学单元测试定心卷(北师大版选修1-1)(已下线)第三章 圆锥曲线与方程(能力提升)-2020-2021学年高二数学单元测试定心卷(北师大版选修2-1)(已下线)第三课时 课后 3.1.2 第2课时 椭圆的标准方程及性质的应用北师大版(2019) 选修第一册 突围者 第二章 第四节 直线与圆锥曲线的位置关系甘肃省民勤县第一中学2021-2022学年高二上学期第二次月考数学(文)试题2.4.1直线与圆锥曲线的交点 练习-2022-2023学年高二上学期北师大版(2019)选择性必修第一册2.4直线与圆锥曲线的位置关系 综合培优卷-2021-2022学年高二上学期数学北师大版(2019)选择性必修第一册4.1直线与圆锥曲线的交点 同步练习-2022-2023学年高二上学期数学北师大版(2019)选择性必修第一册新疆维吾尔自治区乌鲁木齐市第101中学2024届高三上学期12月月考数学试题
解题方法
7 . 设 、
、 分别是椭圆
分别是椭圆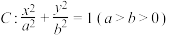 的左、右焦点,
的左、右焦点, 、
、 两点分别是椭圆
两点分别是椭圆 的上、下顶点,
的上、下顶点,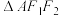 是等腰直角三角形,延长
是等腰直角三角形,延长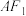 交椭圆
交椭圆 于
于 点,且
点,且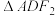 的周长为
的周长为 .
.
(1)求椭圆 的方程;
的方程;
(2)设点 是椭圆
是椭圆 上异于
上异于 、
、 的动点,直线
的动点,直线 、
、 与直线
与直线 分别相交于
分别相交于 、
、 两点,点
两点,点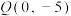 ,试问:
,试问: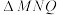 外接圆是否恒过
外接圆是否恒过 轴上的定点(异于点
轴上的定点(异于点 )?若是,求该定点坐标;若否,说明理由.
)?若是,求该定点坐标;若否,说明理由.
 、
、 分别是椭圆
分别是椭圆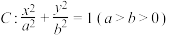 的左、右焦点,
的左、右焦点, 、
、 两点分别是椭圆
两点分别是椭圆 的上、下顶点,
的上、下顶点,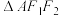 是等腰直角三角形,延长
是等腰直角三角形,延长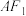 交椭圆
交椭圆 于
于 点,且
点,且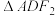 的周长为
的周长为 .
.(1)求椭圆
 的方程;
的方程;(2)设点
 是椭圆
是椭圆 上异于
上异于 、
、 的动点,直线
的动点,直线 、
、 与直线
与直线 分别相交于
分别相交于 、
、 两点,点
两点,点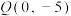 ,试问:
,试问: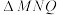 外接圆是否恒过
外接圆是否恒过 轴上的定点(异于点
轴上的定点(异于点 )?若是,求该定点坐标;若否,说明理由.
)?若是,求该定点坐标;若否,说明理由.
您最近一年使用:0次
2020-05-16更新
|
620次组卷
|
4卷引用:湖南省怀化市2020届高三下学期6月第三次模拟考试理科数学试题
湖南省怀化市2020届高三下学期6月第三次模拟考试理科数学试题贵州省普通高等学校招生2019-2020学年高三适应性测试理科数学试题贵州省2019-2020学年高三(4月份)模拟数学(理科)试题(已下线)专题20 圆锥曲线综合-2020年高考数学(理)母题题源解密(全国Ⅲ专版)
解题方法
8 . 已知椭圆 :
: 的左、右焦点分别为
的左、右焦点分别为 、
、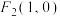 ,椭圆的离心率为
,椭圆的离心率为 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)过点 的直线
的直线 与椭圆
与椭圆 相交于
相交于 ,
, 两点,求
两点,求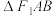 的面积的最大值.
的面积的最大值.
 :
: 的左、右焦点分别为
的左、右焦点分别为 、
、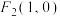 ,椭圆的离心率为
,椭圆的离心率为 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)过点
 的直线
的直线 与椭圆
与椭圆 相交于
相交于 ,
, 两点,求
两点,求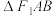 的面积的最大值.
的面积的最大值.
您最近一年使用:0次
9 . 椭圆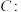
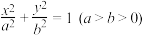 的离心率为
的离心率为 ,其右焦点到点
,其右焦点到点 的距离为
的距离为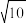 .
.
(1)求椭圆 的方程;
的方程;
(2)若直线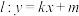 与椭圆
与椭圆 相交于
相交于 ,
, 两点(
两点( ,
, 不是左右顶点),且以
不是左右顶点),且以 为直径的圆过椭圆
为直径的圆过椭圆 的右顶点,求证直线
的右顶点,求证直线 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
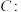
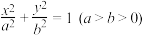 的离心率为
的离心率为 ,其右焦点到点
,其右焦点到点 的距离为
的距离为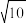 .
.(1)求椭圆
 的方程;
的方程;(2)若直线
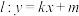 与椭圆
与椭圆 相交于
相交于 ,
, 两点(
两点( ,
, 不是左右顶点),且以
不是左右顶点),且以 为直径的圆过椭圆
为直径的圆过椭圆 的右顶点,求证直线
的右顶点,求证直线 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
您最近一年使用:0次
2020高三·江苏·专题练习
10 . 求满足下列各条件的椭圆的标准方程:
(1)长轴是短轴的3倍且经过点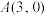 ;
;
(2)短轴一个端点与两焦点组成一个正三角形,且焦点到同侧顶点的距离为 ;
;
(1)长轴是短轴的3倍且经过点
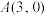 ;
;(2)短轴一个端点与两焦点组成一个正三角形,且焦点到同侧顶点的距离为
 ;
;
您最近一年使用:0次
2020-01-23更新
|
142次组卷
|
3卷引用:专题9.5 椭圆(讲)-江苏版《2020年高考一轮复习讲练测》



