1 . 已知定圆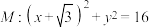 ,动圆N过点
,动圆N过点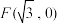 且与圆M相切,记动圆的圆心N的轨迹为E.
且与圆M相切,记动圆的圆心N的轨迹为E.
(1)求轨迹E的方程;
(2)已知两定点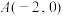 和
和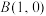 ,过B的动直线
,过B的动直线 交轨迹E于P,Q两点.若直线AP的斜率为
交轨迹E于P,Q两点.若直线AP的斜率为 ,直线AQ的斜率为
,直线AQ的斜率为 ,求证:
,求证: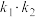 为定值.
为定值.
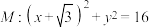 ,动圆N过点
,动圆N过点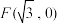 且与圆M相切,记动圆的圆心N的轨迹为E.
且与圆M相切,记动圆的圆心N的轨迹为E.(1)求轨迹E的方程;
(2)已知两定点
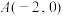 和
和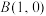 ,过B的动直线
,过B的动直线 交轨迹E于P,Q两点.若直线AP的斜率为
交轨迹E于P,Q两点.若直线AP的斜率为 ,直线AQ的斜率为
,直线AQ的斜率为 ,求证:
,求证: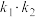 为定值.
为定值.
您最近一年使用:0次
2 . 已知两个定点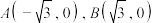 .动点
.动点 满足直线
满足直线 和直线
和直线 的斜率之积是
的斜率之积是
(1)求动点 的轨迹方程,并说明该轨迹是什么曲线;
的轨迹方程,并说明该轨迹是什么曲线;
(2)记(1)中 点的轨迹为曲线
点的轨迹为曲线 ,不经过点
,不经过点 的直线
的直线 与曲线
与曲线 相交于
相交于 两点,且直线
两点,且直线 与直线
与直线 的斜率之积是
的斜率之积是 ,求证:直线
,求证:直线 恒过定点.
恒过定点.
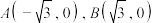 .动点
.动点 满足直线
满足直线 和直线
和直线 的斜率之积是
的斜率之积是
(1)求动点
 的轨迹方程,并说明该轨迹是什么曲线;
的轨迹方程,并说明该轨迹是什么曲线;(2)记(1)中
 点的轨迹为曲线
点的轨迹为曲线 ,不经过点
,不经过点 的直线
的直线 与曲线
与曲线 相交于
相交于 两点,且直线
两点,且直线 与直线
与直线 的斜率之积是
的斜率之积是 ,求证:直线
,求证:直线 恒过定点.
恒过定点.
您最近一年使用:0次
名校
解题方法
3 . 平面内一动点P到直线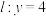 的距离,是它到定点
的距离,是它到定点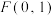 的距离的2倍.
的距离的2倍.
(1)求动点P的轨迹 的方程;
的方程;
(2)经过点F的直线(不与y轴重合)与轨迹 相交于M,N两点,过点M作y轴平行线交直线l于点T,求证:直线
相交于M,N两点,过点M作y轴平行线交直线l于点T,求证:直线 过定点.
过定点.
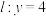 的距离,是它到定点
的距离,是它到定点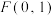 的距离的2倍.
的距离的2倍.(1)求动点P的轨迹
 的方程;
的方程;(2)经过点F的直线(不与y轴重合)与轨迹
 相交于M,N两点,过点M作y轴平行线交直线l于点T,求证:直线
相交于M,N两点,过点M作y轴平行线交直线l于点T,求证:直线 过定点.
过定点.
您最近一年使用:0次
2024-03-29更新
|
451次组卷
|
2卷引用:湖南省邵阳市邵东市第一中学2023-2024学年高二下学期3月月考数学试题
4 . 如图, 为圆
为圆 上一动点,过点
上一动点,过点 分别作
分别作 轴、
轴、 轴的垂线,垂足分别为
轴的垂线,垂足分别为 ,点
,点 满足
满足 ,点
,点 的轨迹记为曲线
的轨迹记为曲线 .
. 的方程;
的方程;
(2)若过点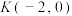 的两条直线
的两条直线 分别交曲线
分别交曲线 于
于 两点,且
两点,且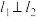 ,求证:直线
,求证:直线 过定点;
过定点;
(3)若曲线 交
交 轴正半轴于点
轴正半轴于点 ,直线
,直线 与曲线
与曲线 交于不同的两点
交于不同的两点 ,直线
,直线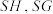 分别交
分别交 轴于
轴于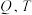 两点,试探究:
两点,试探究: 轴上是否存在点
轴上是否存在点 ,使得
,使得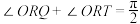 ?若存在,求出点
?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
 为圆
为圆 上一动点,过点
上一动点,过点 分别作
分别作 轴、
轴、 轴的垂线,垂足分别为
轴的垂线,垂足分别为 ,点
,点 满足
满足 ,点
,点 的轨迹记为曲线
的轨迹记为曲线 .
.
 的方程;
的方程;(2)若过点
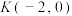 的两条直线
的两条直线 分别交曲线
分别交曲线 于
于 两点,且
两点,且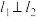 ,求证:直线
,求证:直线 过定点;
过定点;(3)若曲线
 交
交 轴正半轴于点
轴正半轴于点 ,直线
,直线 与曲线
与曲线 交于不同的两点
交于不同的两点 ,直线
,直线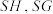 分别交
分别交 轴于
轴于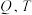 两点,试探究:
两点,试探究: 轴上是否存在点
轴上是否存在点 ,使得
,使得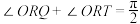 ?若存在,求出点
?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
您最近一年使用:0次
2024-05-29更新
|
391次组卷
|
3卷引用:广东省江门市新会第一中学2024届高三下学期高考热身考试数学试题
23-24高二上·上海浦东新·期中
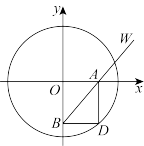
5 . 如图,D为圆O: 上一动点,过点D分别作x轴,y轴的垂线,垂足分别为A,B,连接
上一动点,过点D分别作x轴,y轴的垂线,垂足分别为A,B,连接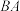 并延长至点W,使得
并延长至点W,使得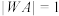 ,点W的轨迹记为曲线
,点W的轨迹记为曲线 .
.
(2)若过点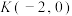 的两条直线
的两条直线 ,
, 分别交曲线C于M,N两点,且
分别交曲线C于M,N两点,且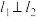 ,求证:直线MN过定点;
,求证:直线MN过定点;
(3)若曲线C交y轴正半轴于点S,直线 与曲线C交于不同的两点G,H,直线SH,SG分别交x轴于P,Q两点.请探究:y轴上是否存在点R,使得
与曲线C交于不同的两点G,H,直线SH,SG分别交x轴于P,Q两点.请探究:y轴上是否存在点R,使得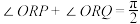 ?若存在,求出点R坐标;若不存在,请说明理由.
?若存在,求出点R坐标;若不存在,请说明理由.
 上一动点,过点D分别作x轴,y轴的垂线,垂足分别为A,B,连接
上一动点,过点D分别作x轴,y轴的垂线,垂足分别为A,B,连接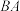 并延长至点W,使得
并延长至点W,使得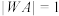 ,点W的轨迹记为曲线
,点W的轨迹记为曲线 .
.
(2)若过点
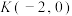 的两条直线
的两条直线 ,
, 分别交曲线C于M,N两点,且
分别交曲线C于M,N两点,且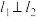 ,求证:直线MN过定点;
,求证:直线MN过定点;(3)若曲线C交y轴正半轴于点S,直线
 与曲线C交于不同的两点G,H,直线SH,SG分别交x轴于P,Q两点.请探究:y轴上是否存在点R,使得
与曲线C交于不同的两点G,H,直线SH,SG分别交x轴于P,Q两点.请探究:y轴上是否存在点R,使得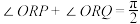 ?若存在,求出点R坐标;若不存在,请说明理由.
?若存在,求出点R坐标;若不存在,请说明理由.
您最近一年使用:0次
2023-11-13更新
|
2614次组卷
|
10卷引用:湖北省荆州市沙市中学2024届高三下学期3月月考数学试题
湖北省荆州市沙市中学2024届高三下学期3月月考数学试题江西省景德镇市乐平中学2023-2024学年高二下学期3月月考数学试题广东省广州市第六中学2023-2024学年高二下学期3月测验数学试题(已下线)上海市华东师范大学第二附属中学2023-2024学年高二上学期期中数学试题江西省吉安市第一中学2024届高三“九省联考”考后适应性测试数学试题(一)(已下线)微考点6-3 圆锥曲线中的定点定值问题(三大题型)湖南省长沙市雅礼实验中学2023-2024学年高二下学期收心检测数学试题(已下线)专题07 直线与圆、圆锥曲线江苏省南京航空航天大学附属高级中学2024届高三下学期期初考试数学试卷河北省邯郸市2024-2025学年高三上学期新高考单科模拟卷(四)(11月期中)数学试题
6 . 已知点 到定点
到定点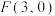 的距离和它到直线
的距离和它到直线 :
: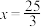 的距离的比是常数
的距离的比是常数 .
.
(1)求点 的轨迹
的轨迹 的方程;
的方程;
(2)若直线 :
: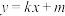 与圆
与圆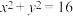 相切,切点
相切,切点 在第四象限,直线
在第四象限,直线 与曲线
与曲线 交于
交于 ,
, 两点,求证:
两点,求证: 的周长为定值.
的周长为定值.
 到定点
到定点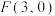 的距离和它到直线
的距离和它到直线 :
: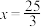 的距离的比是常数
的距离的比是常数 .
.(1)求点
 的轨迹
的轨迹 的方程;
的方程;(2)若直线
 :
: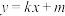 与圆
与圆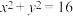 相切,切点
相切,切点 在第四象限,直线
在第四象限,直线 与曲线
与曲线 交于
交于 ,
, 两点,求证:
两点,求证: 的周长为定值.
的周长为定值.
您最近一年使用:0次
2023-09-19更新
|
1165次组卷
|
4卷引用:重庆市2024届高三上学期9月月度质量检测数学试题
重庆市2024届高三上学期9月月度质量检测数学试题云南省大理白族自治州大理市辖区2024届高三区域性规模化统一检测数学试题云南省三校2024届高三高考备考实用性联考卷(三)数学试题(已下线)重难点突破16 圆锥曲线中的定点、定值问题 (十大题型)-1
7 . 在平面直角坐标系xOy中,A,B点的坐标分别为 和
和 ,设
,设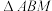 的面积为S,内切圆半径为r,当
的面积为S,内切圆半径为r,当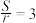 时,记顶点M的轨迹为曲线C.
时,记顶点M的轨迹为曲线C.
(1)求C的方程;
(2)已知点E,F,P,Q在C上,且直线EF与PQ相交于点A,记EF,PQ的斜率分别为 ,
, .
.
(i)设EF的中点为G,PQ的中点为H,证明:存在唯一常数 ,使得当
,使得当 时,
时, ;
;
(ii)若 ,当
,当 最大时,求四边形EPFQ的面积.
最大时,求四边形EPFQ的面积.
 和
和 ,设
,设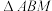 的面积为S,内切圆半径为r,当
的面积为S,内切圆半径为r,当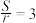 时,记顶点M的轨迹为曲线C.
时,记顶点M的轨迹为曲线C.(1)求C的方程;
(2)已知点E,F,P,Q在C上,且直线EF与PQ相交于点A,记EF,PQ的斜率分别为
 ,
, .
.(i)设EF的中点为G,PQ的中点为H,证明:存在唯一常数
 ,使得当
,使得当 时,
时, ;
;(ii)若
 ,当
,当 最大时,求四边形EPFQ的面积.
最大时,求四边形EPFQ的面积.
您最近一年使用:0次
2024-07-02更新
|
604次组卷
|
7卷引用:广东省深圳实验、湛江一中、珠海一中三校2024届高三上学期12月联考数学试题
广东省深圳实验、湛江一中、珠海一中三校2024届高三上学期12月联考数学试题江苏省苏州市相城区南京师大苏州实验学校2024届高三上学期期末模拟数学试题重庆缙云教育联盟2024届高三高考第一次诊断性检测数学试卷上海市浦东新区上海实验学校2024届高三下学期开学考试数学试题(已下线)第26题 圆锥曲线压轴大题(1)(高三二轮每日一题)河南省信阳市新县高级中学2024届高三考前数学仿真冲刺卷三(已下线)专题5 解析几何中的十一大名圆【练】
名校
解题方法
8 . 在平面直角坐标系中,点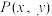 在运动过程中,总满足关系式
在运动过程中,总满足关系式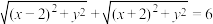 .
.
(1)求点 的轨迹
的轨迹 的方程;
的方程;
(2)过点 作两条斜率分别为
作两条斜率分别为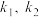 的直线
的直线 和
和 ,分别与
,分别与 交于
交于 和
和 ,线段
,线段 和
和 的中点分别为
的中点分别为 ,若
,若 ,证明直线
,证明直线 过定点.
过定点.
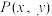 在运动过程中,总满足关系式
在运动过程中,总满足关系式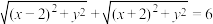 .
.(1)求点
 的轨迹
的轨迹 的方程;
的方程;(2)过点
 作两条斜率分别为
作两条斜率分别为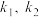 的直线
的直线 和
和 ,分别与
,分别与 交于
交于 和
和 ,线段
,线段 和
和 的中点分别为
的中点分别为 ,若
,若 ,证明直线
,证明直线 过定点.
过定点.
您最近一年使用:0次
2024-07-10更新
|
558次组卷
|
5卷引用:河南省驻马店市新蔡县第一高级中学2023-2024学年高二下学期6月月考数学试题
河南省驻马店市新蔡县第一高级中学2023-2024学年高二下学期6月月考数学试题四川省南充高中2023-2024学年高三下学期第十三次月考理科数学试卷(附答案)四川省南充高中2023-2024学年高三下学期第十三次月考文科数学试卷(附答案)(已下线)模型8 与斜率和有关的定点定值问题模型(已下线)专题10 解析几何中的定点问题(一)【讲】(压轴大全)
名校
解题方法
9 . 已知圆 和点
和点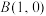 ,点
,点 是圆上任意一点,线段
是圆上任意一点,线段 的垂直平分线与线段
的垂直平分线与线段 相交于点
相交于点 ,记点
,记点 的轨迹为曲线
的轨迹为曲线 .
.
(1)求曲线 的方程;
的方程;
(2)设动直线 与坐标轴不垂直,
与坐标轴不垂直, 与曲线
与曲线 交于不同的
交于不同的 ,
, 两点,且直线
两点,且直线 和
和 的斜率互为相反数.
的斜率互为相反数.
①证明:动直线 恒过
恒过 轴上的某个定点,并求出该定点的坐标;
轴上的某个定点,并求出该定点的坐标;
②求 面积的最大值.
面积的最大值.
 和点
和点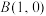 ,点
,点 是圆上任意一点,线段
是圆上任意一点,线段 的垂直平分线与线段
的垂直平分线与线段 相交于点
相交于点 ,记点
,记点 的轨迹为曲线
的轨迹为曲线 .
.(1)求曲线
 的方程;
的方程;(2)设动直线
 与坐标轴不垂直,
与坐标轴不垂直, 与曲线
与曲线 交于不同的
交于不同的 ,
, 两点,且直线
两点,且直线 和
和 的斜率互为相反数.
的斜率互为相反数.①证明:动直线
 恒过
恒过 轴上的某个定点,并求出该定点的坐标;
轴上的某个定点,并求出该定点的坐标;②求
 面积的最大值.
面积的最大值.
您最近一年使用:0次
2024-10-13更新
|
824次组卷
|
2卷引用:湖南省常德市临澧县第一中学2025届高三上学期第二次阶段性考试数学试题
10 . 在直角坐标系 中,已知
中,已知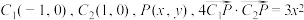 .
.
(1)求点P的轨迹C的方程;
(2)设直线l不过坐标原点且不垂直于坐标轴,l与C交于A、B两点,点 为弦AB的中点.过点M作l的垂线交C于D、E,N为弦DE的中点.
为弦AB的中点.过点M作l的垂线交C于D、E,N为弦DE的中点.
①证明:l与ON相交;
②已知l与直线ON交于T,若 ,求
,求 的最大值.
的最大值.
 中,已知
中,已知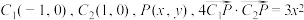 .
.(1)求点P的轨迹C的方程;
(2)设直线l不过坐标原点且不垂直于坐标轴,l与C交于A、B两点,点
 为弦AB的中点.过点M作l的垂线交C于D、E,N为弦DE的中点.
为弦AB的中点.过点M作l的垂线交C于D、E,N为弦DE的中点.①证明:l与ON相交;
②已知l与直线ON交于T,若
 ,求
,求 的最大值.
的最大值.
您最近一年使用:0次



