名校
1 . 已知方程 ,其中
,其中 .现有四位同学对该方程进行了判断,提出了四个命题:
.现有四位同学对该方程进行了判断,提出了四个命题:
甲:可以是圆的方程; 乙:可以是抛物线的方程;
丙:可以是椭圆的标准方程; 丁:可以是双曲线的标准方程.
其中,真命题有( )
 ,其中
,其中 .现有四位同学对该方程进行了判断,提出了四个命题:
.现有四位同学对该方程进行了判断,提出了四个命题:甲:可以是圆的方程; 乙:可以是抛物线的方程;
丙:可以是椭圆的标准方程; 丁:可以是双曲线的标准方程.
其中,真命题有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
您最近一年使用:0次
2023-04-19更新
|
2637次组卷
|
10卷引用:广东省佛山市2023届高三二模数学试题
广东省佛山市2023届高三二模数学试题(已下线)专题01 集合与常用逻辑用语(已下线)专题06 解析几何专题01集合与常用逻辑用语专题17平面解析几何(单选题)(已下线)第05讲 椭圆及其性质(八大题型)(讲义)-1山东省青岛市第五十八中学2024届高三上学期期末数学试题广东省广州市执信中学2024届高三下学期教学情况检测(二)数学试题(已下线)第06讲 双曲线及其性质(十一大题型)(讲义)-1福建省泉州市2023-2024学年高二上学期期末适应性练习数学试题
2 . 设m,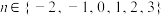 ,曲线C:
,曲线C: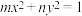 ,则下列说法正确的为( )
,则下列说法正确的为( )
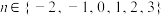 ,曲线C:
,曲线C: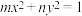 ,则下列说法正确的为( )
,则下列说法正确的为( )A.曲线C表示双曲线的概率为 | B.曲线C表示椭圆的概率为 |
C.曲线C表示圆的概率为 | D.曲线C表示两条直线的概率为 |
您最近一年使用:0次
2023-02-28更新
|
534次组卷
|
4卷引用:陕西省宝鸡市2023届高三二模理科数学试题
陕西省宝鸡市2023届高三二模理科数学试题重庆市缙云教育联盟2023届高三二模数学试题吉林省长春市2023届高三下学期5月四模数学试题(已下线)重难点突破02 概率、统计与其他知识的交汇问题(五大题型)
名校
解题方法
3 . 平面直角坐标系中,动圆T与x轴交于两点A,B,与y轴交于两点C,D,若|AB|和 均为定值,则T的圆心轨迹一定是( )
均为定值,则T的圆心轨迹一定是( )
 均为定值,则T的圆心轨迹一定是( )
均为定值,则T的圆心轨迹一定是( )| A.椭圆(或圆) | B.双曲线 | C.抛物线 | D.前三个答案都不对 |
您最近一年使用:0次
2022-12-14更新
|
1418次组卷
|
7卷引用:云南省通海县第一中学2023届高三上学期11月月考数学试题
云南省通海县第一中学2023届高三上学期11月月考数学试题云南省昆明市第八中学2023届高三下学期2月月考数学试题云南省玉溪市元江哈尼族彝族傣族自治县第一中学2023届高三上学期8月月考数学试题云南省元江哈尼族彝族傣族自治县第一中学2023届高三下学期2月月考数学试题北京市海淀区教师进修学校附属实验学校2022-2023学年高二上学期12月月考数学练习试题新疆生产建设兵团第六师五家渠高级中学2022-2023学年高二下学期开学考试数学试题(已下线)第2章 圆锥曲线(知识归纳+题型突破)-2023-2024学年高二数学单元速记·巧练(沪教版2020选择性必修第一册)
4 . 设非零实数 ,
, 使得曲线
使得曲线 :
: 是双曲线,则( )
是双曲线,则( )
 ,
, 使得曲线
使得曲线 :
: 是双曲线,则( )
是双曲线,则( )A. | B.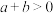 | C.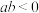 | D. |
您最近一年使用:0次
5 . 平面直角坐标系中有两点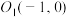 和
和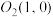 ,以
,以 为圆心,正整数i为半径的圆记为
为圆心,正整数i为半径的圆记为 ,以O2为圆心,正整数j为半径的圆记为
,以O2为圆心,正整数j为半径的圆记为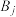 .对于正整数
.对于正整数 (
( ),点
),点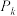 是圆
是圆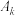 与圆
与圆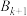 的交点,且
的交点,且 ,
, ,
,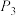 ,
,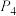 ,
,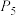 都位于第二象限,则这5个点都在同一( )
都位于第二象限,则这5个点都在同一( )
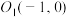 和
和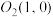 ,以
,以 为圆心,正整数i为半径的圆记为
为圆心,正整数i为半径的圆记为 ,以O2为圆心,正整数j为半径的圆记为
,以O2为圆心,正整数j为半径的圆记为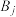 .对于正整数
.对于正整数 (
( ),点
),点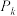 是圆
是圆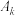 与圆
与圆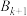 的交点,且
的交点,且 ,
, ,
,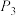 ,
,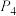 ,
,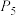 都位于第二象限,则这5个点都在同一( )
都位于第二象限,则这5个点都在同一( )| A.直线上 | B.椭圆上 |
| C.抛物线上 | D.双曲线上 |
您最近一年使用:0次
2022-04-09更新
|
673次组卷
|
5卷引用:广西桂林、崇左、贺州、河池、来宾市2022届高三联合高考模拟考试数学(理)试题
广西桂林、崇左、贺州、河池、来宾市2022届高三联合高考模拟考试数学(理)试题广西桂林、崇左、贺州、河池、来宾市2022届高三联合高考模拟考试数学(文)试题浙江省强基联盟2022届高三下学期5月适应性考试数学试题(已下线)3.2.1 双曲线的标准方程-2022-2023学年高二数学《基础·重点·难点 》全面题型高分突破(苏教版2019选择性必修第一册)(已下线)第12讲 双曲线(5大考点)
6 . 已知函数 ,下列条件,能使得(m,n)的轨迹存在实轴和虚轴相等的双曲线的是( )
,下列条件,能使得(m,n)的轨迹存在实轴和虚轴相等的双曲线的是( )
 ,下列条件,能使得(m,n)的轨迹存在实轴和虚轴相等的双曲线的是( )
,下列条件,能使得(m,n)的轨迹存在实轴和虚轴相等的双曲线的是( )A.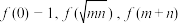 成等差数列 成等差数列 | B.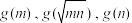 成等比数列 成等比数列 |
C.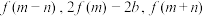 成等差数列 成等差数列 | D.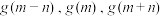 成等比数列 成等比数列 |
您最近一年使用:0次
2021-12-08更新
|
1455次组卷
|
6卷引用:浙江省2022届筑梦九章新高考命题导向研究卷Ⅰ数学试题
浙江省2022届筑梦九章新高考命题导向研究卷Ⅰ数学试题(已下线)专题07 数列的通项与数列的求和(讲)--第一篇 热点、难点突破篇-《2022年高考数学二轮复习讲练测(新高考·全国卷)》(已下线)专题08 数列的通项、求和及综合应用(讲)--第一篇 热点、难点突破篇-《2022年高考数学二轮复习讲练测(浙江专用)》(已下线)热点03 等差数列与等比数列-2022年高考数学【热点·重点·难点】专练(全国通用)(已下线)热点11 圆锥曲线的定义方程与性质【热点·重点·难点】专练(全国通用)(已下线)考向19等差数列及其前n项和(重点)-2



