名校
解题方法
1 . 已知椭圆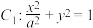 和双曲线
和双曲线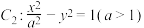 .
.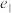 、
、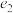 分别为
分别为 和
和 的离心率.
的离心率.
(1)若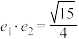 ,求
,求 的渐近线方程;
的渐近线方程;
(2)若 ,过椭圆
,过椭圆 的左焦点
的左焦点 作斜率为
作斜率为 的直线与
的直线与 交于不同两点
交于不同两点 、
、 ,过原点作
,过原点作 的垂线,垂足为
的垂线,垂足为 .若点
.若点 恰好是
恰好是 与
与 的中点,求线段
的中点,求线段 的长度.
的长度.
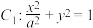 和双曲线
和双曲线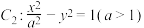 .
.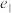 、
、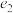 分别为
分别为 和
和 的离心率.
的离心率.(1)若
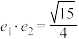 ,求
,求 的渐近线方程;
的渐近线方程;(2)若
 ,过椭圆
,过椭圆 的左焦点
的左焦点 作斜率为
作斜率为 的直线与
的直线与 交于不同两点
交于不同两点 、
、 ,过原点作
,过原点作 的垂线,垂足为
的垂线,垂足为 .若点
.若点 恰好是
恰好是 与
与 的中点,求线段
的中点,求线段 的长度.
的长度.
您最近一年使用:0次
2022-10-29更新
|
600次组卷
|
3卷引用:上海外国语大学附属中学2023届高三上学期9月月考数学试题
解题方法
2 . 已知双曲线 .
.
(1)若离心率为 ,求b的值,
,求b的值, 的顶点坐标、渐近线方程;
的顶点坐标、渐近线方程;
(2)若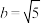 ,是否存在被点
,是否存在被点 平分的弦?如果存在,求弦所在的直线方程;如不存在,请说明理由.
平分的弦?如果存在,求弦所在的直线方程;如不存在,请说明理由.
 .
.(1)若离心率为
 ,求b的值,
,求b的值, 的顶点坐标、渐近线方程;
的顶点坐标、渐近线方程;(2)若
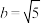 ,是否存在被点
,是否存在被点 平分的弦?如果存在,求弦所在的直线方程;如不存在,请说明理由.
平分的弦?如果存在,求弦所在的直线方程;如不存在,请说明理由.
您最近一年使用:0次
2022-04-26更新
|
471次组卷
|
3卷引用:上海市华东师范大学附属东昌中学2021-2022学年高二下学期期中数学试题
上海市华东师范大学附属东昌中学2021-2022学年高二下学期期中数学试题(已下线)2.3双曲线(作业)(夯实基础+能力提升)-【教材配套课件+作业】2022-2023学年高二数学精品教学课件(沪教版2020选修第一册)【随堂练】2.3.2.1 双曲线的性质 随堂练习-沪教版(2020)选择性必修第一册第2章 圆锥曲线
解题方法
3 . 已知双曲线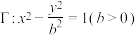 ,直线l与
,直线l与 交于P、Q两点.
交于P、Q两点.
(1)若点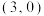 是双曲线
是双曲线 的一个焦点,求
的一个焦点,求 的渐近线方程;
的渐近线方程;
(2)若点P的坐标为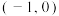 ,直线l的斜率等于1,且
,直线l的斜率等于1,且 ,求双曲线
,求双曲线 的离心率.
的离心率.
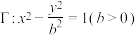 ,直线l与
,直线l与 交于P、Q两点.
交于P、Q两点.(1)若点
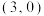 是双曲线
是双曲线 的一个焦点,求
的一个焦点,求 的渐近线方程;
的渐近线方程;(2)若点P的坐标为
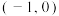 ,直线l的斜率等于1,且
,直线l的斜率等于1,且 ,求双曲线
,求双曲线 的离心率.
的离心率.
您最近一年使用:0次
名校
解题方法
4 . 已知函数 的图像为曲线
的图像为曲线 ,点
,点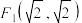 、
、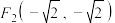 .
.
(1)设点 为曲线
为曲线 上在第一象限内的任意一点,求线段
上在第一象限内的任意一点,求线段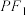 的长(用
的长(用 表示);
表示);
(2)设点 为曲线
为曲线 上任意一点,求证:
上任意一点,求证: 为常数;
为常数;
(3)由(2)可知,曲线 为双曲线,请研究双曲线
为双曲线,请研究双曲线 的性质(从对称性、顶点、渐近线、离心率四个角度进行研究).
的性质(从对称性、顶点、渐近线、离心率四个角度进行研究).
 的图像为曲线
的图像为曲线 ,点
,点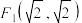 、
、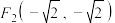 .
.(1)设点
 为曲线
为曲线 上在第一象限内的任意一点,求线段
上在第一象限内的任意一点,求线段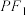 的长(用
的长(用 表示);
表示);(2)设点
 为曲线
为曲线 上任意一点,求证:
上任意一点,求证: 为常数;
为常数;(3)由(2)可知,曲线
 为双曲线,请研究双曲线
为双曲线,请研究双曲线 的性质(从对称性、顶点、渐近线、离心率四个角度进行研究).
的性质(从对称性、顶点、渐近线、离心率四个角度进行研究).
您最近一年使用:0次
2022-01-17更新
|
332次组卷
|
2卷引用:上海交通大学附属中学2021-2022学年高二上学期期末数学试题
解题方法
5 . 已知双曲线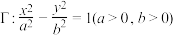 的焦距为
的焦距为 ,渐近线方程为
,渐近线方程为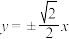 ,
,
(1)求双曲线 的方程;
的方程;
(2)若对任意的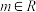 ,直线
,直线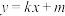 与双曲线
与双曲线 总有公共点,求实数
总有公共点,求实数 的取值范围;
的取值范围;
(3)若过点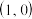 的直线
的直线 与双曲线
与双曲线 交于
交于 两点,问在
两点,问在 轴上是否存在定点
轴上是否存在定点 ,使得
,使得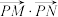 为常数?若存在,求出点
为常数?若存在,求出点 的坐标及此常数的值,若不存在,请说明理由.
的坐标及此常数的值,若不存在,请说明理由.
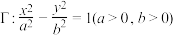 的焦距为
的焦距为 ,渐近线方程为
,渐近线方程为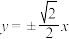 ,
,(1)求双曲线
 的方程;
的方程;(2)若对任意的
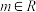 ,直线
,直线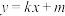 与双曲线
与双曲线 总有公共点,求实数
总有公共点,求实数 的取值范围;
的取值范围;(3)若过点
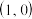 的直线
的直线 与双曲线
与双曲线 交于
交于 两点,问在
两点,问在 轴上是否存在定点
轴上是否存在定点 ,使得
,使得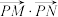 为常数?若存在,求出点
为常数?若存在,求出点 的坐标及此常数的值,若不存在,请说明理由.
的坐标及此常数的值,若不存在,请说明理由.
您最近一年使用:0次
2021-12-24更新
|
1063次组卷
|
4卷引用:上海市松江区2022届高三一模数学试题
上海市松江区2022届高三一模数学试题(已下线)第14讲 双曲线-2(已下线)专题19 圆锥曲线 (模拟练)-22.2双曲线单元检测-2022-2023学年高二上学期数学北师大版(2019)选择性必修第一册
名校
解题方法
6 . 已知椭圆 的离心率与双曲线
的离心率与双曲线 的离心率互为倒数,且椭圆C的焦距、双曲线E的实轴长、双曲线E的焦距依次构成等比数列.
的离心率互为倒数,且椭圆C的焦距、双曲线E的实轴长、双曲线E的焦距依次构成等比数列.
(1)求椭圆C的标准方程;
(2)若双曲线E的虚轴的上端点为 ,问是否存在过点
,问是否存在过点 的直线
的直线 交椭圆C于
交椭圆C于 两点,使得以
两点,使得以 为直径的圆过原点?若存在,求出此时直线
为直径的圆过原点?若存在,求出此时直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
 的离心率与双曲线
的离心率与双曲线 的离心率互为倒数,且椭圆C的焦距、双曲线E的实轴长、双曲线E的焦距依次构成等比数列.
的离心率互为倒数,且椭圆C的焦距、双曲线E的实轴长、双曲线E的焦距依次构成等比数列.(1)求椭圆C的标准方程;
(2)若双曲线E的虚轴的上端点为
 ,问是否存在过点
,问是否存在过点 的直线
的直线 交椭圆C于
交椭圆C于 两点,使得以
两点,使得以 为直径的圆过原点?若存在,求出此时直线
为直径的圆过原点?若存在,求出此时直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
您最近一年使用:0次
2021-08-13更新
|
2422次组卷
|
8卷引用:上海市华东师范大学第三附属中学2021-2022学年高二下学期3月月考数学试题
上海市华东师范大学第三附属中学2021-2022学年高二下学期3月月考数学试题(已下线)专题24 圆锥曲线中的存在性、探索性问题 微点2 圆锥曲线中的探索性问题内蒙古赤峰二中2022-2023学年高二上学期第一次月考(11月)数学(文)试题(已下线)高二下学期第一次月考卷(测试范围:沪教版2020选修一前两章)安徽省淮南一中2020-2021学年高二下学期第二次段考理科数学试题安徽省淮南市淮南第一中学2020-2021学年高二下学期期中数学试题(理)内蒙古赤峰二中2022-2023学年高二下学期第二次月考数学(文)试题四川省成都市石室中学2023届高三适应性模拟检测理科数学试题



