解题方法
1 . 已知双曲线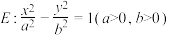 一个顶点为
一个顶点为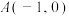 ,直线
,直线 过点
过点 且交双曲线右支于
且交双曲线右支于 两点,记
两点,记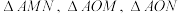 的面积分别为
的面积分别为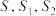 .当
.当 与
与 轴垂直时,
轴垂直时,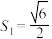
(1)求双曲线 的标准方程;
的标准方程;
(2)若 交
交 轴于点
轴于点 ,
,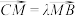 ,
,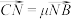 .
.
①求证: 为定值;
为定值;
②若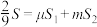 ,当
,当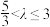 时,求实数
时,求实数 的取值范围.
的取值范围.
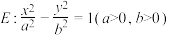 一个顶点为
一个顶点为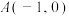 ,直线
,直线 过点
过点 且交双曲线右支于
且交双曲线右支于 两点,记
两点,记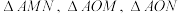 的面积分别为
的面积分别为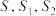 .当
.当 与
与 轴垂直时,
轴垂直时,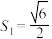
(1)求双曲线
 的标准方程;
的标准方程;(2)若
 交
交 轴于点
轴于点 ,
,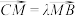 ,
,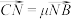 .
.①求证:
 为定值;
为定值;②若
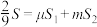 ,当
,当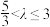 时,求实数
时,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2 . 已知椭圆 的左、右焦点分别为
的左、右焦点分别为 .等轴双曲线
.等轴双曲线 的顶点是
的顶点是 的焦点,焦点是
的焦点,焦点是 的顶点.点
的顶点.点 在
在 上,且位于第一象限,直线
上,且位于第一象限,直线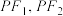 与
与 的交点分别为
的交点分别为 和
和 ,其中
,其中 在
在 轴上方.
轴上方.
(1)求 和
和 的方程;
的方程;
(2)求证: 为定值;
为定值;
(3)设点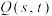 满足直线
满足直线 的斜率为1,记
的斜率为1,记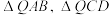 的面积分别为
的面积分别为 .从下面两个条件中选一个,求
.从下面两个条件中选一个,求 的取值范围.
的取值范围.
①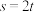 ;②
;② .
.
 的左、右焦点分别为
的左、右焦点分别为 .等轴双曲线
.等轴双曲线 的顶点是
的顶点是 的焦点,焦点是
的焦点,焦点是 的顶点.点
的顶点.点 在
在 上,且位于第一象限,直线
上,且位于第一象限,直线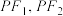 与
与 的交点分别为
的交点分别为 和
和 ,其中
,其中 在
在 轴上方.
轴上方.(1)求
 和
和 的方程;
的方程;(2)求证:
 为定值;
为定值;(3)设点
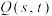 满足直线
满足直线 的斜率为1,记
的斜率为1,记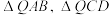 的面积分别为
的面积分别为 .从下面两个条件中选一个,求
.从下面两个条件中选一个,求 的取值范围.
的取值范围.①
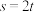 ;②
;② .
.
您最近一年使用:0次
2024-05-30更新
|
436次组卷
|
4卷引用:江苏省徐州市2024届高三高考考前打靶卷数学试题
江苏省徐州市2024届高三高考考前打靶卷数学试题江苏省镇江市扬中市第二高级中学2024届高三下学期高考临门卷数学试题江西省景德镇市昌江区景德镇一中2023-2024学年高二下学期6月期中考试数学试题(已下线)全真综合模拟卷(三)(高三大一轮好卷)(基础卷)
名校
解题方法
3 . 在平面直角坐标系xOy中,已知双曲线C: (
( ,
, )的左、右焦点分别为
)的左、右焦点分别为 、
、 ,
,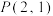 是双曲线C上一点,且
是双曲线C上一点,且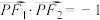 .
.
(1)求双曲线C的方程;
(2)过点P作直线l与双曲线C的两条渐近线分别交于R、S两点.若点P恰为线段RS的中点,求直线l的方程;
(3)设斜率为-2的直线l与双曲线C交于A、B两点,点B关于坐标原点的对称点为D.若直线PA、PD的斜率均存在且分别为 、
、 ,求证:
,求证: 为定值.
为定值.
 (
( ,
, )的左、右焦点分别为
)的左、右焦点分别为 、
、 ,
,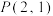 是双曲线C上一点,且
是双曲线C上一点,且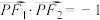 .
.(1)求双曲线C的方程;
(2)过点P作直线l与双曲线C的两条渐近线分别交于R、S两点.若点P恰为线段RS的中点,求直线l的方程;
(3)设斜率为-2的直线l与双曲线C交于A、B两点,点B关于坐标原点的对称点为D.若直线PA、PD的斜率均存在且分别为
 、
、 ,求证:
,求证: 为定值.
为定值.
您最近一年使用:0次
4 . 已知双曲线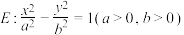 的左顶点为
的左顶点为 ,焦点到渐近线距离为
,焦点到渐近线距离为 .
.
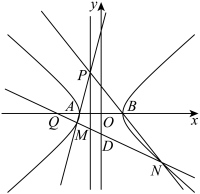
(1)求双曲线E的标准方程;
(2)设双曲线E的右顶点为B,P为直线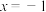 上的动点,连接PA,PB交双曲线于M,N两点(异于A,B),记直线MN与x轴的交点为Q;
上的动点,连接PA,PB交双曲线于M,N两点(异于A,B),记直线MN与x轴的交点为Q;
①求证:Q为定点;
②直线MN交直线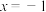 于点D,记
于点D,记 .求证:
.求证: 为定值.
为定值.
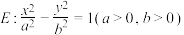 的左顶点为
的左顶点为 ,焦点到渐近线距离为
,焦点到渐近线距离为 .
.
(1)求双曲线E的标准方程;
(2)设双曲线E的右顶点为B,P为直线
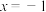 上的动点,连接PA,PB交双曲线于M,N两点(异于A,B),记直线MN与x轴的交点为Q;
上的动点,连接PA,PB交双曲线于M,N两点(异于A,B),记直线MN与x轴的交点为Q;①求证:Q为定点;
②直线MN交直线
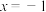 于点D,记
于点D,记 .求证:
.求证: 为定值.
为定值.
您最近一年使用:0次
2023-12-20更新
|
250次组卷
|
2卷引用:江苏省苏州市苏大附中2023-2024学年高二上学期12月月考数学试题
名校
解题方法
5 . 已知双曲线 的离心率为
的离心率为 ,点
,点 在双曲线
在双曲线 上.
上.
(1)求双曲线 的方程;
的方程;
(2)若 为双曲线的左焦点,过点
为双曲线的左焦点,过点 作直线
作直线 交
交 的左支于
的左支于 两点.点
两点.点 ,直线
,直线 交直线
交直线 于点
于点 .设直线
.设直线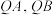 的斜率分别
的斜率分别 ,求证:
,求证: 为定值.
为定值.
 的离心率为
的离心率为 ,点
,点 在双曲线
在双曲线 上.
上.(1)求双曲线
 的方程;
的方程;(2)若
 为双曲线的左焦点,过点
为双曲线的左焦点,过点 作直线
作直线 交
交 的左支于
的左支于 两点.点
两点.点 ,直线
,直线 交直线
交直线 于点
于点 .设直线
.设直线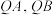 的斜率分别
的斜率分别 ,求证:
,求证: 为定值.
为定值.
您最近一年使用:0次
2023-09-16更新
|
1491次组卷
|
8卷引用:专题12 双曲线的几何性质8种常见考法归类(3)
(已下线)专题12 双曲线的几何性质8种常见考法归类(3)湖南省长沙市周南中学2023-2024学年高三上学期第二次阶段性测试数学试题福建省厦门市厦门大学附属科技中学2024届高三上学期10月月考数学试题(已下线)考点16 解析几何中的定值问题 2024届高考数学考点总动员【练】广西玉林市北流市实验中学等四校2023-2024学年高二上学期期中联考质量评价检测数学试题(已下线)专题07 双曲线的压轴题(5类题型+过关检测)-【常考压轴题】2023-2024学年高二数学上学期压轴题攻略(人教A版2019选择性必修第一册)(已下线)第三章 圆锥曲线的方程(压轴题专练)-2023-2024学年高二数学单元速记·巧练(人教A版2019选择性必修第一册)(已下线)专题25 双曲线的简单几何性质9种常见考法归类(2)
名校
解题方法
6 . 已知双曲线 的一条渐近线方程为
的一条渐近线方程为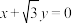 ,虚轴长为2.
,虚轴长为2.
(1)求双曲线 的方程;
的方程;
(2)设直线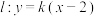 与双曲线
与双曲线 交于
交于 ,
, 两点,点
两点,点 关于
关于 轴的对称点为点
轴的对称点为点 ,求证:直线
,求证:直线 恒过定点.
恒过定点.
 的一条渐近线方程为
的一条渐近线方程为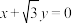 ,虚轴长为2.
,虚轴长为2.(1)求双曲线
 的方程;
的方程;(2)设直线
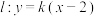 与双曲线
与双曲线 交于
交于 ,
, 两点,点
两点,点 关于
关于 轴的对称点为点
轴的对称点为点 ,求证:直线
,求证:直线 恒过定点.
恒过定点.
您最近一年使用:0次
2023-09-03更新
|
517次组卷
|
3卷引用:江苏省南京市第九中学2023-2024学年高三上学期8月学情检测数学试题
名校
解题方法
7 . 已知双曲线 :
: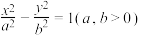 的离心率为
的离心率为 ,直线
,直线 :
: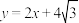 与双曲线C仅有一个公共点.
与双曲线C仅有一个公共点.
(1)求双曲线 的方程
的方程
(2)设双曲线 的左顶点为
的左顶点为 ,直线
,直线 平行于
平行于 ,且交双曲线C于M,N两点,求证:
,且交双曲线C于M,N两点,求证: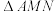 的垂心在双曲线C上.
的垂心在双曲线C上.
 :
: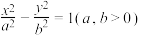 的离心率为
的离心率为 ,直线
,直线 :
: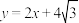 与双曲线C仅有一个公共点.
与双曲线C仅有一个公共点.(1)求双曲线
 的方程
的方程(2)设双曲线
 的左顶点为
的左顶点为 ,直线
,直线 平行于
平行于 ,且交双曲线C于M,N两点,求证:
,且交双曲线C于M,N两点,求证: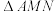 的垂心在双曲线C上.
的垂心在双曲线C上.
您最近一年使用:0次
2023-03-24更新
|
2813次组卷
|
8卷引用:江苏省南京市、盐城市2023届高三下学期一模数学试题
2022高二·江苏·专题练习
解题方法
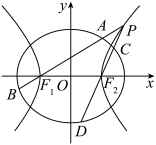
8 . 如图,已知椭圆 的离心率为
的离心率为 ,以该椭圆上的任意一点和椭圆的左、右焦点
,以该椭圆上的任意一点和椭圆的左、右焦点 ,
, 为顶点的三角形的周长为6,双曲线
为顶点的三角形的周长为6,双曲线 的顶点是椭圆
的顶点是椭圆 的焦点,离心率为
的焦点,离心率为 .设
.设 为双曲线
为双曲线 上异于顶点的任一点,直线
上异于顶点的任一点,直线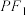 和
和 与椭圆
与椭圆 的交点分别为
的交点分别为 和
和 ,
, .
.
(1)求椭圆 和双曲线
和双曲线 的标准方程;
的标准方程;
(2)设直线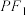 、
、 的斜率分别为
的斜率分别为 、
、 ,求证:
,求证: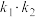 为定值;
为定值;
(3)是否存在常数 ,使得
,使得 恒成立?若存在,求出
恒成立?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 的离心率为
的离心率为 ,以该椭圆上的任意一点和椭圆的左、右焦点
,以该椭圆上的任意一点和椭圆的左、右焦点 ,
, 为顶点的三角形的周长为6,双曲线
为顶点的三角形的周长为6,双曲线 的顶点是椭圆
的顶点是椭圆 的焦点,离心率为
的焦点,离心率为 .设
.设 为双曲线
为双曲线 上异于顶点的任一点,直线
上异于顶点的任一点,直线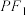 和
和 与椭圆
与椭圆 的交点分别为
的交点分别为 和
和 ,
, .
.
(1)求椭圆
 和双曲线
和双曲线 的标准方程;
的标准方程;(2)设直线
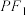 、
、 的斜率分别为
的斜率分别为 、
、 ,求证:
,求证: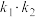 为定值;
为定值;(3)是否存在常数
 ,使得
,使得 恒成立?若存在,求出
恒成立?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
您最近一年使用:0次
名校
解题方法
9 . 三等分角是古希腊几何尺规作图的三大问题之一,如今数学上已经证明三等分任意角是尺规作图不可能问题,如果不局限于尺规,三等分任意角是可能的.下面是数学家帕普斯给出的一种三等分角的方法:已知角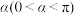 的顶点为
的顶点为 ,在
,在 的两边上截取
的两边上截取 ,连接
,连接 ,在线段
,在线段 上取一点
上取一点 ,使得
,使得 ,记
,记 的中点为
的中点为 ,以
,以 为中心,
为中心, 为顶点作离心率为2的双曲线
为顶点作离心率为2的双曲线 ,以
,以 为圆心,
为圆心, 为半径作圆,与双曲线
为半径作圆,与双曲线 左支交于点
左支交于点 (射线
(射线 在
在 内部),则
内部),则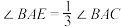 .在上述作法中,以
.在上述作法中,以 为原点,直线
为原点,直线 为
为 轴建立如图所示的平面直角坐标系,若
轴建立如图所示的平面直角坐标系,若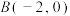 ,点
,点 在
在 轴的上方.
轴的上方. 的方程;
的方程;
(2)若过点 且与
且与 轴垂直的直线交
轴垂直的直线交 轴于点
轴于点 ,点
,点 到直线
到直线 的距离为
的距离为 .
.
证明:①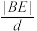 为定值;
为定值;
②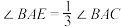 .
.
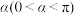 的顶点为
的顶点为 ,在
,在 的两边上截取
的两边上截取 ,连接
,连接 ,在线段
,在线段 上取一点
上取一点 ,使得
,使得 ,记
,记 的中点为
的中点为 ,以
,以 为中心,
为中心, 为顶点作离心率为2的双曲线
为顶点作离心率为2的双曲线 ,以
,以 为圆心,
为圆心, 为半径作圆,与双曲线
为半径作圆,与双曲线 左支交于点
左支交于点 (射线
(射线 在
在 内部),则
内部),则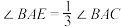 .在上述作法中,以
.在上述作法中,以 为原点,直线
为原点,直线 为
为 轴建立如图所示的平面直角坐标系,若
轴建立如图所示的平面直角坐标系,若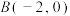 ,点
,点 在
在 轴的上方.
轴的上方.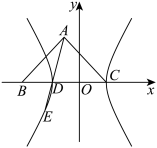
 的方程;
的方程;(2)若过点
 且与
且与 轴垂直的直线交
轴垂直的直线交 轴于点
轴于点 ,点
,点 到直线
到直线 的距离为
的距离为 .
.证明:①
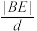 为定值;
为定值;②
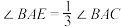 .
.
您最近一年使用:0次
解题方法
10 . 已知双曲线 的两条渐近线分别为
的两条渐近线分别为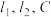 上一点
上一点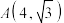 到
到 的距离之积为
的距离之积为 .
.
(1)求双曲线 的方程;
的方程;
(2)设双曲线 的左、右两个顶点分别为
的左、右两个顶点分别为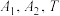 为直线
为直线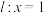 上的动点,且
上的动点,且 不在
不在 轴上,直线
轴上,直线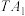 与
与 的另一个交点为
的另一个交点为 ,直线
,直线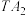 与
与 的另一个交点为
的另一个交点为 ,直线
,直线 与
与 轴的交点为
轴的交点为 ,直线
,直线 与
与 的交点为
的交点为 ,证明
,证明 .
.
 的两条渐近线分别为
的两条渐近线分别为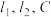 上一点
上一点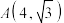 到
到 的距离之积为
的距离之积为 .
.(1)求双曲线
 的方程;
的方程;(2)设双曲线
 的左、右两个顶点分别为
的左、右两个顶点分别为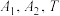 为直线
为直线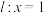 上的动点,且
上的动点,且 不在
不在 轴上,直线
轴上,直线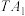 与
与 的另一个交点为
的另一个交点为 ,直线
,直线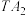 与
与 的另一个交点为
的另一个交点为 ,直线
,直线 与
与 轴的交点为
轴的交点为 ,直线
,直线 与
与 的交点为
的交点为 ,证明
,证明 .
.
您最近一年使用:0次



