1 . 已知椭圆 的右焦点为
的右焦点为 ,斜率不为0的直线
,斜率不为0的直线 与
与 交于
交于 两点.
两点.
(1)若 是线段
是线段 的中点,求直线
的中点,求直线 的方程;
的方程;
(2)若直线 经过点
经过点 (点
(点 在点
在点 之间),直线
之间),直线 与直线
与直线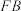 的斜率分别为
的斜率分别为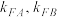 ,求证:
,求证: 为定值.
为定值.
 的右焦点为
的右焦点为 ,斜率不为0的直线
,斜率不为0的直线 与
与 交于
交于 两点.
两点.(1)若
 是线段
是线段 的中点,求直线
的中点,求直线 的方程;
的方程;(2)若直线
 经过点
经过点 (点
(点 在点
在点 之间),直线
之间),直线 与直线
与直线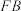 的斜率分别为
的斜率分别为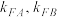 ,求证:
,求证: 为定值.
为定值.
您最近一年使用:0次
2024-10-27更新
|
1867次组卷
|
3卷引用:河南省驻马店市新蔡县第一高级中学2024-2025学年高二上学期10月月考数学试题
解题方法
2 . 已知椭圆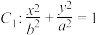 与双曲线
与双曲线 的焦点与
的焦点与 的焦点间的距离为
的焦点间的距离为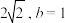 .
.
(1)求 与
与 的方程;
的方程;
(2)过坐标轴上的点 可以作两条
可以作两条 与
与 的公切线.
的公切线.
(i)求点 的坐标.
的坐标.
(ii)当点 在
在 轴上时,是否存在过点
轴上时,是否存在过点 的直线
的直线 ,使
,使 与
与 均有两个交点?若存在,请求出
均有两个交点?若存在,请求出 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
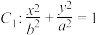 与双曲线
与双曲线 的焦点与
的焦点与 的焦点间的距离为
的焦点间的距离为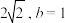 .
.(1)求
 与
与 的方程;
的方程;(2)过坐标轴上的点
 可以作两条
可以作两条 与
与 的公切线.
的公切线.(i)求点
 的坐标.
的坐标.(ii)当点
 在
在 轴上时,是否存在过点
轴上时,是否存在过点 的直线
的直线 ,使
,使 与
与 均有两个交点?若存在,请求出
均有两个交点?若存在,请求出 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
您最近一年使用:0次
2024-10-23更新
|
238次组卷
|
2卷引用:河南省部分重点高中2023-2024学年高三下学期5月考前模拟考试数学试题
解题方法
3 . 已知直线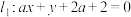 与
与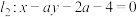 交于点
交于点 .
.
(1)求点 的轨迹方程;
的轨迹方程;
(2)直线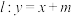 与点
与点 的轨迹交于
的轨迹交于 两点,且以
两点,且以 为直径的圆恰好经过原点,求直线
为直径的圆恰好经过原点,求直线 的方程.
的方程.
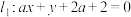 与
与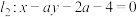 交于点
交于点 .
.(1)求点
 的轨迹方程;
的轨迹方程;(2)直线
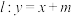 与点
与点 的轨迹交于
的轨迹交于 两点,且以
两点,且以 为直径的圆恰好经过原点,求直线
为直径的圆恰好经过原点,求直线 的方程.
的方程.
您最近一年使用:0次
名校
解题方法
4 . 已知椭圆 的离心率为
的离心率为 ,且过点
,且过点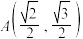 .
.
(1)求椭圆 的方程;
的方程;
(2)直线 与椭圆
与椭圆 交于不同的
交于不同的 ,
, 两点,且直线
两点,且直线 ,
, ,
, 的斜率依次成等比数列.椭圆
的斜率依次成等比数列.椭圆 上是否存在一点
上是否存在一点 ,使得四边形
,使得四边形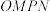 为平行四边形?若存在,求出直线
为平行四边形?若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
 的离心率为
的离心率为 ,且过点
,且过点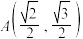 .
.(1)求椭圆
 的方程;
的方程;(2)直线
 与椭圆
与椭圆 交于不同的
交于不同的 ,
, 两点,且直线
两点,且直线 ,
, ,
, 的斜率依次成等比数列.椭圆
的斜率依次成等比数列.椭圆 上是否存在一点
上是否存在一点 ,使得四边形
,使得四边形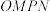 为平行四边形?若存在,求出直线
为平行四边形?若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
您最近一年使用:0次
2024-10-14更新
|
356次组卷
|
9卷引用:河南省周口市沈丘县长安高级中学2022-2023学年高三下学期第二次月考理科数学试题
河南省周口市沈丘县长安高级中学2022-2023学年高三下学期第二次月考理科数学试题四川省南充市嘉陵第一中学2022-2023学年高二下学期第一次月考文科数学试题河北省高碑店市崇德实验中学2023届高三下学期3月月考数学试题广东省深圳外国语学校2022-2023学年高二上学期期末数学试题(已下线)第12讲 第三章 圆锥曲线的方程 章末重点题型大总结(2)(已下线)第04讲 拓展一:直线与椭圆的位置关系-【练透核心考点】2023-2024学年高二数学上学期重点题型方法与技巧(人教A版2019选择性必修第一册)(已下线)专题09 椭圆中定点定值定线四种考法-【常考压轴题】(苏教版2019选择性必修第一册)(已下线)专题4 圆锥曲线中的探究性问题【练】(高二期中压轴专项)(已下线)【实战演练】全真综合模拟卷(二)(高三一轮好卷提升卷)
名校
解题方法
5 . 已知椭圆 的左、右顶点分别为A,B,点
的左、右顶点分别为A,B,点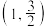 在该椭圆上,且该椭圆的右焦点F的坐标为
在该椭圆上,且该椭圆的右焦点F的坐标为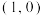 .
.
(2)如图,过点F且斜率为k的直线l与椭圆交于M,N两点,记直线AM的斜率为 ,直线BN的斜率为
,直线BN的斜率为 ,求证:
,求证: .
.
 的左、右顶点分别为A,B,点
的左、右顶点分别为A,B,点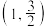 在该椭圆上,且该椭圆的右焦点F的坐标为
在该椭圆上,且该椭圆的右焦点F的坐标为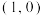 .
.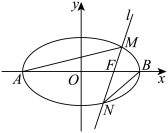
(2)如图,过点F且斜率为k的直线l与椭圆交于M,N两点,记直线AM的斜率为
 ,直线BN的斜率为
,直线BN的斜率为 ,求证:
,求证: .
.
您最近一年使用:0次
2024-09-27更新
|
1361次组卷
|
3卷引用:河南省驻马店市新蔡县第一高级中学2025届高三上学期9月月考数学试题
名校
6 . 已知椭圆 的焦点在
的焦点在 轴上,离心率为
轴上,离心率为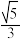 ,对称轴为坐标轴,且经过点
,对称轴为坐标轴,且经过点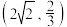 .
.
(1)求椭圆 的方程;
的方程;
(2)若过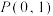 的直线交椭圆
的直线交椭圆 于
于 两点,求
两点,求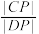 的取值范围.
的取值范围.
 的焦点在
的焦点在 轴上,离心率为
轴上,离心率为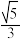 ,对称轴为坐标轴,且经过点
,对称轴为坐标轴,且经过点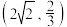 .
.(1)求椭圆
 的方程;
的方程;(2)若过
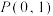 的直线交椭圆
的直线交椭圆 于
于 两点,求
两点,求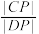 的取值范围.
的取值范围.
您最近一年使用:0次
2024-09-02更新
|
424次组卷
|
4卷引用:河南省郑州外国语学校2025届高三上学期调研考试(五)数学试卷
河南省郑州外国语学校2025届高三上学期调研考试(五)数学试卷 重庆市铜梁一中2025届高三上学期10月月考数学试题河北省2025届高三上学期大数据应用调研联合测评(I)数学试题(已下线)重难点突破06 弦长问题及长度和、差、商、积问题(七大题型)
名校
解题方法
7 . 已知椭圆 的离心率为
的离心率为 ,且过点
,且过点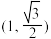 .
.
(1)求椭圆 的方程:
的方程:
(2)过点 的直线
的直线 与椭圆
与椭圆 交于点
交于点 、
、 ,设点
,设点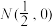 ,若
,若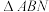 的面积为
的面积为 ,求直线
,求直线 的斜率
的斜率 .
.
 的离心率为
的离心率为 ,且过点
,且过点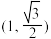 .
.(1)求椭圆
 的方程:
的方程:(2)过点
 的直线
的直线 与椭圆
与椭圆 交于点
交于点 、
、 ,设点
,设点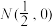 ,若
,若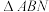 的面积为
的面积为 ,求直线
,求直线 的斜率
的斜率 .
.
您最近一年使用:0次
2024-09-01更新
|
894次组卷
|
3卷引用:河南省南阳市第二中学校2024-2025学年高二上学期10月月考数学试题
名校
8 . 已知椭圆C的两个焦点坐标分别是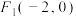 ,
,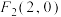 ,且经过点
,且经过点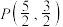 .
.
(1)求C的标准方程;
(2)已知直线l与 平行,且与C有且只有一个公共点,求l的方程.
平行,且与C有且只有一个公共点,求l的方程.
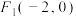 ,
,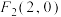 ,且经过点
,且经过点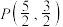 .
.(1)求C的标准方程;
(2)已知直线l与
 平行,且与C有且只有一个公共点,求l的方程.
平行,且与C有且只有一个公共点,求l的方程.
您最近一年使用:0次
2024-08-09更新
|
345次组卷
|
2卷引用:河南省许昌市魏都区许昌高级中学2025届高三上学期8月月考数学试题
名校
解题方法
9 . 已知椭圆C: 的左,右焦点分别为
的左,右焦点分别为 ,
,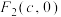 ,过
,过 的直线与椭圆C交于M,N两点,且
的直线与椭圆C交于M,N两点,且 的周长为8,
的周长为8,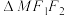 的最大面积为
的最大面积为 .
.
(1)求椭圆C的方程;
(2)设 ,是否存在x轴上的定点P,使得
,是否存在x轴上的定点P,使得 的内心在x轴上,若存在,求出点P的坐标,若不存在,请说明理由.
的内心在x轴上,若存在,求出点P的坐标,若不存在,请说明理由.
 的左,右焦点分别为
的左,右焦点分别为 ,
,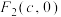 ,过
,过 的直线与椭圆C交于M,N两点,且
的直线与椭圆C交于M,N两点,且 的周长为8,
的周长为8,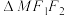 的最大面积为
的最大面积为 .
.(1)求椭圆C的方程;
(2)设
 ,是否存在x轴上的定点P,使得
,是否存在x轴上的定点P,使得 的内心在x轴上,若存在,求出点P的坐标,若不存在,请说明理由.
的内心在x轴上,若存在,求出点P的坐标,若不存在,请说明理由.
您最近一年使用:0次
2024-08-08更新
|
1110次组卷
|
8卷引用:河南省驻马店市新蔡县第一高级中学2024-2025学年高二上学期10月月考数学试卷
河南省驻马店市新蔡县第一高级中学2024-2025学年高二上学期10月月考数学试卷贵州省遵义市正安县第二中学2025届高三上学期第一次月考数学练习试题陕西省榆林市2023-2024学年高三第四次模拟检测数学(理科)试题陕西省榆林市2023-2024学年高三第四次模拟检测文科数学试题(已下线)模型10 圆锥曲线的定点、定值问题模型(第3章 圆锥曲线的方程)(已下线)9.4 点差法与定值、定点和最值(讲义)(已下线)第八章 平面解析几何(测试)(已下线)重难点突破11 圆锥曲线中的探索性与综合性问题(七大题型)
名校
解题方法
10 . 已知椭圆 :
: 的离心率为
的离心率为 ,且经过点
,且经过点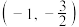 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)过点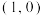 作直线
作直线 与椭圆相交与
与椭圆相交与 ,
, 两点,试问在
两点,试问在 轴上是否存在定点
轴上是否存在定点 ,使得两条不同直线
,使得两条不同直线 ,
,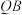 恰好关于
恰好关于 轴对称,若存在,求出点
轴对称,若存在,求出点 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
 :
: 的离心率为
的离心率为 ,且经过点
,且经过点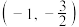 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)过点
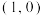 作直线
作直线 与椭圆相交与
与椭圆相交与 ,
, 两点,试问在
两点,试问在 轴上是否存在定点
轴上是否存在定点 ,使得两条不同直线
,使得两条不同直线 ,
,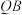 恰好关于
恰好关于 轴对称,若存在,求出点
轴对称,若存在,求出点 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
您最近一年使用:0次
2024-07-20更新
|
683次组卷
|
18卷引用:河南省豫西名校2020-2021学年高二上学期第二次联考数学(文)试题
河南省豫西名校2020-2021学年高二上学期第二次联考数学(文)试题河南省豫西名校2022-2023学年高二上学期第二次联考数学(文)试题山西省朔州市怀仁县大地学校2020-2021学年高二上学期第三次月考文科数学试题山西省朔州市怀仁县大地学校2020-2021学年高二上学期第三次月考理科数学试题山东省临沂第四中学2022-2023学年高二上学期12月份月考数学试题贵州省思南中学2021届高三上学期期中考试数学(文)试题(已下线)【新教材精创】2.8+直线与圆锥曲线的位置关系(2)-A基础练-人教B版高中数学选择性必修第一册(已下线)专题22 圆锥曲线综合——2020年高考数学母题题源解密(山东专版)(已下线)专题22 圆锥曲线综合——2020年高考数学母题题源解密(海南专版)(已下线)专题9.8 《平面解析几何》单元测试卷-2021年新高考数学一轮复习学与练山东省烟台莱阳市第一中学2021-2022学年高二下学期开学摸底考试数学试题(已下线)专题3-4 圆锥曲线定点问题北京市师大附中2022-2023学年高二上学期数学期末试题广东省湛江市第二中学2021-2022学年高二上学期期中考试数学试卷【巩固卷】章末检测试卷(三)单元测试A-湘教版(2019)选择性必修第一册福建省部分学校2025届新高三暑期成果联合质量检测数学试卷北京市北师大附中2022-2023学年高二上学期期末考试数学试题(已下线)重难点突破11 圆锥曲线中的探索性与综合性问题(七大题型)



