名校
解题方法
1 . 已知椭圆C: 的离心率为
的离心率为 ,短轴长为2.
,短轴长为2.
(1)求椭圆C的方程;
(2)设O为坐标原点,F为椭圆C的右焦点,过F的直线l与C交于A,B两点,点M的坐标为 .求证:
.求证: .
.
 的离心率为
的离心率为 ,短轴长为2.
,短轴长为2.(1)求椭圆C的方程;
(2)设O为坐标原点,F为椭圆C的右焦点,过F的直线l与C交于A,B两点,点M的坐标为
 .求证:
.求证: .
.
您最近一年使用:0次
2023-08-17更新
|
1311次组卷
|
6卷引用:江西省南昌市第十中学2022-2023学年高二上学期期中数学试题
江西省南昌市第十中学2022-2023学年高二上学期期中数学试题江西省上饶市余干县蓝天中学2023-2024学年高二上学期期中考试数学试题江西省九江市永修县第一中学2023-2024学年高二上学期10月月考数学试题北京市第十一中学2023-2024学年高二上学期期中练习数学试题(已下线)2.4.2直线与圆锥曲线的综合问题(分层练习)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第一册)(已下线)专题08 椭圆双曲线综合大题(9题型)-【巅峰课堂】2023-2024学年高二数学上学期期中期末复习讲练测(人教A版2019选择性必修第一册)
名校
2 . 如果直线l: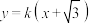 与椭圆C:
与椭圆C: 总有公共点,则实数a的取值范围是
总有公共点,则实数a的取值范围是______ .
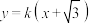 与椭圆C:
与椭圆C: 总有公共点,则实数a的取值范围是
总有公共点,则实数a的取值范围是
您最近一年使用:0次
2023-08-17更新
|
384次组卷
|
4卷引用:江西省南昌市第十中学2022-2023学年高二上学期期中数学试题
江西省南昌市第十中学2022-2023学年高二上学期期中数学试题江西省上饶市余干县蓝天中学2023-2024学年高二上学期期中考试数学试题(已下线)3.1.2 椭圆的简单几何性质(10大题型)精练-【题型分类归纳】2023-2024学年高二数学同步讲与练(人教A版2019选择性必修第一册)(已下线)第3章 圆锥曲线与方程单元检测(基础卷)-2023-2024学年高二数学《重难点题型·高分突破》(苏教版2019选择性必修第一册)
3 . 已知双曲线 :
: 的离心率为
的离心率为 ,其左、右顶点分别为
,其左、右顶点分别为 ,
, ,右焦点为
,右焦点为 ,
, 为
为 的左支上不同于
的左支上不同于 的动点,当
的动点,当 的纵坐标为
的纵坐标为 时,线段
时,线段 的中点恰好在
的中点恰好在 轴上.
轴上.
(1)求双曲线 的标准方程;
的标准方程;
(2)若点 ,连接
,连接 交
交 的右支于点
的右支于点 ,直线
,直线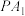 与直线
与直线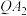 相交于点
相交于点 ,证明:当
,证明:当 在
在 的左支上运动时,点
的左支上运动时,点 在定直线上.
在定直线上.
 :
: 的离心率为
的离心率为 ,其左、右顶点分别为
,其左、右顶点分别为 ,
, ,右焦点为
,右焦点为 ,
, 为
为 的左支上不同于
的左支上不同于 的动点,当
的动点,当 的纵坐标为
的纵坐标为 时,线段
时,线段 的中点恰好在
的中点恰好在 轴上.
轴上.(1)求双曲线
 的标准方程;
的标准方程;(2)若点
 ,连接
,连接 交
交 的右支于点
的右支于点 ,直线
,直线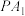 与直线
与直线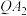 相交于点
相交于点 ,证明:当
,证明:当 在
在 的左支上运动时,点
的左支上运动时,点 在定直线上.
在定直线上.
您最近一年使用:0次
名校
解题方法
4 . 已知椭圆 的离心率为
的离心率为 ,且过点
,且过点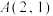
(1)求椭圆C的标准方程;
(2)若直线l交C于P,Q两点,直线 的斜率之和为0,求直线l的斜率
的斜率之和为0,求直线l的斜率
 的离心率为
的离心率为 ,且过点
,且过点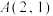
(1)求椭圆C的标准方程;
(2)若直线l交C于P,Q两点,直线
 的斜率之和为0,求直线l的斜率
的斜率之和为0,求直线l的斜率
您最近一年使用:0次
2022-10-15更新
|
1154次组卷
|
2卷引用:江西省赣州市十校协作2022-2023学年高二上学期期中联考数学试题
名校
解题方法
5 . 已知椭圆 的一个焦点与短轴的一个端点连线的倾斜角为
的一个焦点与短轴的一个端点连线的倾斜角为 ,直线
,直线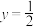 与椭圆
与椭圆 相交于
相交于 和
和 两点,且
两点,且 为坐标原点.
为坐标原点.
(1)求椭圆 的方程;
的方程;
(2)直线 与椭圆
与椭圆 交于
交于 两点,直线
两点,直线 的斜率为
的斜率为 ,直线
,直线 的斜率为
的斜率为 ,且
,且 ,求
,求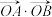 的取值范围.
的取值范围.
 的一个焦点与短轴的一个端点连线的倾斜角为
的一个焦点与短轴的一个端点连线的倾斜角为 ,直线
,直线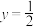 与椭圆
与椭圆 相交于
相交于 和
和 两点,且
两点,且 为坐标原点.
为坐标原点.(1)求椭圆
 的方程;
的方程;(2)直线
 与椭圆
与椭圆 交于
交于 两点,直线
两点,直线 的斜率为
的斜率为 ,直线
,直线 的斜率为
的斜率为 ,且
,且 ,求
,求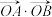 的取值范围.
的取值范围.
您最近一年使用:0次
2022-07-13更新
|
795次组卷
|
5卷引用:江西省吉安市第一中学2022-2023学年高三上学期11月期中考试理科数学试题
名校
6 . 已知椭圆 ,四点
,四点 中恰有三点在椭圆C上.点P为圆
中恰有三点在椭圆C上.点P为圆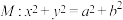 上任意一点,O为坐标原点.
上任意一点,O为坐标原点.
(1)求椭圆C及圆M的标准方程;
(2)设直线l经过点P,且与椭圆C相切,与圆M相交于另一点A,点A关于原点的对称点为B,试判断直线 与椭圆C的位置关系,并证明你的结论.
与椭圆C的位置关系,并证明你的结论.
 ,四点
,四点 中恰有三点在椭圆C上.点P为圆
中恰有三点在椭圆C上.点P为圆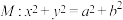 上任意一点,O为坐标原点.
上任意一点,O为坐标原点.(1)求椭圆C及圆M的标准方程;
(2)设直线l经过点P,且与椭圆C相切,与圆M相交于另一点A,点A关于原点的对称点为B,试判断直线
 与椭圆C的位置关系,并证明你的结论.
与椭圆C的位置关系,并证明你的结论.
您最近一年使用:0次
21-22高二·全国·课后作业
名校
解题方法
7 . 已知经过椭圆C: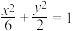 的焦点且与长轴垂直的直线l与椭圆C交于M,N两点,求
的焦点且与长轴垂直的直线l与椭圆C交于M,N两点,求 的面积.
的面积.
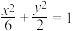 的焦点且与长轴垂直的直线l与椭圆C交于M,N两点,求
的焦点且与长轴垂直的直线l与椭圆C交于M,N两点,求 的面积.
的面积.
您最近一年使用:0次
2022-03-06更新
|
2657次组卷
|
5卷引用:江西省上饶市广丰区重点高中2022-2023学年高二上学期期中考试数学试题
8 . 已知椭圆 一个顶点
一个顶点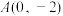 ,以椭圆
,以椭圆 的四个顶点为顶点的四边形面积为
的四个顶点为顶点的四边形面积为 .
.
(1)求椭圆E的方程;
(2)过点P(0,-3)的直线l斜率为k的直线与椭圆E交于不同的两点B,C,直线AB,AC分别与直线 交于点M,N,当|PM|+|PN|≤15时,求k的取值范围.
交于点M,N,当|PM|+|PN|≤15时,求k的取值范围.
 一个顶点
一个顶点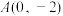 ,以椭圆
,以椭圆 的四个顶点为顶点的四边形面积为
的四个顶点为顶点的四边形面积为 .
.(1)求椭圆E的方程;
(2)过点P(0,-3)的直线l斜率为k的直线与椭圆E交于不同的两点B,C,直线AB,AC分别与直线
 交于点M,N,当|PM|+|PN|≤15时,求k的取值范围.
交于点M,N,当|PM|+|PN|≤15时,求k的取值范围.
您最近一年使用:0次
2021-06-17更新
|
29195次组卷
|
79卷引用:江西省上饶市广丰区重点高中2022-2023学年高二上学期期中考试数学试题
江西省上饶市广丰区重点高中2022-2023学年高二上学期期中考试数学试题新疆维吾尔自治区喀什地区疏勒县实验学校2022-2023学年高三上学期期中数学试题(理科)(已下线)考点39 曲线与方程-备战2022年高考数学一轮复习考点帮(浙江专用)(已下线)考点25 圆锥曲线-备战2022年高考数学(文)一轮复习考点微专题(已下线)专题05 平面解析几何-2021年高考真题和模拟题数学(理)专项汇编(全国通用)(已下线)专题9.7 圆锥曲线综合问题 2022年高考数学一轮复习讲练测(新教材新高考)(讲)(已下线)考向40 椭圆(已下线)专题13圆锥曲线范围最值问题(讲)(文科)第一篇 热点、难点突破篇-《2022年高考文科数学二轮复习讲练测》(全国课标版)(已下线)专题13圆锥曲线范围最值问题(练)(文科)第一篇 热点、难点突破篇-《2022年高考文科数学二轮复习讲练测》(全国课标版)(已下线)专题13圆锥曲线范围最值问题(练)(理科)第一篇 热点、难点突破篇-《2022年高考理科数学二轮复习讲练测》(全国课标版)(已下线)专题13圆锥曲线范围最值问题(讲)(理科)第一篇 热点、难点突破篇-《2022年高考理科数学二轮复习讲练测》(全国课标版)(已下线)第42讲 解析几何中的长度之和差积商平方问题-2022年新高考数学二轮专题突破精练(已下线)第4讲 圆锥曲线中的最值、范围、存在性问题(讲)-2022年高考数学二轮复习讲练测(新教材·新高考地区专用)(已下线)专题13 解析几何中的范围、最值和探索性问题(讲)--第一篇 热点、难点突破篇-《2022年高考数学二轮复习讲练测(浙江专用)》(已下线)专题14 解析几何中的范围、最值和探索性问题(讲)--第一篇 热点、难点突破篇-《2022年高考数学二轮复习讲练测(新高考·全国卷)》(已下线)专题44 巧求圆锥曲线中的最值和范围问题-学会解题之高三数学万能解题模板【2022版】(已下线)专题10.6—圆锥曲线—椭圆大题(取值范围问题)—2022届高三数学一轮复习精讲精练(已下线)思想03 数形结合思想(讲)--第三篇 思想方法篇-《2022年高考数学二轮复习讲练测(浙江专用)》(已下线)思想03 数形结合思想(讲)--第三篇 思想方法篇-《2022年高考数学二轮复习讲练测(新高考·全国卷)》(已下线)专题26 圆锥曲线(理科)解答题20题-备战2022年高考数学冲刺横向强化精练精讲(已下线)专题46 盘点圆锥曲线中的最值与范围问题——备战2022年高考数学二轮复习常考点专题突破(已下线)热点12 圆锥曲线中综合问题-2022年高考数学【热点·重点·难点】专练(全国通用)(已下线)专题22圆锥曲线解答题20题-备战2022年高考数学冲刺横向强化精练精讲(新高考专用)(已下线)押新高考第21题 圆锥曲线-备战2022年高考数学临考题号押题(新高考专用)(已下线)解密14 圆锥曲线(讲义)-【高频考点解密】2022年高考数学二轮复习讲义+分层训练(浙江专用)(已下线)2022年高考考前20天终极冲刺攻略(三)【数学】(新高考地区专用)(5月29日)安徽省合肥市第八中学2022届高三下学期最后一卷保温理科数学试题(已下线)专题6 圆锥曲线硬解定理 微点1 圆锥曲线硬解定理天津市耀华中学2022届高三下学期统练10数学试题湘教版(2019) 选修第一册 突围者 第3章 章末培优专练2023版 苏教版(2019) 选修第一册 突围者 第3章 章末培优专练2023版 北师大版(2019) 选修第一册 名师精选卷 第二章 圆锥曲线2023版 苏教版(2019) 选修第一册 名师精选卷 第三章 圆锥曲线与方程北京市第八中学2023届高三上学期8月测试二数学试题(已下线)专题23 圆锥曲线中的最值、范围问题 微点2 圆锥曲线中的范围问题江苏省盐城市响水中学2022-2023学年高二上学期10月学情分析考试数学试题山西省运城市景胜中学2022-2023学年高二上学期11月月考数学(A)试题吉林省长春市绿园区长春市十一高中2022-2023学年高三上学期10月月考数学试题江西省抚州市第一中学2022-2023学年高二下学期第一次月考数学试题黑龙江省哈尔滨师范大学附属中学2021-2022学年高二上学期期末数学试题2021年北京市高考数学试题河北省衡水市第一中学2022届高三上学期第一次调研数学试题(已下线)考点43 直线与圆锥曲线的位置关系-备战2022年高考数学(理)一轮复习考点帮(已下线)考点40 椭圆-备战2022年高考数学(理)一轮复习考点帮(已下线)考点38 椭圆-备战2022年高考数学(文)一轮复习考点帮(已下线)考点41 直线与圆锥曲线的位置关系-备战2022年高考数学(文)一轮复习考点帮(已下线)专题05 平面解析几何-2021年高考真题和模拟题数学(文)分项汇编(全国通用)北京市第八中学2022届高三10月月考练习数学试题广东省阳春市第一中学2022届高三上学期10月月考数学试题(已下线)第42讲 椭圆(讲) — 2022年高考数学一轮复习讲练测(课标全国版)(已下线)2021年新高考北京数学高考真题变式题16-21题四川省双流中学2021-2022学年高三上学期11月月考数学(理)试题上海市黄浦区大同中学2022届高三上学期12月月考数学试题(已下线)专题29 《圆锥曲线与方程》中的高考真题训练-2021-2022学年高二数学同步培优训练系列(苏教版2019选择性必修第一册) (已下线)专题11圆锥曲线的方程与性质(测)(文科)第一篇 热点、难点突破篇-《2022年高考文科数学二轮复习讲练测》(全国课标版)(已下线)专题11圆锥曲线的方程与性质(测)(理科)第一篇 热点、难点突破篇-《2022年高考理科数学二轮复习讲练测》(全国课标版)安徽省芜湖市第一中学2021-2022学年高二上学期第二次月考数学试题天津市滨海新区塘沽第一中学2023届高三上学期线上统练摸底考试数学试题沪教版(2020) 25天高考冲刺 双新双基百分百25湖北省高中名校联合体2022-2023学年高三下学期开学诊断性考试数学试题(已下线)专题8 解析几何 第3讲 圆锥曲线中的最值、范围、证明问题(已下线)重组卷01(已下线)重组卷03(已下线)专题8-2 圆锥曲线综合大题归类(讲+练)-1安徽省亳州市蒙城第一中学2023届高三下学期最后一卷(三模)数学试题云南省临沧市民族中学2022-2023学年高二下学期第三次月考数学试题(已下线)北京十年真题专题08平面解析几何北京十年真题专题08平面解析几何北京市第一六六中学2024届高三上学期9月阶段性诊断数学试题新疆阿克苏地区柯坪县柯坪湖州国庆中学2024届高三上学期9月月考数学试题(已下线)第6讲:最值范围问题【练】(已下线)专题08 圆锥曲线 第一讲 圆锥曲线的方程与性质(分层练)(已下线)专题24 解析几何解答题(文科)-1(已下线)专题24 解析几何解答题(理科)-1专题12平面解析几何(第二部分)(已下线)五年北京专题08平面解析几何(已下线)专题7 圆锥曲线硬解定理【讲】(已下线)专题9 圆锥曲线中的范围、最值问题(二)【讲】(压轴大全)单元测试B卷——第三章 圆锥曲线的方程
名校
解题方法
9 . 已知椭圆C: (a>b>0)的焦点坐标分别为F1(-1,0),F2(1,0),P为椭圆C上一点,满足3|PF1|=5|PF2|且cos∠F1PF2=
(a>b>0)的焦点坐标分别为F1(-1,0),F2(1,0),P为椭圆C上一点,满足3|PF1|=5|PF2|且cos∠F1PF2= .
.
(1)求椭圆C的标准方程;
(2)设直线l:y=kx+m与椭圆C交于A,B两点,点Q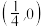 ,若|AQ|=|BQ|,求k的取值范围.
,若|AQ|=|BQ|,求k的取值范围.
 (a>b>0)的焦点坐标分别为F1(-1,0),F2(1,0),P为椭圆C上一点,满足3|PF1|=5|PF2|且cos∠F1PF2=
(a>b>0)的焦点坐标分别为F1(-1,0),F2(1,0),P为椭圆C上一点,满足3|PF1|=5|PF2|且cos∠F1PF2= .
.(1)求椭圆C的标准方程;
(2)设直线l:y=kx+m与椭圆C交于A,B两点,点Q
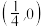 ,若|AQ|=|BQ|,求k的取值范围.
,若|AQ|=|BQ|,求k的取值范围.
您最近一年使用:0次
2020-12-11更新
|
644次组卷
|
6卷引用:江西省上高二中2022-2023学年高二上学期期中数学小练卷试题(1)
2020高三·全国·专题练习
名校
解题方法
10 . 已知椭圆 :
: (
( )的四个顶点组成的四边形的面积为
)的四个顶点组成的四边形的面积为 ,且经过点
,且经过点 .过椭圆右焦点
.过椭圆右焦点 作直线
作直线 与椭圆
与椭圆 交于
交于 、
、 两点.
两点.
(1)求椭圆 的方程;
的方程;
(2)若 ,求直线
,求直线 的方程.
的方程.
 :
: (
( )的四个顶点组成的四边形的面积为
)的四个顶点组成的四边形的面积为 ,且经过点
,且经过点 .过椭圆右焦点
.过椭圆右焦点 作直线
作直线 与椭圆
与椭圆 交于
交于 、
、 两点.
两点.(1)求椭圆
 的方程;
的方程;(2)若
 ,求直线
,求直线 的方程.
的方程.
您最近一年使用:0次
2020-12-06更新
|
2292次组卷
|
13卷引用:江西省南昌市第三中学2022-2023学年高二上学期期中考试数学试题
江西省南昌市第三中学2022-2023学年高二上学期期中考试数学试题黑龙江省双鸭山市饶河县高级中学2021-2022学年高二上学期期末数学试题(已下线)专题52 平面解析几何专题训练-2021年高考一轮数学(文)单元复习一遍过(已下线)专题55 平面解析几何专题训练-2021年高考一轮数学单元复习一遍过(新高考地区专用)(已下线)专题55 平面解析几何专题训练-2021年高考一轮数学(理)单元复习一遍过吉林省四平市公主岭市范家屯镇第一中学两校联考2021届高三上学期期末数学(理)试题吉林省四平市公主岭市范家屯镇第一中学两校联考2021届高三上学期期末数学(文)试题陕西省宝鸡市金台区2020-2021学年高二上学期期末数学(文)试题(已下线)专题12 选择性必修第一册综合练习-(新教材)2020-2021学年高二数学单元复习(人教A版选择性必修第一册)(已下线)第3章 圆锥曲线的方程-2021-2022学年高二数学课后培优练(人教A版2019选择性必修第一册)(已下线)选择性必修第一册 综合测试(基础)-2021-2022学年高二数学一隅三反系列(人教A版2019选择性必修第一册)广东省广州市增城区增城中学2021-2022学年高二上学期第二阶段测试数学试题(已下线)第29节 椭圆



