名校
解题方法
1 . 已知椭圆 过点
过点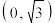 ,且离心率为
,且离心率为 .设
.设 ,
, 为椭圆
为椭圆 的左、右顶点,
的左、右顶点, 为椭圆上异于
为椭圆上异于 ,
, 的一点,直线
的一点,直线 ,
, 分别与直线
分别与直线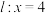 相交于
相交于 ,
, 两点,且直线
两点,且直线 与椭圆
与椭圆 交于另一点
交于另一点 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)求证:直线 与
与 的斜率之积为定值;
的斜率之积为定值;
(3)判断三点 ,
, ,
, 是否共线:并证明你的结论.
是否共线:并证明你的结论.
 过点
过点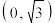 ,且离心率为
,且离心率为 .设
.设 ,
, 为椭圆
为椭圆 的左、右顶点,
的左、右顶点, 为椭圆上异于
为椭圆上异于 ,
, 的一点,直线
的一点,直线 ,
, 分别与直线
分别与直线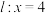 相交于
相交于 ,
, 两点,且直线
两点,且直线 与椭圆
与椭圆 交于另一点
交于另一点 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)求证:直线
 与
与 的斜率之积为定值;
的斜率之积为定值;(3)判断三点
 ,
, ,
, 是否共线:并证明你的结论.
是否共线:并证明你的结论.
您最近一年使用:0次
2022-10-11更新
|
1856次组卷
|
11卷引用:上海市2022届高三上学期一模暨春考模拟卷(五)数学试题
上海市2022届高三上学期一模暨春考模拟卷(五)数学试题北京市第八中学2023届高三上学期10月月考数学试题上海市青浦高级中学2022届高三下学期3月月考数学试题【区级联考】北京市昌平区2019届高三第一学期期末数学(文)试题(已下线)2020届北京四中高三第二学期开学考试数学试题江苏省金陵中学集团南京市人民中学2021-2022学年高二上学期10月月考数学试题北京市西城区回民学校2024届高三上学期12月月考数学试题天津市滨海新区塘沽紫云中学2024届高三上学期期末模拟数学试题(六)福建省莆田市第二中学2023-2024学年高二下学期返校考试数学试卷(已下线)第10题 椭圆中的一类定值问题 (压轴题)广东省深圳市翠园中学2024-2025学年高二上学期期中考试数学试题
名校
解题方法
2 . 已知椭圆C: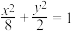 ,点E(-4,0),过点E作斜率大于0的直线与椭圆C相切,切点为T.
,点E(-4,0),过点E作斜率大于0的直线与椭圆C相切,切点为T.
(1)求点T的坐标;
(2)过线段ET的中点G作直线l交椭圆C于A,B两点,直线EA与椭圆C的另一个交点为M,直线EB与椭圆C的另一个交点为N,求证: ;
;
(3)请结合(2)的问题解决,运用类比推理,猜想写出抛物线中与之对应的一个相关结论(无需证明).
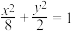 ,点E(-4,0),过点E作斜率大于0的直线与椭圆C相切,切点为T.
,点E(-4,0),过点E作斜率大于0的直线与椭圆C相切,切点为T.(1)求点T的坐标;
(2)过线段ET的中点G作直线l交椭圆C于A,B两点,直线EA与椭圆C的另一个交点为M,直线EB与椭圆C的另一个交点为N,求证:
 ;
;(3)请结合(2)的问题解决,运用类比推理,猜想写出抛物线中与之对应的一个相关结论(无需证明).
您最近一年使用:0次
2022-05-08更新
|
425次组卷
|
2卷引用:黑龙江省哈尔滨师范大学附属中学2022届高三第三次模拟考试理科数学试题
名校
解题方法
3 . 已知椭圆 :
:
 的离心率为
的离心率为 ,长轴的右端点为
,长轴的右端点为 .
.
(1)求 的方程;
的方程;
(2)直线 与椭圆
与椭圆 分别相交于
分别相交于 两点,且
两点,且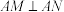 ,点
,点 不在直线
不在直线 上.
上.
①试证明直线 过一定点,并求出此定点;
过一定点,并求出此定点;
②从点 作
作 垂足为
垂足为 ,点
,点 ,写出
,写出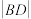 的最小值(结论不要求证明).
的最小值(结论不要求证明).
 :
:
 的离心率为
的离心率为 ,长轴的右端点为
,长轴的右端点为 .
.(1)求
 的方程;
的方程;(2)直线
 与椭圆
与椭圆 分别相交于
分别相交于 两点,且
两点,且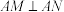 ,点
,点 不在直线
不在直线 上.
上.①试证明直线
 过一定点,并求出此定点;
过一定点,并求出此定点;②从点
 作
作 垂足为
垂足为 ,点
,点 ,写出
,写出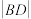 的最小值(结论不要求证明).
的最小值(结论不要求证明).
您最近一年使用:0次
2022-04-01更新
|
879次组卷
|
3卷引用:北京市门头沟区2022届高三一模数学试题
名校
解题方法
4 . 已知椭圆 :
: 的左、右焦点分别为
的左、右焦点分别为 ,
, ,
, 为椭圆上一动点(异于左、右顶点),若
为椭圆上一动点(异于左、右顶点),若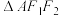 的周长为6,且面积的最大值为
的周长为6,且面积的最大值为 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)过点 作不与
作不与 轴重合的直线与椭圆
轴重合的直线与椭圆 相交于
相交于 ,
, 两点,直线
两点,直线 的方程为:
的方程为: ,过点
,过点 作
作 垂直于直线
垂直于直线 于点
于点 ,求证:直线
,求证:直线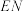 必过
必过 轴一定点.
轴一定点.
 :
: 的左、右焦点分别为
的左、右焦点分别为 ,
, ,
, 为椭圆上一动点(异于左、右顶点),若
为椭圆上一动点(异于左、右顶点),若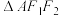 的周长为6,且面积的最大值为
的周长为6,且面积的最大值为 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)过点
 作不与
作不与 轴重合的直线与椭圆
轴重合的直线与椭圆 相交于
相交于 ,
, 两点,直线
两点,直线 的方程为:
的方程为: ,过点
,过点 作
作 垂直于直线
垂直于直线 于点
于点 ,求证:直线
,求证:直线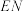 必过
必过 轴一定点.
轴一定点.
您最近一年使用:0次
2024-02-27更新
|
439次组卷
|
4卷引用:1号卷·2022年高考最新原创信息试卷(一)理数
解题方法
5 . 已知椭圆 :
: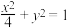 的左、右顶点分别为
的左、右顶点分别为 ,
, ,点
,点 (
(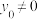 )在椭圆
)在椭圆 上,若点
上,若点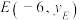 ,
,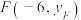 分别在直线
分别在直线 ,
,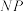 上.
上.
(1)求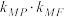 的值;
的值;
(2)连接 并延长交椭圆
并延长交椭圆 于点
于点 ,求证:
,求证: ,
, ,
, 三点共线.
三点共线.
 :
: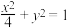 的左、右顶点分别为
的左、右顶点分别为 ,
, ,点
,点 (
(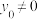 )在椭圆
)在椭圆 上,若点
上,若点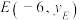 ,
,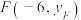 分别在直线
分别在直线 ,
,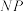 上.
上.(1)求
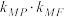 的值;
的值;(2)连接
 并延长交椭圆
并延长交椭圆 于点
于点 ,求证:
,求证: ,
, ,
, 三点共线.
三点共线.
您最近一年使用:0次
2024-03-11更新
|
637次组卷
|
3卷引用:1号卷·2022年高考最新原创信息试卷(二)理数
6 . 椭圆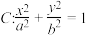 的右焦点为
的右焦点为 ,离心率为
,离心率为 .
.
(1)求椭圆C的方程;
(2)过F且斜率为1的直线交椭圆于M,N两点,P是直线x=4上任意一点.求证:直线PM,PF,PN的斜率成等差数列.
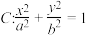 的右焦点为
的右焦点为 ,离心率为
,离心率为 .
.(1)求椭圆C的方程;
(2)过F且斜率为1的直线交椭圆于M,N两点,P是直线x=4上任意一点.求证:直线PM,PF,PN的斜率成等差数列.
您最近一年使用:0次
2022·全国·模拟预测
解题方法
7 . 已知椭圆 的左焦点为F,右顶点为
的左焦点为F,右顶点为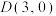 ,过F且斜率不为0的直线l交椭圆于A,B两点,C为线段AB的中点,当直线l的斜率为1时,线段AB的垂直平分线交x轴于点O(O为坐标原点),且
,过F且斜率不为0的直线l交椭圆于A,B两点,C为线段AB的中点,当直线l的斜率为1时,线段AB的垂直平分线交x轴于点O(O为坐标原点),且 .
.
(1)求椭圆的标准方程;
(2)若直线DA,DB分别交直线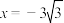 于点M,N,求证:以MN为直径的圆恒过点F.
于点M,N,求证:以MN为直径的圆恒过点F.
 的左焦点为F,右顶点为
的左焦点为F,右顶点为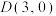 ,过F且斜率不为0的直线l交椭圆于A,B两点,C为线段AB的中点,当直线l的斜率为1时,线段AB的垂直平分线交x轴于点O(O为坐标原点),且
,过F且斜率不为0的直线l交椭圆于A,B两点,C为线段AB的中点,当直线l的斜率为1时,线段AB的垂直平分线交x轴于点O(O为坐标原点),且 .
.(1)求椭圆的标准方程;
(2)若直线DA,DB分别交直线
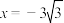 于点M,N,求证:以MN为直径的圆恒过点F.
于点M,N,求证:以MN为直径的圆恒过点F.
您最近一年使用:0次
解题方法
8 . 已知A′,A分别是椭圆C: (a>b>0)的左、右顶点,B,F分别是C的上顶点和左焦点.点P在C上,满足PF⊥A′A,AB∥OP,|FA′|=2
(a>b>0)的左、右顶点,B,F分别是C的上顶点和左焦点.点P在C上,满足PF⊥A′A,AB∥OP,|FA′|=2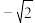 .
.
(1)求C的方程;
(2)过点F作直线l(与x轴不重合)交C于M,N两点,设直线AM,AN的斜率分别为k1,k2,求证:k1k2为定值.
 (a>b>0)的左、右顶点,B,F分别是C的上顶点和左焦点.点P在C上,满足PF⊥A′A,AB∥OP,|FA′|=2
(a>b>0)的左、右顶点,B,F分别是C的上顶点和左焦点.点P在C上,满足PF⊥A′A,AB∥OP,|FA′|=2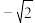 .
.(1)求C的方程;
(2)过点F作直线l(与x轴不重合)交C于M,N两点,设直线AM,AN的斜率分别为k1,k2,求证:k1k2为定值.
您最近一年使用:0次
解题方法
9 . 已知椭圆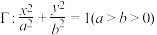 的右顶点坐标为A(2,0),左、右焦点分别为F1、F2,且|F1F2|=2,直线l交椭圆Γ于不同的两点M和N.
的右顶点坐标为A(2,0),左、右焦点分别为F1、F2,且|F1F2|=2,直线l交椭圆Γ于不同的两点M和N.
(1)求椭圆Γ的方程;
(2)若直线l的斜率为1,且以MN为直径的圆经过点A,求直线l的方程;
(3)若直线l与椭圆Γ相切,求证:点F1、F2到直线l的距离之积为定值.
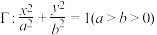 的右顶点坐标为A(2,0),左、右焦点分别为F1、F2,且|F1F2|=2,直线l交椭圆Γ于不同的两点M和N.
的右顶点坐标为A(2,0),左、右焦点分别为F1、F2,且|F1F2|=2,直线l交椭圆Γ于不同的两点M和N.(1)求椭圆Γ的方程;
(2)若直线l的斜率为1,且以MN为直径的圆经过点A,求直线l的方程;
(3)若直线l与椭圆Γ相切,求证:点F1、F2到直线l的距离之积为定值.
您最近一年使用:0次
名校
解题方法
10 . 已知点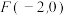 是椭圆
是椭圆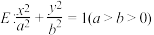 的左焦点,过
的左焦点,过 且垂直
且垂直 轴的直线
轴的直线 交
交 于
于 ,
, ,且
,且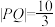 .
.
(1)求椭圆 的方程
的方程
(2)四边形 (A,D在
(A,D在 轴上方
轴上方 的四个顶点都在椭圆
的四个顶点都在椭圆 上,对角线
上,对角线 ,
, 恰好交于点
恰好交于点 ,若直线
,若直线 ,
, 分别与直线
分别与直线 交于
交于 ,
, ,且
,且 为坐标原点,求证:
为坐标原点,求证: .
.
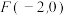 是椭圆
是椭圆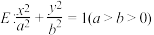 的左焦点,过
的左焦点,过 且垂直
且垂直 轴的直线
轴的直线 交
交 于
于 ,
, ,且
,且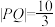 .
.(1)求椭圆
 的方程
的方程
(2)四边形
 (A,D在
(A,D在 轴上方
轴上方 的四个顶点都在椭圆
的四个顶点都在椭圆 上,对角线
上,对角线 ,
, 恰好交于点
恰好交于点 ,若直线
,若直线 ,
, 分别与直线
分别与直线 交于
交于 ,
, ,且
,且 为坐标原点,求证:
为坐标原点,求证: .
.
您最近一年使用:0次
2022-09-09更新
|
1131次组卷
|
4卷引用:湖南省益阳市2022-2023学年高三上学期9月质量检测数学试题
湖南省益阳市2022-2023学年高三上学期9月质量检测数学试题广东省广州市第五中学2023届高三上学期10月月考数学试题(已下线)专题39 圆锥曲线中的定点、定值问题-2(已下线)重难点突破16 圆锥曲线中的定点、定值问题 (十大题型)-2



