解题方法
1 . 有两位射击运动员在一次射击测试中各射靶10次,每次命中的环数如下:
甲:7 8 7 9 5 4 9 10 7 4
乙:9 5 7 8 7 6 8 6 7 7
(1)甲、乙两人本次射击的平均成绩分别为多少环?
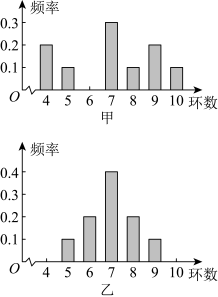
(2)观察下图中两人成绩的频率分布条形图,你能说明其水平差异在哪里吗?
甲:7 8 7 9 5 4 9 10 7 4
乙:9 5 7 8 7 6 8 6 7 7
(1)甲、乙两人本次射击的平均成绩分别为多少环?
(2)观察下图中两人成绩的频率分布条形图,你能说明其水平差异在哪里吗?
您最近一年使用:0次
名校
2 . 在某果园的苗圃进行果苗病虫害调查,随机调查了200棵受到某病虫害的果苗,并测量其高度 (单位:
(单位: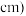 ,得到如下的样本数据的频率分布直方图.
,得到如下的样本数据的频率分布直方图.
(2)估计该苗圃一棵受到这种病虫害的果苗高度位于区间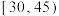 的概率;
的概率;
(3)已知该苗圃的果苗受到这种病虫害的概率为 ,果苗高度位于区间
,果苗高度位于区间 的棵数占该果苗总棵数的
的棵数占该果苗总棵数的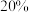 .从该苗圃中任选一棵高度位于区间
.从该苗圃中任选一棵高度位于区间 的果苗,求该棵果苗受到这种病虫害的概率(以样本数据中受到病虫害果苗的高度位于各区间的频率作为受到病虫害果苗的高度位于该区间的概率).
的果苗,求该棵果苗受到这种病虫害的概率(以样本数据中受到病虫害果苗的高度位于各区间的频率作为受到病虫害果苗的高度位于该区间的概率).
 (单位:
(单位: ,得到如下的样本数据的频率分布直方图.
,得到如下的样本数据的频率分布直方图.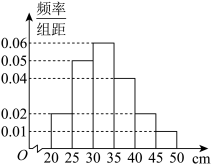
(2)估计该苗圃一棵受到这种病虫害的果苗高度位于区间
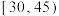 的概率;
的概率;(3)已知该苗圃的果苗受到这种病虫害的概率为
 ,果苗高度位于区间
,果苗高度位于区间 的棵数占该果苗总棵数的
的棵数占该果苗总棵数的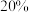 .从该苗圃中任选一棵高度位于区间
.从该苗圃中任选一棵高度位于区间 的果苗,求该棵果苗受到这种病虫害的概率(以样本数据中受到病虫害果苗的高度位于各区间的频率作为受到病虫害果苗的高度位于该区间的概率).
的果苗,求该棵果苗受到这种病虫害的概率(以样本数据中受到病虫害果苗的高度位于各区间的频率作为受到病虫害果苗的高度位于该区间的概率).
您最近一年使用:0次
2024-02-29更新
|
1078次组卷
|
9卷引用:8.1 条件概率(七大题型)-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)
(已下线)8.1 条件概率(七大题型)-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)(已下线)第7.1.1讲 条件概率-2023-2024学年新高二数学同步精讲精练宝典(人教A版2019选修第三册)四川省大数据精准教学联盟2024届高三第一次统一监测理科数学试题(已下线)7.1.1条件概率(分层练习,4大题型)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)(已下线)宁夏回族自治区石嘴山市平罗中学2024届高三下学期第一次模拟考试数学(理)试题(已下线)第8章 概率 章末题型归纳总结-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)黑龙江省牡丹江市第二高级中学2023-2024学年高二下学期4月月考数学试题(已下线)专题07 概率与统计综合问题(6类题型)-备战2023-2024学年高二数学下学期期末真题分类汇编(江苏专用)吉林省白城市洮北区白城市实验高级中学2023-2024学年高二下学期7月期末考试数学试题
名校
解题方法
3 . 某高中为了了解高中学生暑假期间阅读古典名著的时间 (小时/每周)和他们的语文成绩
(小时/每周)和他们的语文成绩 (分)的关系,某实验小组做了调查,得到一些数据(表一).
(分)的关系,某实验小组做了调查,得到一些数据(表一).
表一
(1)请根据所给数据求出语文成绩 的平均数和方差;
的平均数和方差;
(2)基于上述调查,学校为了确认学生喜欢阅读古典名著与语文成绩的关系,抽样调查了200位学生.按照是否喜欢阅读古典名著与语文成绩是否优秀统计,得到下列数据,请依据表中数据及小概率值 的独立性检验,分析“喜欢阅读古典名著与语文成绩优秀”是否有关.
的独立性检验,分析“喜欢阅读古典名著与语文成绩优秀”是否有关.
表二

 (小时/每周)和他们的语文成绩
(小时/每周)和他们的语文成绩 (分)的关系,某实验小组做了调查,得到一些数据(表一).
(分)的关系,某实验小组做了调查,得到一些数据(表一).表一
| 编号 | 1 | 2 | 3 | 4 | 5 |
学习时间 | 2 | 4 | 7 | 7 | 10 |
语文成绩 | 82 | 93 | 95 | 108 | 122 |
 的平均数和方差;
的平均数和方差;(2)基于上述调查,学校为了确认学生喜欢阅读古典名著与语文成绩的关系,抽样调查了200位学生.按照是否喜欢阅读古典名著与语文成绩是否优秀统计,得到下列数据,请依据表中数据及小概率值
 的独立性检验,分析“喜欢阅读古典名著与语文成绩优秀”是否有关.
的独立性检验,分析“喜欢阅读古典名著与语文成绩优秀”是否有关.表二
| 语文成绩优秀 | 语文成绩不优秀 | 合计 | |
| 喜欢阅读 | 75 | 25 | 100 |
| 不喜欢阅读 | 55 | 45 | 100 |
| 合计 | 130 | 70 | 200 |

 | 0.10 | 0.05 | 0.010 |
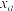 | 2.706 | 3.841 | 6.635 |
您最近一年使用:0次
名校
解题方法
4 . 从某企业生产的某种产品中随机抽取1000件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图: 和样本方差
和样本方差 (同一组的数据用该组区间的中点值作为代表);
(同一组的数据用该组区间的中点值作为代表);
(2)由直方图可以认为,这种产品的质量指标值 服从正态分布
服从正态分布 ,其中
,其中 近似为样本平均数
近似为样本平均数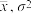 近似为样本方差
近似为样本方差 ,为监控该产品的生产质量,每天抽取10个产品进行检测,若出现了质量指标值在
,为监控该产品的生产质量,每天抽取10个产品进行检测,若出现了质量指标值在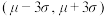 之外的产品,就认为这一天的生产过程中可能出现了异常情况,需对当天的生产过程进行检查.
之外的产品,就认为这一天的生产过程中可能出现了异常情况,需对当天的生产过程进行检查.
①假设生产状态正常,记 表示一天内抽取的10个产品中尺寸在
表示一天内抽取的10个产品中尺寸在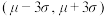 之外的产品数,求
之外的产品数,求
②请说明上述监控生产过程方法的合理性.
附: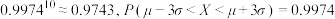
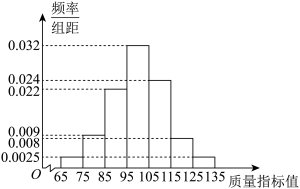
 和样本方差
和样本方差 (同一组的数据用该组区间的中点值作为代表);
(同一组的数据用该组区间的中点值作为代表);(2)由直方图可以认为,这种产品的质量指标值
 服从正态分布
服从正态分布 ,其中
,其中 近似为样本平均数
近似为样本平均数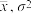 近似为样本方差
近似为样本方差 ,为监控该产品的生产质量,每天抽取10个产品进行检测,若出现了质量指标值在
,为监控该产品的生产质量,每天抽取10个产品进行检测,若出现了质量指标值在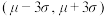 之外的产品,就认为这一天的生产过程中可能出现了异常情况,需对当天的生产过程进行检查.
之外的产品,就认为这一天的生产过程中可能出现了异常情况,需对当天的生产过程进行检查.①假设生产状态正常,记
 表示一天内抽取的10个产品中尺寸在
表示一天内抽取的10个产品中尺寸在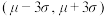 之外的产品数,求
之外的产品数,求
②请说明上述监控生产过程方法的合理性.
附:
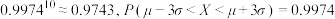
您最近一年使用:0次
2024-02-20更新
|
1047次组卷
|
4卷引用:8.3 正态分布(七大题型)-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)
(已下线)8.3 正态分布(七大题型)-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)重庆市第八中学校2023-2024学年高三下学期入学适应性考试数学试题(已下线)7.5 正态分布(分层练习,8大题型)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)(已下线)专题03 随机变量的分布列--高二期末考点大串讲(人教B版2019选择性必修第二册)
5 . 大学生刘铭去某工厂实习,实习结束时从自己制作的某种零件中随机选取了10个样品,测量每个零件的横截面积(单位: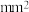 )和耗材量(单位:
)和耗材量(单位: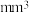 ),得到如下数据:
),得到如下数据:
并计算得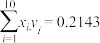 ,
,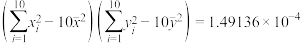 .
.
(1)估算刘铭同学制作的这种零件平均每个零件的横截面积以及平均一个零件的耗材量;
(2)求刘铭同学制作的这种零件的横截面积和耗材量的样本相关系数(精确到0.01).
附:相关系数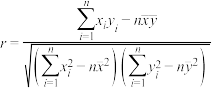 ;
;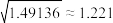 .
.
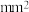 )和耗材量(单位:
)和耗材量(单位: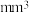 ),得到如下数据:
),得到如下数据:样本号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 总和 |
零件的横截面积 | 0.03 | 0.05 | 0.04 | 0.07 | 0.07 | 0.04 | 0.05 | 0.06 | 0.06 | 0.05 | 0.52 |
耗材量 | 0.24 | 0.40 | 0.23 | 0.55 | 0.50 | 0.34 | 0.35 | 0.45 | 0.43 | 0.41 | 3.9 |
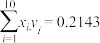 ,
,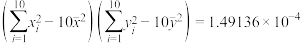 .
.(1)估算刘铭同学制作的这种零件平均每个零件的横截面积以及平均一个零件的耗材量;
(2)求刘铭同学制作的这种零件的横截面积和耗材量的样本相关系数(精确到0.01).
附:相关系数
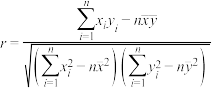 ;
;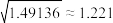 .
.
您最近一年使用:0次
2024-01-26更新
|
522次组卷
|
7卷引用:第05讲 第八章 成对数据的统计分析 章末重点题型大总结-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第三册)
(已下线)第05讲 第八章 成对数据的统计分析 章末重点题型大总结-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第三册)陕西省汉中市汉台区2024届高三上学期第四次校际联考数学(文)试题陕西省西安市西咸新区2024届高三上学期模拟考试数学(文)试题(已下线)8.1 成对数据的统计相关性(分层练习,5大题型)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)(已下线)8.1.1变量的相关关系+8.1.2样本相关系数 第三练 能力提升拔高单元测试B卷——第八章 成对数据的统计分析(已下线)专题4.1 数据的相关性及回归方程(八个重难点突破)-2023-2024学年高二数学下学期重难点突破及混淆易错规避(人教A版2019)
解题方法
6 . 坐位体前屈是中小学体质健康测试项目,主要测试学生躯干、腰、髋等部位关节韧带和肌肉的伸展性、弹性及身体柔韧性,在对某高中1500名高三年级学生的坐位体前屈成绩的调查中,采用按学生性别比例分配的分层随机抽样抽取100人,已知这1500名高三年级学生中男生有900人,且抽取的样本中男生的平均数和方差分别为13.2cm和13.36,女生的平均数和方差分别为15.2cm和17.56.
(1)求抽取的总样本的平均数;
(2)试估计高三年级全体学生的坐位体前屈成绩的方差.
参考公式:总体分为2层,分层随机抽样,各层抽取的样本量、样本平均数和样本方差分别为: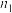 ,
, ,
, ,
,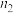 ,
,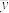 ,
, .记总样本的平均数为
.记总样本的平均数为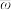 ,样本方差为
,样本方差为 ,
,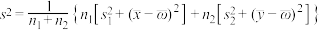
(1)求抽取的总样本的平均数;
(2)试估计高三年级全体学生的坐位体前屈成绩的方差.
参考公式:总体分为2层,分层随机抽样,各层抽取的样本量、样本平均数和样本方差分别为:
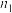 ,
, ,
, ,
,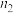 ,
,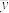 ,
, .记总样本的平均数为
.记总样本的平均数为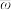 ,样本方差为
,样本方差为 ,
,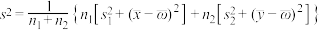
您最近一年使用:0次
2023-02-19更新
|
1202次组卷
|
9卷引用:【导学案】 6.4.2 用样本估计总体的离散程度 课前预习-湘教版(2019)必修(第一册) 第6章 统计学初步
【导学案】 6.4.2 用样本估计总体的离散程度 课前预习-湘教版(2019)必修(第一册) 第6章 统计学初步吉林省吉林市普通中学2022-2023学年高三第二次调研测试数学试题(已下线)专题10 计数原理与概率统计(文科)(已下线)专题15 押全国卷第19题 统计与概率(已下线)第九章 统计(基础检测卷)第九章 统计(A卷·基础提升练)-【单元测试】2022-2023学年高一数学分层训练AB卷(人教A版2019必修第二册)(已下线)9.2 用样本估计总体(精练)(1)(已下线)9.2 用样本估计总体(精练)-2022-2023学年高一数学一隅三反系列(人教A版2019必修第二册)陕西省西安工业大学附属中学2022-2023学年高一下学期第二次月考数学试题
名校
7 . 在一次高三年级统一考试中,数学试卷有一道满分为10分的选做题,学生可以从 ,
, 两道题目中任选一题作答.某校有900名高三学生参加了本次考试,为了了解该校学生解答该选做题的得分情况,计划从900名学生的选做题成绩中随机抽取一个容量为10的样本,为此将900名学生的选做题的成绩随机编号为001,002,
两道题目中任选一题作答.某校有900名高三学生参加了本次考试,为了了解该校学生解答该选做题的得分情况,计划从900名学生的选做题成绩中随机抽取一个容量为10的样本,为此将900名学生的选做题的成绩随机编号为001,002, ,900.
,900.
(1)若采用随机数法抽样,并按照以下随机数表,以方框内的数字5为起点,从左向右依次读数,每次读取三位随机数,一行数读完之后接下一行左端写出样本编号的中位数.
05 26 93 70 60 22 35 85 15 13 92 03 51 59 77
59 56 78 06 83 52 91 05 70 74 07 97 10 88 23
09 98 42 99 64 61 71 62 99 15 06 1 29 16 93
1 29 16 93
58 05 77 09 51 51 26 87 85 85 54 87 66 47 54
73 32 08 11 12 44 95 92 63 16 29 56 24 29 48
26 99 61 65 53 58 37 78 80 70 42 10 50 67 42
32 17 55 85 74 94 44 67 16 94 14 65 52 68 75
87 59 36 22 41 26 78 63 06 55 13 08 27 01 50
15 29 39 39 43
(2)若采用分层随机抽样,按照学生选择 题目或
题目或 题目,将成绩分为两层,且样本中选择
题目,将成绩分为两层,且样本中选择 题目的成绩有8个,平均数为7,方差为4;样本中选择
题目的成绩有8个,平均数为7,方差为4;样本中选择 题目的成绩有2个,平均数为8,方差为1.试用样本估计该校900名学生的选做题得分的平均数与方差.
题目的成绩有2个,平均数为8,方差为1.试用样本估计该校900名学生的选做题得分的平均数与方差.
 ,
, 两道题目中任选一题作答.某校有900名高三学生参加了本次考试,为了了解该校学生解答该选做题的得分情况,计划从900名学生的选做题成绩中随机抽取一个容量为10的样本,为此将900名学生的选做题的成绩随机编号为001,002,
两道题目中任选一题作答.某校有900名高三学生参加了本次考试,为了了解该校学生解答该选做题的得分情况,计划从900名学生的选做题成绩中随机抽取一个容量为10的样本,为此将900名学生的选做题的成绩随机编号为001,002, ,900.
,900.(1)若采用随机数法抽样,并按照以下随机数表,以方框内的数字5为起点,从左向右依次读数,每次读取三位随机数,一行数读完之后接下一行左端写出样本编号的中位数.
05 26 93 70 60 22 35 85 15 13 92 03 51 59 77
59 56 78 06 83 52 91 05 70 74 07 97 10 88 23
09 98 42 99 64 61 71 62 99 15 06
 1 29 16 93
1 29 16 9358 05 77 09 51 51 26 87 85 85 54 87 66 47 54
73 32 08 11 12 44 95 92 63 16 29 56 24 29 48
26 99 61 65 53 58 37 78 80 70 42 10 50 67 42
32 17 55 85 74 94 44 67 16 94 14 65 52 68 75
87 59 36 22 41 26 78 63 06 55 13 08 27 01 50
15 29 39 39 43
(2)若采用分层随机抽样,按照学生选择
 题目或
题目或 题目,将成绩分为两层,且样本中选择
题目,将成绩分为两层,且样本中选择 题目的成绩有8个,平均数为7,方差为4;样本中选择
题目的成绩有8个,平均数为7,方差为4;样本中选择 题目的成绩有2个,平均数为8,方差为1.试用样本估计该校900名学生的选做题得分的平均数与方差.
题目的成绩有2个,平均数为8,方差为1.试用样本估计该校900名学生的选做题得分的平均数与方差.
您最近一年使用:0次
2022-03-21更新
|
853次组卷
|
10卷引用:第7课时 课前 总体离散趋势的估计
第7课时 课前 总体离散趋势的估计北师大版(2019) 必修第一册 突围者 第六章 全章综合检测河南省南阳市第一中学校2021-2022学年高一上学期第四次月考数学试题(已下线)9.2 用样本估计总体~9.3 统计案例 公司员工的肥胖情况调查分析-2021-2022学年高一数学10分钟课前预习练(人教A版2019必修第二册)(已下线)第九章 统计(选拔卷)-【单元测试】2021-2022学年高一数学尖子生选拔卷(人教A版2019必修第二册)(已下线)专题11 灵活运用两种抽样-2021-2022学年高一数学下学期期末必考题型归纳及过关测试(人教A版2019)(已下线)专题12 频率分布直方图、样本估计总体-2021-2022学年高一数学下学期期末必考题型归纳及过关测试(人教A版2019)(已下线)第9.2讲 用样本估计总体(已下线)9.3 统计案例 公司员工的肥胖情况调查分析(分层作业)-【上好课】(已下线)13.5 统计估计
名校
解题方法
8 . 2020年某地在全国志愿服务信息系统注册登记志愿者8万多人.2019年7月份以来,共完成1931个志愿服务项目,8900多名志愿者开展志愿服务活动累计超过150万小时.为了了解此地志愿者对志愿服务的认知和参与度,随机调查了500名志愿者每月的志愿服务时长(单位:小时),并绘制如图所示的频率分布直方图.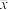 和样本方差
和样本方差 (同一组中的数据用该组区间的中间值代表);
(同一组中的数据用该组区间的中间值代表);
(2)由直方图可以认为,目前该地志愿者每月服务时长 服从正态分布
服从正态分布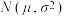 ,其中
,其中 近似为样本平均数
近似为样本平均数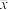 ,
, 近似为样本方差
近似为样本方差 .一般正态分布的概率都可以转化为标准正态分布的概率进行计算:若
.一般正态分布的概率都可以转化为标准正态分布的概率进行计算:若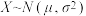 ,令
,令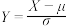 ,则
,则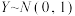 ,且
,且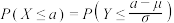 .
.
(ⅰ)利用直方图得到的正态分布,求 ;
;
(ⅱ)从该地随机抽取20名志愿者,记 表示这20名志愿者中每月志愿服务时长超过10小时的人数,求
表示这20名志愿者中每月志愿服务时长超过10小时的人数,求 (结果精确到0.001)以及
(结果精确到0.001)以及 的数学期望.
的数学期望.
参考数据: ,
,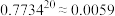 .若
.若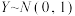 ,则
,则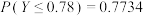 .
.

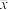 和样本方差
和样本方差 (同一组中的数据用该组区间的中间值代表);
(同一组中的数据用该组区间的中间值代表);(2)由直方图可以认为,目前该地志愿者每月服务时长
 服从正态分布
服从正态分布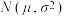 ,其中
,其中 近似为样本平均数
近似为样本平均数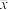 ,
, 近似为样本方差
近似为样本方差 .一般正态分布的概率都可以转化为标准正态分布的概率进行计算:若
.一般正态分布的概率都可以转化为标准正态分布的概率进行计算:若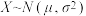 ,令
,令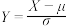 ,则
,则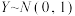 ,且
,且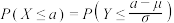 .
.(ⅰ)利用直方图得到的正态分布,求
 ;
;(ⅱ)从该地随机抽取20名志愿者,记
 表示这20名志愿者中每月志愿服务时长超过10小时的人数,求
表示这20名志愿者中每月志愿服务时长超过10小时的人数,求 (结果精确到0.001)以及
(结果精确到0.001)以及 的数学期望.
的数学期望.参考数据:
 ,
,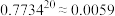 .若
.若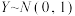 ,则
,则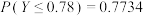 .
.
您最近一年使用:0次
2021-03-23更新
|
3337次组卷
|
16卷引用:8.3 正态分布(七大题型)-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)
(已下线)8.3 正态分布(七大题型)-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)河南省济源(平顶山许昌市)2021届高三第二次质量检测理科数学试题(已下线)黄金卷20-【赢在高考·黄金20卷】备战2021年高考数学全真模拟卷(山东高考专用)(已下线)专题23 概率与统计相结合问题(讲)-2021年高三数学二轮复习讲练测(新高考版)(已下线)专题27 概率与统计相结合问题(讲)-2021年高三数学二轮复习讲练测(文理通用)(已下线)专题7.6第七章《随机变量及其分布列》综合测试卷(B卷提升篇)-2020-2021学年高二下学期数学选择性必修第三册同步单元AB卷(新教材人教A版,浙江专用)辽宁省部分重点高中2020-2021学年高二下学期期中考试数学试题安徽省六安市舒城中学2021届高三下学期仿真模拟(三)理科数学试题(已下线)解密21 统计与概率(分层训练)-【高频考点解密】2021年高考数学(理)二轮复习讲义+分层训练(已下线)押第18题 概率与统计-备战2021年高考数学(理)临考题号押题(全国卷2)(已下线)7.5正态分布B卷(已下线)专题50 正态分布-2山西省2024届高三上学期优生联考数学试题黑龙江省齐齐哈尔市龙西北高中名校联盟2023-2024学年高三上学期期末联合考试数学试题(已下线)第08讲 7.5 正态分布(1)(已下线)第08讲 两点分布、二项分布、超几何分布与正态分布(十一大题型)(练习)-1
9 . 某中学举行电脑知识竞赛,现将高一参赛学生的成绩进行整理后分成五组绘制成如图所示的频率分布直方图;
(2)求高一参赛学生的平均成绩.

(2)求高一参赛学生的平均成绩.
您最近一年使用:0次
2020-07-24更新
|
1986次组卷
|
6卷引用:【导学案】 6.4.3 用频率分布直方图估计总体分布 课前预习-湘教版(2019)必修(第一册) 第6章 统计学初步
10 . 从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量表得如下频数分布表:
(I)在答题卡上作出这些数据的频率分布直方图:
(III)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定?
| 质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
| 频数 | 6 | 26 | 38 | 22 | 8 |
(I)在答题卡上作出这些数据的频率分布直方图:
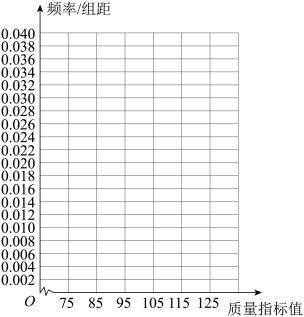
(III)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定?
您最近一年使用:0次
2019-01-30更新
|
14789次组卷
|
50卷引用:【导学案】 6.4.3 用频率分布直方图估计总体分布 课前预习-湘教版(2019)必修(第一册) 第6章 统计学初步
【导学案】 6.4.3 用频率分布直方图估计总体分布 课前预习-湘教版(2019)必修(第一册) 第6章 统计学初步2014年全国普通高等学校招生统一考试文科数学(新课标Ⅰ)2015-2016学年湖北省襄州一中等四校高二上学期期中理科数学试卷2015-2016学年山西省临汾市一中高一12月月考数学试卷2016年内蒙古包头市高三学业水平测试与评估(二)数学文试卷广西宾阳县宾阳中学2017-2018学年高二9月月考数学试题人教B版高中数学必修三同步测试:模块复习课2统计【全国校级联考】河北省石家庄市行唐县三中、正定县三中、正定县七中2017届高三12月联考数学(文)试卷【全国百强校】广东省深圳市高级中学2019届高三12月模拟考试数学(文)试题【全国百强校】四川外语学院重庆第二外国语学校2017届高三下学期第二次检测数学(文)试题【市级联考】湖南省衡阳市2019届高三下学期第一次联考数学(文)试题【全国百强校】湖南省衡阳市第一中学2018-2019学年高二下学期第一次月考数学(文)试题人教A版高中数学必修三 第二章2.2-2.2.2用样本的数字特征估计总体的数字特征2人教B版(2019) 必修第二册 过关斩将 第五章 5.1 综合拔高练四川省成都市成都市第七中学2019-2020学年高二上学期期中数学(文)试题(已下线)专题10.2 用样本估计总体(练)【理】-《2020年高考一轮复习讲练测》专题10.2 统计与统计案例(讲) -江苏版《2020年高考一轮复习讲练测》人教A版(2019) 必修第二册 突围者(经验篇) 第9章 第1节随机抽样+第2节用样本估计总体.内蒙古北方重工业集团有限公司第三中学2017-2018学年高二上学期期中数学(文)试题2020届全国100所名校高考模拟金典卷高三文科数学(八)试题2019届湖南省衡阳市高三第一次模拟文科数学试题(已下线)专题16 用样本估计总体、统计案例(核心素养练习)-【新教材精创】2019-2020高一数学新教材知识讲学(人教A版必修第二册)-《高中新教材知识讲学》吉林省松原市实验中学2020届高考数学(文科)八模试卷(已下线)第六章测评-【新教材】北师大版(2019)高中数学必修第一册练习(已下线)综合测试卷(基础版)突破满分数学之2019-2020学年高二数学(理)重难点突破(人教A版选修2-3)(已下线)专题31 概率和统计【文】-十年(2011-2020)高考真题数学分项(已下线)专题32 概率和统计【理】-十年(2011-2020)高考真题数学分项(六)江苏省南通市启东中学2020-2021学年高二上学期期初考试数学试题广东省广大附中、铁一、广外三校2020-2021学年高一下学期期中联考数学试题江西省靖安中学2021届高三上学期第四次月考数学(文)试题(已下线)专题14 概率统计-十年(2012-2021)高考数学真题分项汇编(全国通用)重庆市江津中学2020-2021学年高一下学期第三阶段考试数学试题湘教版(2019) 必修第一册 突围者 第6章 第四节 课时3 用频率分布直方图估计总体分布宁夏青铜峡市高级中学2021-2022学年高二11月测试数学(理)试题(已下线)考向50 抽样方法与总体分布的估计(已下线)习题6.4第五章 统计与概率章末检测(能力篇)-2021-2022学年高一数学同步知识梳理+考点精讲精练(人教B版2019必修第二册)沪教版(2020) 必修第三册 精准辅导 第13章 单元测试(已下线)专题14 概率统计解答题-22023版 湘教版(2019) 必修第一册 突围者 第6章 第四节 课时3 用频率分布直方图估计总体分布第13章 统计(单元提升卷)-2022-2023学年高二数学考试满分全攻略(沪教版2020必修第三册)第六章 统计综合拔高练习-2021-2022学年高一上学期数学北师大版(2019)必修第一册第九章 统计(B卷·能力提升练)-【单元测试】2022-2023学年高一数学分层训练AB卷(人教A版2019必修第二册)北师大版(2019) 必修第一册 章末检测卷(六)统计湘教版(2019)必修第一册课本习题 习题6.4(已下线)第十四章 统计(压轴题专练)--单元速记·巧练(苏教版2019必修第二册)(已下线)9.1 随机抽样与统计图标(高考真题素材之十年高考)(已下线)专题25 概率统计解答题(文科)(已下线)9.2.2总体百分位数的估计+9.2.3总体集中趋势的估计+9.2.4总体离散程度的估计【第三练】“上好三节课,做好三套题“高中数学素养晋级之路(已下线)第四章 统计 专题一 用样本估计总体 微点2 用样本估计总体(二)【培优版】






