1 . 若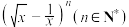 的二项展开式的第9项为常数项,则
的二项展开式的第9项为常数项,则
________
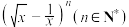 的二项展开式的第9项为常数项,则
的二项展开式的第9项为常数项,则
您最近一年使用:0次
2024-01-14更新
|
387次组卷
|
4卷引用:上海市嘉定区上海师范大学附属嘉定高级中学2023学年高二下学期期中考试数学试卷
上海市嘉定区上海师范大学附属嘉定高级中学2023学年高二下学期期中考试数学试卷上海市松江二中2023-2024学年高二上学期期末考试数学试题(已下线)第六章 计数原理(知识归纳+题型突破)(4)(已下线)专题02 计数原理-2
解题方法
2 . 若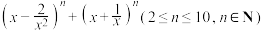 的展开式中存在常数项,则下列选项中
的展开式中存在常数项,则下列选项中 的取值不可能是( )
的取值不可能是( )
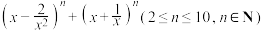 的展开式中存在常数项,则下列选项中
的展开式中存在常数项,则下列选项中 的取值不可能是( )
的取值不可能是( )A. | B. | C. | D. |
您最近一年使用:0次
2023-12-21更新
|
1124次组卷
|
6卷引用:上海市奉贤区2024届高三一模数学试题
上海市奉贤区2024届高三一模数学试题(已下线)第六章 计数原理(知识归纳+题型突破)(4)上海市莘庄中学2023-2024学年高二下学期期中考试数学试卷(已下线)专题19 排列组合与二项式定理常考小题(20大核心考点)(讲义)(已下线)上海市奉贤区2024届高三一模数学试题变式题11-15(已下线)【练】专题八 与n个二项式和有关的问题(压轴大全)
名校
3 . 已知 为正整数,对于给定的函数
为正整数,对于给定的函数 ,定义一个
,定义一个 次多项式
次多项式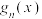 如下:
如下: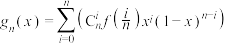
(1)当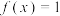 时,求
时,求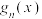 ;
;
(2)当 时,求
时,求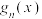 ;
;
(3)当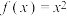 时,求
时,求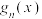 .
.
 为正整数,对于给定的函数
为正整数,对于给定的函数 ,定义一个
,定义一个 次多项式
次多项式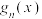 如下:
如下: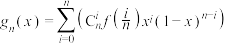
(1)当
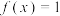 时,求
时,求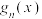 ;
;(2)当
 时,求
时,求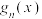 ;
;(3)当
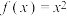 时,求
时,求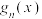 .
.
您最近一年使用:0次
名校
4 . 已知 ,设函数
,设函数 的表达式为
的表达式为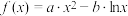 (其中
(其中 )
)
(1)设 ,
, ,当
,当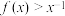 时,求x的取值范围;
时,求x的取值范围;
(2)设 ,
, ,集合
,集合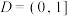 ,记
,记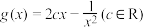 ,若
,若 在D上为严格增函数且对D上的任意两个变量s,t,均有
在D上为严格增函数且对D上的任意两个变量s,t,均有 成立,求c的取值范围;
成立,求c的取值范围;
(3)当 ,
, ,
, 时,记
时,记 ,其中n为正整数.求证:
,其中n为正整数.求证: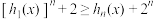 .
.
 ,设函数
,设函数 的表达式为
的表达式为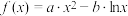 (其中
(其中 )
)(1)设
 ,
, ,当
,当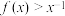 时,求x的取值范围;
时,求x的取值范围;(2)设
 ,
, ,集合
,集合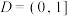 ,记
,记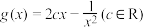 ,若
,若 在D上为严格增函数且对D上的任意两个变量s,t,均有
在D上为严格增函数且对D上的任意两个变量s,t,均有 成立,求c的取值范围;
成立,求c的取值范围;(3)当
 ,
, ,
, 时,记
时,记 ,其中n为正整数.求证:
,其中n为正整数.求证: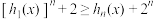 .
.
您最近一年使用:0次
2023-04-13更新
|
1690次组卷
|
5卷引用:上海市普陀区2023届高三二模数学试题
上海市普陀区2023届高三二模数学试题(已下线)重难点04导数的应用六种解法(1)天津市耀华中学2023届高三二模数学试题天津市南开中学2022-2023学年高二下学期期末数学试题(已下线)专题04 函数导数综合应用(四大题型)-【好题汇编】备战2023-2024学年高二数学下学期期末真题分类汇编(天津专用)
名校
解题方法
5 . “ ”是“
”是“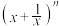 的二项展开式中存在常数项”的( )
的二项展开式中存在常数项”的( )
 ”是“
”是“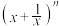 的二项展开式中存在常数项”的( )
的二项展开式中存在常数项”的( )| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
您最近一年使用:0次
2023-02-15更新
|
858次组卷
|
5卷引用:上海市闵行区2023届高三一模数学试题
上海市闵行区2023届高三一模数学试题(已下线)6.5二项式定理(分层练习)-2022-2023学年高二数学同步精品课堂(沪教版2020选择性必修第二册)上海市宜川中学2022-2023学年高二下学期期末数学试题上海市七宝中学2022届高三下学期高考模拟数学试题(已下线)专题一 集合与常用逻辑用语-2
23-24高二上·上海·期末
名校
解题方法
6 . 等差数列 的通项是
的通项是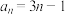 ,等比数列
,等比数列 满足
满足 ,
, ,其中
,其中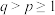 ,且
,且 、
、 、
、 均为正整数.有关数列
均为正整数.有关数列 ,有如下四个命题:
,有如下四个命题:
①存在 、
、 ,使得数列
,使得数列 的所有项均在数列
的所有项均在数列 中;
中;
②存在 、
、 ,使得数列
,使得数列 仅有有限项(至少1项)不在数列
仅有有限项(至少1项)不在数列 中;
中;
③存在 、
、 ,使得数列
,使得数列 的某一项的值为2023;
的某一项的值为2023;
④存在 、
、 ,使得数列
,使得数列 的前若干项的和为2023.
的前若干项的和为2023.
其中正确的命题个数是( )个
 的通项是
的通项是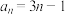 ,等比数列
,等比数列 满足
满足 ,
, ,其中
,其中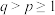 ,且
,且 、
、 、
、 均为正整数.有关数列
均为正整数.有关数列 ,有如下四个命题:
,有如下四个命题:①存在
 、
、 ,使得数列
,使得数列 的所有项均在数列
的所有项均在数列 中;
中;②存在
 、
、 ,使得数列
,使得数列 仅有有限项(至少1项)不在数列
仅有有限项(至少1项)不在数列 中;
中;③存在
 、
、 ,使得数列
,使得数列 的某一项的值为2023;
的某一项的值为2023;④存在
 、
、 ,使得数列
,使得数列 的前若干项的和为2023.
的前若干项的和为2023.其中正确的命题个数是( )个
| A.0 | B.1 | C.2 | D.3 |
您最近一年使用:0次
2023-01-20更新
|
933次组卷
|
6卷引用:上海期末数学练习
(已下线)上海期末数学练习(已下线)期末真题必刷压轴60题(22个考点专练)-【满分全攻略】2023-2024学年高二数学同步讲义全优学案(沪教版2020必修第三册)(已下线)专题17 数列探索型、存在型问题的解法 微点1 数列探索型问题的解法北京市第二十四中学2023-2024学年高二上学期期末数学模拟试卷(已下线)上海市高二下学期期末真题必刷04(压轴题)--高二期末考点大串讲(沪教版2020选修)(已下线)第一章 排列组合与二项式定理 专题五 二项式定理 微点3 二项式定理(三)【培优版】
名校
7 . 已知集合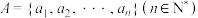 ,规定:若集合
,规定:若集合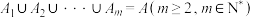 ,则称
,则称 为集合
为集合 的一个分拆,当且仅当:
的一个分拆,当且仅当: ,
, ,…,
,…, 时,
时, 与
与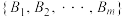 为同一分拆,所有不同的分拆种数记为
为同一分拆,所有不同的分拆种数记为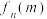 .例如:当
.例如:当 ,
, 时,集合
时,集合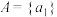 的所有分拆为:
的所有分拆为: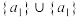 ,
,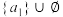 ,
,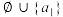 ,即
,即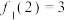 .
.
(1)求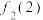 ;
;
(2)试用 、
、 表示
表示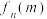 ;
;
(3)设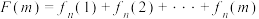 ,规定
,规定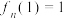 ,证明:当
,证明:当 时,
时,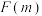 与
与 同为奇数或者同为偶数.
同为奇数或者同为偶数.
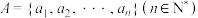 ,规定:若集合
,规定:若集合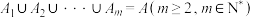 ,则称
,则称 为集合
为集合 的一个分拆,当且仅当:
的一个分拆,当且仅当: ,
, ,…,
,…, 时,
时, 与
与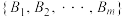 为同一分拆,所有不同的分拆种数记为
为同一分拆,所有不同的分拆种数记为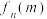 .例如:当
.例如:当 ,
, 时,集合
时,集合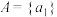 的所有分拆为:
的所有分拆为: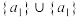 ,
,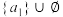 ,
,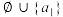 ,即
,即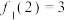 .
.(1)求
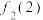 ;
;(2)试用
 、
、 表示
表示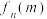 ;
;(3)设
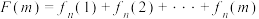 ,规定
,规定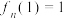 ,证明:当
,证明:当 时,
时,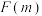 与
与 同为奇数或者同为偶数.
同为奇数或者同为偶数.
您最近一年使用:0次
2023-02-07更新
|
1292次组卷
|
11卷引用:6.5二项式定理(分层练习)-2022-2023学年高二数学同步精品课堂(沪教版2020选择性必修第二册)
(已下线)6.5二项式定理(分层练习)-2022-2023学年高二数学同步精品课堂(沪教版2020选择性必修第二册)(已下线)第6章 计数原理(B卷·能力提升练)-【单元测试】2022-2023学年高二数学分层训练AB卷(沪教版2020选择性必修第二册)(已下线)第6章 计数原理(基础、常考、易错、压轴)分类专项训练上海市实验学校2022-2023学年高二上学期期末数学试题(已下线)第六章 计数原理(压轴题专练)-2023-2024学年高二数学单元速记·巧练(沪教版2020选择性必修第二册)(已下线)专题15 二项式定理- 【暑假自学课】(沪教版2020)江西省吉安市峡江中学2023-2024学年高二上学期期末数学试卷(九省联考题型)(已下线)期中考试押题卷(考试范围:第6-7章)-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)单元测试B卷——第六章 计数原理(已下线)专题7 以新定义为背景的相关问题【练】(高二期末压轴专项)重庆市九龙坡区部分学校2023-2024学年高二下学期期中测试数学试题
名校
8 . 若 的展开式中共有7项,则常数项为
的展开式中共有7项,则常数项为___________ (用数字作答).
 的展开式中共有7项,则常数项为
的展开式中共有7项,则常数项为
您最近一年使用:0次
2021-09-05更新
|
554次组卷
|
4卷引用:上海市格致中学2023届高三三模数学试题
9 . 已知数列 的首项为1.记
的首项为1.记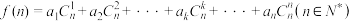 .
.
(1)若 为常数列,求
为常数列,求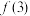 的值:
的值:
(2)若 为公比为2的等比数列,求
为公比为2的等比数列,求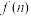 的解析式:
的解析式:
(3)是否存在等差数列 ,使得
,使得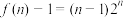 对一切
对一切 都成立?若存在,求出数列
都成立?若存在,求出数列 的通项公式:若不存在,请说明理由.
的通项公式:若不存在,请说明理由.
 的首项为1.记
的首项为1.记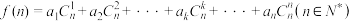 .
.(1)若
 为常数列,求
为常数列,求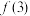 的值:
的值:(2)若
 为公比为2的等比数列,求
为公比为2的等比数列,求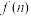 的解析式:
的解析式:(3)是否存在等差数列
 ,使得
,使得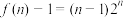 对一切
对一切 都成立?若存在,求出数列
都成立?若存在,求出数列 的通项公式:若不存在,请说明理由.
的通项公式:若不存在,请说明理由.
您最近一年使用:0次
2019-09-23更新
|
561次组卷
|
5卷引用:重难点02数列求和的五种解题方法



