解题方法
1 . 已知随机变量X的分布列为
若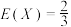 ,
,
(1)求 的值;
的值;
(2)若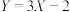 ,求
,求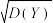 的值.
的值.
X | 0 | 1 | x |
P |
|
| p |
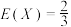 ,
,(1)求
 的值;
的值;(2)若
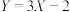 ,求
,求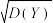 的值.
的值.
您最近一年使用:0次
2023-08-01更新
|
940次组卷
|
21卷引用:高中数学人教A版选修2-3 第二章 随机变量及其分布 2.3.2 离散型随机变量的方差
高中数学人教A版选修2-3 第二章 随机变量及其分布 2.3.2 离散型随机变量的方差西藏自治区拉萨市拉萨那曲第二高级中学2018-2019学年高二下学期期末数学(理)试题辽宁省葫芦岛市实验中学东戴河分校2019-2020学年高二下学期期中考试数学试题(已下线)突破2.3离散型随机变的均值与方差-突破满分数学之2019-2020学年高二数学(理)重难点突破(人教A版选修2-3)(已下线)专题14 计数原理、随机变量的数字特征 第一篇 热点、难点突破篇(讲)-2021年高考数学二轮复习讲练测(浙江专用)北师大版(2019) 选修第一册 突围者 第六章 第三节 课时2 离散型随机变量的方差(已下线)专题14 计数原理、随机变量的数字特征(讲)--第一篇 热点、难点突破篇-《2022年高考数学二轮复习讲练测(浙江专用)》6.3.2离散型随机变量的方差 同步练习6.3.2离散型随机变量的方差 课时作业新疆博湖县奇石中学2022-2023学年高二下学期期末考试数学试题(已下线)专题21 离散型随机变量的均值、方差与标准差(重点突围)-【学霸满分】2022-2023学年高二数学下学期重难点专题提优训练(苏教版2019选择性必修第二册)(已下线)第07讲 离散型随机变量的分布列与数字特征(六大题型)(讲义)(已下线)第10讲 离散型随机变量的均值与方差-【寒假预科讲义】2024年高二数学寒假精品课(人教A版2019)(已下线)专题12随机变量及其分布 (十六大题型+过关检测专训)(3)(已下线)专题12随机变量及其分布 (十六大题型+过关检测专训)(1)(已下线)第05讲 7.3.2离散型随机变量的方差-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第三册)(已下线)专题7.8 随机变量及其分布全章十一大压轴题型归纳(拔尖篇)-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)(已下线)第八章 概率(知识归纳+题型突破)-2023-2024学年高二数学单元速记·巧练(苏教版2019选择性必修第二册)(已下线)7.3.2 离散型随机变量的方差——课后作业(基础版)(已下线)第7.3.2讲 离散型随机变量的方差-2023-2024学年新高二数学同步精讲精练宝典(人教A版2019选修第三册)新疆兵团第三师图木舒克市鸿德实验学校2023-2024学年高二下学期第二次月考数学试卷
2020高三·全国·专题练习
名校
2 . 为迎接2022年北京冬奥会,推广滑雪运动,某滑雪场开展滑雪促销活动.该滑雪场的收费标准是:滑雪时间不超过1小时免费,超过1小时的部分每小时收费标准为40元(不足1小时的部分按1小时计算).有甲、乙两人相互独立地来该滑雪场运动,设甲、乙不超过1小时离开的概率分别为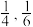 ;1小时以上且不超过2小时离开的概率分别为
;1小时以上且不超过2小时离开的概率分别为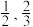 ;两人滑雪时间都不会超过3小时.
;两人滑雪时间都不会超过3小时.
(1)求甲、乙两人所付滑雪费用相同的概率;
(2)设甲、乙两人所付的滑雪费用之和为随机变量ξ,求ξ的分布列与均值E(ξ),方差D(ξ).
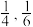 ;1小时以上且不超过2小时离开的概率分别为
;1小时以上且不超过2小时离开的概率分别为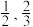 ;两人滑雪时间都不会超过3小时.
;两人滑雪时间都不会超过3小时.(1)求甲、乙两人所付滑雪费用相同的概率;
(2)设甲、乙两人所付的滑雪费用之和为随机变量ξ,求ξ的分布列与均值E(ξ),方差D(ξ).
您最近一年使用:0次
2022-11-08更新
|
2018次组卷
|
32卷引用:专题11.9 离散型随机变量的均值与方差(讲)【理】-《2020年高考一轮复习讲练测》
(已下线)专题11.9 离散型随机变量的均值与方差(讲)【理】-《2020年高考一轮复习讲练测》(已下线)专题06 离散型随机变量的期望与方差(第四篇)-备战2020年高考数学大题精做之解答题题型全覆盖山西省朔州市应县第一中学校2019-2020学年高二下学期期中数学(理)试题(已下线)专题11.5 离散型随机变量的分布列、均值与方差 (精讲)-2021年高考数学(理)一轮复习讲练测(已下线)7.3 离散型随机变量的数字特征(精讲)-2020-2021学年高二数学一隅三反系列(人教A版2019选择性必修第三册)(已下线)4.2.4随机变量的数字特征(2)B提高练(已下线)第二章 随机变量及其分布【专项训练】-2020-2021学年高二数学(理)下学期期末专项复习(人教A版选修2-3)(已下线)【新教材精创】7.3.2离散型随机变量的方差 -B提高练辽宁省凤城市第一中学2021-2022学年高三上学期10月月考数学试题人教A版(2019) 选修第三册 实战演练 第七章验收检测浙江省台州市九校联盟2021-2022学年高二下学期期中联考数学试题宁夏回族自治区银川一中2021-2022学年高二下学期期中考试数学(理)试题广东省佛山市南海一中2021-2022学年高二下学期第二次大测数学试题辽宁省沈阳市市级重点高中联合体2021-2022学年高二下学期期测试末数学试题江苏省苏州外国语学校2021-2022学年高二下学期期末数学试题(已下线)13.3 二项分布、超几何分布与数字特征(已下线)第70讲 随机变量及其概率分布、均值与方差(已下线)7.3.2离散型随机变量的方差(精讲)(已下线)第08讲 离散型随机变量的期望方差及其性质3种题型江苏省淮安市盱眙中学2023届高三七模数学试题(已下线)8.2.2离散型随机变量的数字特征-【帮课堂】2022-2023学年高二数学同步精品讲义(苏教版2019选择性必修第二册)(已下线)7.3.1 离散型随机变量的均值(2)(已下线)7.3.2 离散型随机变量的方差(2)(已下线)7.3.2 离散型随机变量的方差(1)北师大版(2019) 选修第一册 数学奇书 学业评价(四十二) 离散型随机变量的方差江西省上高二中2022-2023学年高二下学期2月月考数学试题(已下线)7.3离散型随机变量的数字特征 第二练 强化考点训练江苏省扬州市广陵区红桥高级中学2023-2024学年高二下学期期中考试数学试题湖北省荆州中学2024届高三下学期第三次适应性考试数学试题【江苏专用】专题08概率与统计(第五部分)-高二下学期名校期末好题汇编(已下线)专题05 离散型随机变量的分布列常考点(8类题型)-备战2023-2024学年高二数学下学期期末真题分类汇编(江苏专用)【基础卷】第7章 概率初步(续)单元测试C-沪教版(2020)选择性必修第二册
名校
解题方法
3 . 为了响应大学毕业生自主创业的号召,小李毕业后开了水果店,水果店每天以每个5元的价格从农场购进若干西瓜,然后以每个10元的价格出售.如果当天卖不完,剩下的西瓜作赠品处理.
(1)若水果店一天购进16个西瓜,求当天的利润 (单位:元)关于当天需求量
(单位:元)关于当天需求量 (单位:个,
(单位:个, )的函数解析式;
)的函数解析式;
(2)水果店记录了100天西瓜的日需求量(单位:个),整理得下表:
以100天记录的各需求量的频率作为各需求量发生的概率.
①若水果店一天购进16个西瓜, 表示当天的利润(单位:元),求
表示当天的利润(单位:元),求 的分布列、数学期望及方差;
的分布列、数学期望及方差;
②若水果店计划一天购进16个或17个西瓜,你认为应购进16个还是17个?请说明理由.
(1)若水果店一天购进16个西瓜,求当天的利润
 (单位:元)关于当天需求量
(单位:元)关于当天需求量 (单位:个,
(单位:个, )的函数解析式;
)的函数解析式;(2)水果店记录了100天西瓜的日需求量(单位:个),整理得下表:
日需求量 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
①若水果店一天购进16个西瓜,
 表示当天的利润(单位:元),求
表示当天的利润(单位:元),求 的分布列、数学期望及方差;
的分布列、数学期望及方差;②若水果店计划一天购进16个或17个西瓜,你认为应购进16个还是17个?请说明理由.
您最近一年使用:0次
2022-07-25更新
|
1052次组卷
|
15卷引用:广东省六校(广州二中,深圳实验,珠海一中,中山纪念,东莞中学,惠州一中)2018届高三下学期第三次联考数学(理)试题
广东省六校(广州二中,深圳实验,珠海一中,中山纪念,东莞中学,惠州一中)2018届高三下学期第三次联考数学(理)试题广东省珠海一中等六校2018届高三第三次联考数学理试题(已下线)2018年高考数学备考中等生百日捷进提升系列(综合提升篇) 专题02 概率统计解答题(理)河北省邯郸市永年区第二中学2019-2020学年高二下学期6月月考数学试题(已下线)专题11.7 计数原理、概率、随机变量及其分布列单元检测-2021年高考数学(理)一轮复习讲练测河北省武安市第一中学2020-2021学年高二下学期第三次月考数学试题(已下线)专题15 概率统计及其应用(练)--第一篇 热点、难点突破篇-《2022年高考数学二轮复习讲练测(新高考·全国卷)》陕西省宝鸡市金台区2021-2022学年高二下学期期末理科数学试题(已下线)第07讲 离散型随机变量及其分布列和数字特征 (精讲)(已下线)7.3.2离散型随机变量的方差(精讲)(已下线)第08讲 离散型随机变量的期望方差及其性质3种题型(已下线)7.3.2 离散型随机变量的方差(2)重庆巴蜀常春藤江南校区2022-2023学年高二下学期期中数学试题(已下线)专题7.8 随机变量及其分布全章十一大压轴题型归纳(拔尖篇)-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)(已下线)第五章 概率统计创新问题 专题一 概率统计决策问题 微点2 概率统计决策问题(二)【基础版】
名校
4 . 有甲、乙两家公司都需要招聘求职者,这两家公司的聘用信息如表所示.
(1)若一人去应聘甲公司的C职位,另一人去应聘乙公司的C职位,记这两人被录用的人数和为 ,求
,求 的分布列.
的分布列.
(2)若小方和小芳分别被甲、乙两家公司录用,求小方月薪高于小芳月薪的概率.
(3)根据甲、乙两家公司的聘用信息,如果你是求职者,你会选择哪一家公司?说明理由.
甲公司 | 乙公司 | ||||||||
职位 | A | B | C | D | 职位 | A | B | C | D |
月薪/千元 | 5 | 6 | 7 | 8 | 月薪/千元 | 4 | 6 | 8 | 10 |
获得相应职位概率 | 0.4 | 0.3 | 0.2 | 0.1 | 获得相应职位概率 | 0.4 | 0.3 | 0.2 | 0.1 |
 ,求
,求 的分布列.
的分布列.(2)若小方和小芳分别被甲、乙两家公司录用,求小方月薪高于小芳月薪的概率.
(3)根据甲、乙两家公司的聘用信息,如果你是求职者,你会选择哪一家公司?说明理由.
您最近一年使用:0次
2022-06-09更新
|
982次组卷
|
8卷引用:【校级联考】福建省三明市三地三校2018-2019学年高二下学期期中联考数学(理)试题
【校级联考】福建省三明市三地三校2018-2019学年高二下学期期中联考数学(理)试题北师大版(2019) 选修第一册 必杀技 第六章 素养检测人教A版(2019) 选修第三册 必杀技 第七章检测辽宁省渤海大学附属高级中学2021-2022学年高二4月份阶段性考试数学试题(已下线)第七章 随机变量及其分布 讲核心 01(已下线)第七章 随机变量及其分布 讲核心 02(已下线)7.3.2离散型随机变量的方差(精练)(已下线)第五章 概率统计创新问题 专题一 概率统计决策问题 微点1 概率统计决策问题(一)【基础版】
2010·湖北·一模
名校
解题方法
5 . 某公司计划在2022年年初将1000万元用于投资,现有两个项目供选择.项目一:新能源汽车.据市场调研,投资到该项目上,到年底可能获利30%,也可能亏损15%,且这两种情况发生的概率分别为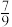 和
和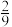 .项目二:通信设备.据市场调研,投资到该项目上,到年底可能获利50%,也可能亏损30%,也可能不赔不赚,且这三种情况发生的概率分别为
.项目二:通信设备.据市场调研,投资到该项目上,到年底可能获利50%,也可能亏损30%,也可能不赔不赚,且这三种情况发生的概率分别为 ,
, ,
, .
.
(1)针对以上两个投资项目,请你为投资公司选择一个合理的项目,并说明理由;
(2)若市场预期不变,该投资公司按照你选择的项目长期投资(每一年的利润和本金继续用作投资),问大约在哪一年的年底总资产(利润+本金)可以翻一番?(参考数据: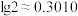 ,
,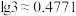 )
)
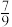 和
和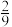 .项目二:通信设备.据市场调研,投资到该项目上,到年底可能获利50%,也可能亏损30%,也可能不赔不赚,且这三种情况发生的概率分别为
.项目二:通信设备.据市场调研,投资到该项目上,到年底可能获利50%,也可能亏损30%,也可能不赔不赚,且这三种情况发生的概率分别为 ,
, ,
, .
.(1)针对以上两个投资项目,请你为投资公司选择一个合理的项目,并说明理由;
(2)若市场预期不变,该投资公司按照你选择的项目长期投资(每一年的利润和本金继续用作投资),问大约在哪一年的年底总资产(利润+本金)可以翻一番?(参考数据:
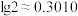 ,
,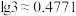 )
)
您最近一年使用:0次
2021-09-24更新
|
735次组卷
|
11卷引用:湖北襄樊四中2010年五月高考适应性考试数学试卷(理科)
(已下线)湖北襄樊四中2010年五月高考适应性考试数学试卷(理科)(已下线)福建省厦门双十中学2010届高三数学(理)热身考试卷(已下线)厦门双十中学2010届高三数学(理)热身考试卷2019届广西南宁市第二中学高三最后一模数学(理)试题人教A版(2019) 选修第三册 突围者 第七章 第三节 课时2 离散型随机变量的方差北师大版(2019) 选修第一册 突围者 第六章 第三节 课时2 离散型随机变量的方差(已下线)7.3离散型随机变量的数字特征C卷(已下线)13.3 二项分布、超几何分布与数字特征(已下线)第七章 随机变量及其分布 全章总结 (精讲)(2)第六章 概率单元检测B卷(综合篇)(已下线)第五章 概率统计创新问题 专题一 概率统计决策问题 微点1 概率统计决策问题(一)【基础版】
6 . 在全球关注的抗击“新冠肺炎”中,某跨国科研中心的一个团队,研制了甲、乙两种治疗“新冠肺炎”新药,希望知道哪种新药更有效,为此进行动物试验,试验方案如下:
第一种:选取 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, 共10只患病白鼠,服用甲药后某项指标分别为:84,87,89,91,92,92,86,89,90,90;
共10只患病白鼠,服用甲药后某项指标分别为:84,87,89,91,92,92,86,89,90,90;
第二种:选取 ,
, ,
, ,
, ,
, ,
, ,
,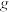 ,
, ,
, ,
, 共10只患病白鼠,服用乙药后某项指标分别为:81,87,83,82,80,90,86,89,84,79;
共10只患病白鼠,服用乙药后某项指标分别为:81,87,83,82,80,90,86,89,84,79;
该团队判定患病白鼠服药后这项指标不低于85的确认为药物有效,否则确认为药物无效.
(1)已知第一种试验方案的10个数据的平均数为89,求这组数据的方差;
(2)现需要从已服用乙药的10只白鼠中随机抽取7只,求其中服药有效的只数不超过2只的概率;
(3)该团队的另一实验室有1000只白鼠,其中900只为正常白鼠,100只为患病白鼠,每用新研制的甲药给所有患病白鼠服用一次,患病白鼠中有90%变为正常白鼠,但正常白鼠仍有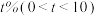 变为患病白鼠,假设实验室的所有白鼠都活着且数量不变,且记服用
变为患病白鼠,假设实验室的所有白鼠都活着且数量不变,且记服用 次甲药后此实验室正常白鼠的只数为
次甲药后此实验室正常白鼠的只数为 .
.
(ⅰ)求 并写出
并写出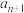 与
与 的关系式;
的关系式;
(ⅱ)要使服用甲药两次后,该实验室正常白鼠至少有950只,求最大的正整数 的值.
的值.
第一种:选取
 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, 共10只患病白鼠,服用甲药后某项指标分别为:84,87,89,91,92,92,86,89,90,90;
共10只患病白鼠,服用甲药后某项指标分别为:84,87,89,91,92,92,86,89,90,90;第二种:选取
 ,
, ,
, ,
, ,
, ,
, ,
,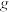 ,
, ,
, ,
, 共10只患病白鼠,服用乙药后某项指标分别为:81,87,83,82,80,90,86,89,84,79;
共10只患病白鼠,服用乙药后某项指标分别为:81,87,83,82,80,90,86,89,84,79;该团队判定患病白鼠服药后这项指标不低于85的确认为药物有效,否则确认为药物无效.
(1)已知第一种试验方案的10个数据的平均数为89,求这组数据的方差;
(2)现需要从已服用乙药的10只白鼠中随机抽取7只,求其中服药有效的只数不超过2只的概率;
(3)该团队的另一实验室有1000只白鼠,其中900只为正常白鼠,100只为患病白鼠,每用新研制的甲药给所有患病白鼠服用一次,患病白鼠中有90%变为正常白鼠,但正常白鼠仍有
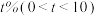 变为患病白鼠,假设实验室的所有白鼠都活着且数量不变,且记服用
变为患病白鼠,假设实验室的所有白鼠都活着且数量不变,且记服用 次甲药后此实验室正常白鼠的只数为
次甲药后此实验室正常白鼠的只数为 .
.(ⅰ)求
 并写出
并写出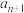 与
与 的关系式;
的关系式;(ⅱ)要使服用甲药两次后,该实验室正常白鼠至少有950只,求最大的正整数
 的值.
的值.
您最近一年使用:0次
名校
解题方法
7 . 某超市试销某种商品一个月,获得如下数据:
试销结束后(假设该商品的日销售量的分布规律不变),超市决定正式营销这种商品.设某天超市开始营业时有该商品 件,当天营业结束后检查存货,若发现存货少于
件,当天营业结束后检查存货,若发现存货少于 件,则当天进货补充至
件,则当天进货补充至 件,否则不进货.将频率视为概率.
件,否则不进货.将频率视为概率.
 求当天商品进货的概率.
求当天商品进货的概率.
 记
记 为第二天开始营业时该商品的件数.
为第二天开始营业时该商品的件数.
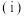 求
求 得分布列.
得分布列.
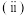 求
求 得数学期望与方差.
得数学期望与方差.
| 日销售量(件) |  |  |  |  |  |
| 频率 |  |  |  |  |  |
试销结束后(假设该商品的日销售量的分布规律不变),超市决定正式营销这种商品.设某天超市开始营业时有该商品
 件,当天营业结束后检查存货,若发现存货少于
件,当天营业结束后检查存货,若发现存货少于 件,则当天进货补充至
件,则当天进货补充至 件,否则不进货.将频率视为概率.
件,否则不进货.将频率视为概率. 求当天商品进货的概率.
求当天商品进货的概率. 记
记 为第二天开始营业时该商品的件数.
为第二天开始营业时该商品的件数.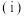 求
求 得分布列.
得分布列.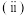 求
求 得数学期望与方差.
得数学期望与方差.
您最近一年使用:0次
名校
8 . 为了解某地区初中学生的体质健康情况,统计了该地区8所学校学生的体质健康数据,按总分评定等级为优秀,良好,及格,不及格.良好及其以上的比例之和超过40%的学校为先进校.各等级学生人数占该校学生总人数的比例如下表:
(1)从8所学校中随机选出一所学校,求该校为先进校的概率;
(2)从8所学校中随机选出两所学校,记这两所学校中不及格比例低于30%的学校个数为X,求X的分布列;
(3)设8所学校优秀比例的方差为 ,良好及其以下比例之和的方差为
,良好及其以下比例之和的方差为 ,比较
,比较 与
与 的大小.(只写出结果)
的大小.(只写出结果)
| 比例 学校 等级 | 学校A | 学校B | 学校C | 学校D | 学校E | 学校F | 学校G | 学校H |
| 优秀 | 8% | 3% | 2% | 9% | 1% | 22% | 2% | 3% |
| 良好 | 37% | 50% | 23% | 30% | 45% | 46% | 37% | 35% |
| 及格 | 22% | 30% | 33% | 26% | 22% | 17% | 23% | 38% |
| 不及格 | 33% | 17% | 42% | 35% | 32% | 15% | 38% | 24% |
(1)从8所学校中随机选出一所学校,求该校为先进校的概率;
(2)从8所学校中随机选出两所学校,记这两所学校中不及格比例低于30%的学校个数为X,求X的分布列;
(3)设8所学校优秀比例的方差为
 ,良好及其以下比例之和的方差为
,良好及其以下比例之和的方差为 ,比较
,比较 与
与 的大小.(只写出结果)
的大小.(只写出结果)
您最近一年使用:0次
2020-02-09更新
|
519次组卷
|
8卷引用:2020届北京市通州区高三第一学期期末考试数学试题
2020届北京市通州区高三第一学期期末考试数学试题2020届山东省济宁市嘉祥一中高三下学期第一次质量检测数学试题(已下线)专题01 少丢分题目强化卷(第二篇)-备战2021年新高考数学分层强化训练(北京专版)(已下线)专题03 少丢分题目强化卷(第二篇)-备战2021年新高考数学分层强化训练(北京专版)人教B版(2019) 选择性必修第二册 过关斩将 第四章 概率与统计 4.2 随机变量 专题强化练5 离散型随机变量的分布列及数字特征(已下线)专题10 必拿分题目强化卷(第一篇)-备战2021年新高考数学分层强化训练(北京专版)陕西省咸阳市武功县普集高中2021-2022学年高一重点班下学期第一次月考数学试题北京市北京师范大学第二附属中学2023-2024学年高二下学期第二次月考数学试题
9 . 一个小商店从一家有限公司购进21袋白糖,每袋白糖的标准质量是500g,为了了解这些白糖的质量情况,称出各袋白糖的质量(单位:g)如下:
486 495 496 498 499 493 493 498 484 497 504 489 495 503
499 503 509 498 487 500 508
(1)21袋白糖的平均质量是多少?标准差s是多少?
(2)质量位于 与
与 之间有多少袋白糖?所占的百分比是多少?
之间有多少袋白糖?所占的百分比是多少?
486 495 496 498 499 493 493 498 484 497 504 489 495 503
499 503 509 498 487 500 508
(1)21袋白糖的平均质量是多少?标准差s是多少?
(2)质量位于
 与
与 之间有多少袋白糖?所占的百分比是多少?
之间有多少袋白糖?所占的百分比是多少?
您最近一年使用:0次
2020-02-01更新
|
205次组卷
|
3卷引用:人教A版(2019) 必修第二册 逆袭之路 第九章 9.2 用样本估计总体 9.2.4 总体离散程度的估计
人教A版(2019) 必修第二册 逆袭之路 第九章 9.2 用样本估计总体 9.2.4 总体离散程度的估计人教A版(2019)必修第二册课本习题9.2 用样本估计总体(已下线)9.2.4总体离散程度的估计(导学案)-【上好课】(人教A版2019选择性必修第二册)
10 . 本小题满分12分)根据以往的经验,某工程施工期间的降水量X(单位:mm)对工期的影响如下表:
历年气象资料表明,该工程施工期间降水量X小于300,700,900的概率分别为0.3,0.7,0.9. 求:
(Ⅰ)工期延误天数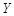 的均值与方差;
的均值与方差;
(Ⅱ)在降水量X至少是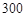 的条件下,工期延误不超过6天的概率.
的条件下,工期延误不超过6天的概率.
| 降水量X | 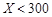 |  | 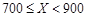 |  |
工期延误天数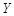 | 0 | 2 | 6 | 10 |
(Ⅰ)工期延误天数
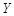 的均值与方差;
的均值与方差; (Ⅱ)在降水量X至少是
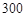 的条件下,工期延误不超过6天的概率.
的条件下,工期延误不超过6天的概率.
您最近一年使用:0次
2019-01-30更新
|
2585次组卷
|
18卷引用:2012年全国普通高等学校招生统一考试理科数学(湖北卷)
2012年全国普通高等学校招生统一考试理科数学(湖北卷)(已下线)2014高考名师推荐数学理科正态分布2015届吉林省实验中学高三上学期第五次模拟考试理科数学试卷2016届河南省南阳、周口、驻马店等六市高三第一次联考理科数学试卷2015-2016新疆哈密地区二中高二下期末考试理科数学卷内蒙古包头市第一中学2016-2017学年高二下学期期中考试数学(理)试题重庆市凤鸣山中学2019-2020学年高二下学期6月月考数学试题(已下线)7.3.2 离散型随机变量的方差(练习)-2020-2021学年下学期高二数学同步精品课堂(新教材人教A版选择性必修第三册)(已下线)专题7.3离散型随机变量的数字特征(A卷基础篇)-2020-2021学年高二下学期数学选择性必修第三册同步单元AB卷(新教材人教A版,浙江专用)人教A版(2019) 选修第三册 突围者 第七章 第三节 课时2 离散型随机变量的方差黑龙江省牡丹江市第二高级中学2022-2023学年高三上学期第二次阶段测试数学试题6.3.2离散型随机变量的方差 同步练习6.3.2离散型随机变量的方差 课时作业北师大版(2019) 选修第一册 章末检测卷(五) 概率河北省秦皇岛市卢龙县第二高级中学2023-2024学年高二下学期3月月考数学试题四川省绵阳市东辰学校2024届高三下学期第二学月考试数学(理科)试题四川省成都市金堂县淮口中学校2024届高三下学高考仿真冲刺卷(一)理科数学试题【基础卷】第7章 概率初步(续)单元测试C-沪教版(2020)选择性必修第二册




