解题方法
1 . 已知随机变量X的分布列为
若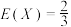 ,
,
(1)求 的值;
的值;
(2)若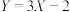 ,求
,求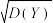 的值.
的值.
X | 0 | 1 | x |
P |
|
| p |
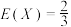 ,
,(1)求
 的值;
的值;(2)若
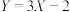 ,求
,求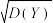 的值.
的值.
您最近一年使用:0次
2023-08-01更新
|
940次组卷
|
21卷引用:西藏自治区拉萨市拉萨那曲第二高级中学2018-2019学年高二下学期期末数学(理)试题
西藏自治区拉萨市拉萨那曲第二高级中学2018-2019学年高二下学期期末数学(理)试题高中数学人教A版选修2-3 第二章 随机变量及其分布 2.3.2 离散型随机变量的方差辽宁省葫芦岛市实验中学东戴河分校2019-2020学年高二下学期期中考试数学试题(已下线)突破2.3离散型随机变的均值与方差-突破满分数学之2019-2020学年高二数学(理)重难点突破(人教A版选修2-3)新疆博湖县奇石中学2022-2023学年高二下学期期末考试数学试题(已下线)专题14 计数原理、随机变量的数字特征 第一篇 热点、难点突破篇(讲)-2021年高考数学二轮复习讲练测(浙江专用)北师大版(2019) 选修第一册 突围者 第六章 第三节 课时2 离散型随机变量的方差(已下线)专题14 计数原理、随机变量的数字特征(讲)--第一篇 热点、难点突破篇-《2022年高考数学二轮复习讲练测(浙江专用)》6.3.2离散型随机变量的方差 同步练习6.3.2离散型随机变量的方差 课时作业(已下线)专题21 离散型随机变量的均值、方差与标准差(重点突围)-【学霸满分】2022-2023学年高二数学下学期重难点专题提优训练(苏教版2019选择性必修第二册)(已下线)第07讲 离散型随机变量的分布列与数字特征(六大题型)(讲义)(已下线)第10讲 离散型随机变量的均值与方差-【寒假预科讲义】2024年高二数学寒假精品课(人教A版2019)(已下线)专题12随机变量及其分布 (十六大题型+过关检测专训)(3)(已下线)专题12随机变量及其分布 (十六大题型+过关检测专训)(1)(已下线)第05讲 7.3.2离散型随机变量的方差-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第三册)(已下线)专题7.8 随机变量及其分布全章十一大压轴题型归纳(拔尖篇)-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)(已下线)第八章 概率(知识归纳+题型突破)-2023-2024学年高二数学单元速记·巧练(苏教版2019选择性必修第二册)(已下线)7.3.2 离散型随机变量的方差——课后作业(基础版)(已下线)第7.3.2讲 离散型随机变量的方差-2023-2024学年新高二数学同步精讲精练宝典(人教A版2019选修第三册)新疆兵团第三师图木舒克市鸿德实验学校2023-2024学年高二下学期第二次月考数学试卷
2020高三·全国·专题练习
名校
2 . 为迎接2022年北京冬奥会,推广滑雪运动,某滑雪场开展滑雪促销活动.该滑雪场的收费标准是:滑雪时间不超过1小时免费,超过1小时的部分每小时收费标准为40元(不足1小时的部分按1小时计算).有甲、乙两人相互独立地来该滑雪场运动,设甲、乙不超过1小时离开的概率分别为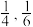 ;1小时以上且不超过2小时离开的概率分别为
;1小时以上且不超过2小时离开的概率分别为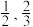 ;两人滑雪时间都不会超过3小时.
;两人滑雪时间都不会超过3小时.
(1)求甲、乙两人所付滑雪费用相同的概率;
(2)设甲、乙两人所付的滑雪费用之和为随机变量ξ,求ξ的分布列与均值E(ξ),方差D(ξ).
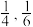 ;1小时以上且不超过2小时离开的概率分别为
;1小时以上且不超过2小时离开的概率分别为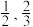 ;两人滑雪时间都不会超过3小时.
;两人滑雪时间都不会超过3小时.(1)求甲、乙两人所付滑雪费用相同的概率;
(2)设甲、乙两人所付的滑雪费用之和为随机变量ξ,求ξ的分布列与均值E(ξ),方差D(ξ).
您最近一年使用:0次
2022-11-08更新
|
2018次组卷
|
32卷引用:专题11.9 离散型随机变量的均值与方差(讲)【理】-《2020年高考一轮复习讲练测》
(已下线)专题11.9 离散型随机变量的均值与方差(讲)【理】-《2020年高考一轮复习讲练测》(已下线)专题06 离散型随机变量的期望与方差(第四篇)-备战2020年高考数学大题精做之解答题题型全覆盖山西省朔州市应县第一中学校2019-2020学年高二下学期期中数学(理)试题(已下线)专题11.5 离散型随机变量的分布列、均值与方差 (精讲)-2021年高考数学(理)一轮复习讲练测辽宁省沈阳市市级重点高中联合体2021-2022学年高二下学期期测试末数学试题江苏省苏州外国语学校2021-2022学年高二下学期期末数学试题(已下线)7.3 离散型随机变量的数字特征(精讲)-2020-2021学年高二数学一隅三反系列(人教A版2019选择性必修第三册)(已下线)4.2.4随机变量的数字特征(2)B提高练(已下线)第二章 随机变量及其分布【专项训练】-2020-2021学年高二数学(理)下学期期末专项复习(人教A版选修2-3)(已下线)【新教材精创】7.3.2离散型随机变量的方差 -B提高练辽宁省凤城市第一中学2021-2022学年高三上学期10月月考数学试题人教A版(2019) 选修第三册 实战演练 第七章验收检测浙江省台州市九校联盟2021-2022学年高二下学期期中联考数学试题宁夏回族自治区银川一中2021-2022学年高二下学期期中考试数学(理)试题广东省佛山市南海一中2021-2022学年高二下学期第二次大测数学试题(已下线)13.3 二项分布、超几何分布与数字特征(已下线)第70讲 随机变量及其概率分布、均值与方差(已下线)7.3.2离散型随机变量的方差(精讲)(已下线)第08讲 离散型随机变量的期望方差及其性质3种题型江苏省淮安市盱眙中学2023届高三七模数学试题(已下线)8.2.2离散型随机变量的数字特征-【帮课堂】2022-2023学年高二数学同步精品讲义(苏教版2019选择性必修第二册)(已下线)7.3.1 离散型随机变量的均值(2)(已下线)7.3.2 离散型随机变量的方差(2)(已下线)7.3.2 离散型随机变量的方差(1)北师大版(2019) 选修第一册 数学奇书 学业评价(四十二) 离散型随机变量的方差江西省上高二中2022-2023学年高二下学期2月月考数学试题(已下线)7.3离散型随机变量的数字特征 第二练 强化考点训练江苏省扬州市广陵区红桥高级中学2023-2024学年高二下学期期中考试数学试题湖北省荆州中学2024届高三下学期第三次适应性考试数学试题【江苏专用】专题08概率与统计(第五部分)-高二下学期名校期末好题汇编(已下线)专题05 离散型随机变量的分布列常考点(8类题型)-备战2023-2024学年高二数学下学期期末真题分类汇编(江苏专用)【基础卷】第7章 概率初步(续)单元测试C-沪教版(2020)选择性必修第二册
名校
解题方法
3 . 为了响应大学毕业生自主创业的号召,小李毕业后开了水果店,水果店每天以每个5元的价格从农场购进若干西瓜,然后以每个10元的价格出售.如果当天卖不完,剩下的西瓜作赠品处理.
(1)若水果店一天购进16个西瓜,求当天的利润 (单位:元)关于当天需求量
(单位:元)关于当天需求量 (单位:个,
(单位:个, )的函数解析式;
)的函数解析式;
(2)水果店记录了100天西瓜的日需求量(单位:个),整理得下表:
以100天记录的各需求量的频率作为各需求量发生的概率.
①若水果店一天购进16个西瓜, 表示当天的利润(单位:元),求
表示当天的利润(单位:元),求 的分布列、数学期望及方差;
的分布列、数学期望及方差;
②若水果店计划一天购进16个或17个西瓜,你认为应购进16个还是17个?请说明理由.
(1)若水果店一天购进16个西瓜,求当天的利润
 (单位:元)关于当天需求量
(单位:元)关于当天需求量 (单位:个,
(单位:个, )的函数解析式;
)的函数解析式;(2)水果店记录了100天西瓜的日需求量(单位:个),整理得下表:
日需求量 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
①若水果店一天购进16个西瓜,
 表示当天的利润(单位:元),求
表示当天的利润(单位:元),求 的分布列、数学期望及方差;
的分布列、数学期望及方差;②若水果店计划一天购进16个或17个西瓜,你认为应购进16个还是17个?请说明理由.
您最近一年使用:0次
2022-07-25更新
|
1052次组卷
|
15卷引用:广东省六校(广州二中,深圳实验,珠海一中,中山纪念,东莞中学,惠州一中)2018届高三下学期第三次联考数学(理)试题
广东省六校(广州二中,深圳实验,珠海一中,中山纪念,东莞中学,惠州一中)2018届高三下学期第三次联考数学(理)试题广东省珠海一中等六校2018届高三第三次联考数学理试题(已下线)2018年高考数学备考中等生百日捷进提升系列(综合提升篇) 专题02 概率统计解答题(理)河北省邯郸市永年区第二中学2019-2020学年高二下学期6月月考数学试题(已下线)专题11.7 计数原理、概率、随机变量及其分布列单元检测-2021年高考数学(理)一轮复习讲练测陕西省宝鸡市金台区2021-2022学年高二下学期期末理科数学试题河北省武安市第一中学2020-2021学年高二下学期第三次月考数学试题(已下线)专题15 概率统计及其应用(练)--第一篇 热点、难点突破篇-《2022年高考数学二轮复习讲练测(新高考·全国卷)》(已下线)第07讲 离散型随机变量及其分布列和数字特征 (精讲)(已下线)7.3.2离散型随机变量的方差(精讲)(已下线)第08讲 离散型随机变量的期望方差及其性质3种题型(已下线)7.3.2 离散型随机变量的方差(2)重庆巴蜀常春藤江南校区2022-2023学年高二下学期期中数学试题(已下线)专题7.8 随机变量及其分布全章十一大压轴题型归纳(拔尖篇)-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)(已下线)第五章 概率统计创新问题 专题一 概率统计决策问题 微点2 概率统计决策问题(二)【基础版】
名校
解题方法
4 . 甲口袋里有大小相同编号不同的2个黑球和3个白球,乙口袋里有大小相同编号不同的3个黑球和2个白球,现从甲口袋中取出3个球,记黑球个数为 ,从乙口袋中也取出3个球,记黑球个数为
,从乙口袋中也取出3个球,记黑球个数为 .
.
(1)求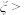
 时的概率;
时的概率;
(2)若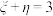 ,求随机变量
,求随机变量 的数学期望
的数学期望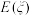 及
及 的方差
的方差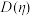 .
.
 ,从乙口袋中也取出3个球,记黑球个数为
,从乙口袋中也取出3个球,记黑球个数为 .
.(1)求
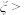
 时的概率;
时的概率;(2)若
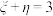 ,求随机变量
,求随机变量 的数学期望
的数学期望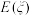 及
及 的方差
的方差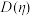 .
.
您最近一年使用:0次
名校
解题方法
5 . 旅游公司为3个旅游团提供甲、乙、丙、丁4条旅游线路,每个旅游团任选其中一条.
(1)求3个旅游团选择3条不同的线路的概率;
(2)求选择甲线路旅游团数的分布列、均值 及方差.
及方差.
(1)求3个旅游团选择3条不同的线路的概率;
(2)求选择甲线路旅游团数的分布列、均值
 及方差.
及方差.
您最近一年使用:0次
2021-08-24更新
|
139次组卷
|
2卷引用:新疆新源县第二中学2018-2019学年高二下学期期末考试数学(理)试题
名校
解题方法
6 . 某市电视台举办纪念红军长征胜利知识回答活动,宣传长征精神,首先在甲、乙、丙、丁四个不同的公园进行支持签名活动.
然后在各公园签名的人中按分层抽样的方式抽取10名幸运之星回答问题,从10个关于长征的问题中随机抽取4个问题让幸运之星回答,全部答对的幸运之星获得一份纪念品.
(1)求此活动中各公园幸运之星的人数;
(2)若乙公园中每位幸运之星对每个问题答对的概率均为 ,求乙公园中恰好2位幸运之星获得纪念品的概率;
,求乙公园中恰好2位幸运之星获得纪念品的概率;
(3)若幸运之星小李对其中8个问题能答对,而另外2个问题答不对,记小李答对的问题数为 ,求
,求 的分布列、期望及方差.
的分布列、期望及方差.
公园 | 甲 | 乙 | 丙 | 丁 |
获得签名人数 | 45 | 60 | 30 | 15 |
(1)求此活动中各公园幸运之星的人数;
(2)若乙公园中每位幸运之星对每个问题答对的概率均为
 ,求乙公园中恰好2位幸运之星获得纪念品的概率;
,求乙公园中恰好2位幸运之星获得纪念品的概率;(3)若幸运之星小李对其中8个问题能答对,而另外2个问题答不对,记小李答对的问题数为
 ,求
,求 的分布列、期望及方差.
的分布列、期望及方差.
您最近一年使用:0次
2020-08-03更新
|
308次组卷
|
2卷引用:甘肃省武威市民勤县第一中学2019-2020学年高二第二学期期末考试数学(理科)试题
7 . 2020突如其来的疫情让我们经历了最漫长、最特殊的一个假期,教育行政部门部署了“停课不停学”的行动,全力帮助学生在线学习.复课后某校进行了摸底考试,某数学教师为了调查高二学生这次摸底考试的数学成绩与每天在线学习数学的时长之间的相关关系,对在校高二学生随机抽取45名进行调查,了解到其中有25人每天在线学习数学的时长不超过1小时,并得到如下的等高条形图:

(1)根据等高条形图填写下面 列联表,并根据列联表判断能否在犯错误的概率不超过0.05的前提下认为“高二学生的这次摸底考试数学成绩与其每天在线学习数学的时长有关”;
列联表,并根据列联表判断能否在犯错误的概率不超过0.05的前提下认为“高二学生的这次摸底考试数学成绩与其每天在线学习数学的时长有关”;
(2)从被抽查的,且这次数学成绩超过120分的学生中,再随机抽取3人,求抽取的3人中每天在线学习数学的时长超过1小时的人数 的分布列与数学期望.
的分布列与数学期望.
附临界值表
参考公式: ,其中
,其中 .
.

(1)根据等高条形图填写下面
 列联表,并根据列联表判断能否在犯错误的概率不超过0.05的前提下认为“高二学生的这次摸底考试数学成绩与其每天在线学习数学的时长有关”;
列联表,并根据列联表判断能否在犯错误的概率不超过0.05的前提下认为“高二学生的这次摸底考试数学成绩与其每天在线学习数学的时长有关”;数学成绩不超过120分 | 数学成绩超过120分 | 总计 | |
每天在线学习数学不超过1小时 | 25 | ||
每天在线学习数学超过1小时 | |||
总计 | 45 |
(2)从被抽查的,且这次数学成绩超过120分的学生中,再随机抽取3人,求抽取的3人中每天在线学习数学的时长超过1小时的人数
 的分布列与数学期望.
的分布列与数学期望.附临界值表
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
参考公式:
 ,其中
,其中 .
.
您最近一年使用:0次
8 . 某地区为了解党员同志每天的学习强国的积分情况,抽取了20名同志,其中男同志10名,女同志10名,他们的积分用茎叶图表示如下:积分在40分(含40分)以上的为积极学习的党员同志.
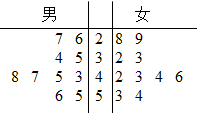
(1)求出男同志学习强国积分的平均值和女同志积极学习的频率,
(2)用频率估计概率,从该地区随机抽取3名党员,设积极学习的党员同志人数为 ,求
,求 的数学期望和方差.
的数学期望和方差.

(1)求出男同志学习强国积分的平均值和女同志积极学习的频率,
(2)用频率估计概率,从该地区随机抽取3名党员,设积极学习的党员同志人数为
 ,求
,求 的数学期望和方差.
的数学期望和方差.
您最近一年使用:0次
2020-07-28更新
|
246次组卷
|
2卷引用:广东省地市级2019-2020学年高二(下)期末数学试题
9 . 1933年7月11日,中华苏维埃共和国临时中央政府根据中央革命军事委员会6月30日的建议,决定8月1日为中国工农红军成立纪念日,中华人民共和国成立后,将此纪念日改称为中国人民解放军建军节.为庆祝建军节,某校举行“强国强军”知识竞赛,该校某班经过层层筛选,还有最后一个参赛名额要在 ,
, 两名学生中间产生,该班委设计了一个测试方案:
两名学生中间产生,该班委设计了一个测试方案: ,
, 两名学生各自从6个问题中随机抽取3个问题作答.已知这6个问题中,学生
两名学生各自从6个问题中随机抽取3个问题作答.已知这6个问题中,学生 能正确回答其中的4个问题,而学生
能正确回答其中的4个问题,而学生 能正确回答每个问题的概率均为
能正确回答每个问题的概率均为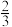 ,
, ,
, 两名学生对每个问题回答正确与否都是相互独立、互不影响的.
两名学生对每个问题回答正确与否都是相互独立、互不影响的.
(1)求 恰好答对两个问题的概率;
恰好答对两个问题的概率;
(2)求 恰好答对两个问题的概率;
恰好答对两个问题的概率;
(3)设 答对题数为
答对题数为 ,
, 答对题数为
答对题数为 ,若让你投票决定参赛选手,你会选择哪名学生?请说明理由.
,若让你投票决定参赛选手,你会选择哪名学生?请说明理由.
 ,
, 两名学生中间产生,该班委设计了一个测试方案:
两名学生中间产生,该班委设计了一个测试方案: ,
, 两名学生各自从6个问题中随机抽取3个问题作答.已知这6个问题中,学生
两名学生各自从6个问题中随机抽取3个问题作答.已知这6个问题中,学生 能正确回答其中的4个问题,而学生
能正确回答其中的4个问题,而学生 能正确回答每个问题的概率均为
能正确回答每个问题的概率均为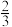 ,
, ,
, 两名学生对每个问题回答正确与否都是相互独立、互不影响的.
两名学生对每个问题回答正确与否都是相互独立、互不影响的.(1)求
 恰好答对两个问题的概率;
恰好答对两个问题的概率;(2)求
 恰好答对两个问题的概率;
恰好答对两个问题的概率;(3)设
 答对题数为
答对题数为 ,
, 答对题数为
答对题数为 ,若让你投票决定参赛选手,你会选择哪名学生?请说明理由.
,若让你投票决定参赛选手,你会选择哪名学生?请说明理由.
您最近一年使用:0次
2020-07-27更新
|
443次组卷
|
4卷引用:山东省枣庄市2019-2020学年高二(下)期末数学试题
山东省枣庄市2019-2020学年高二(下)期末数学试题山东省枣庄市2019—2020学年度高二年级第二学期期末考试数学试题(已下线)7.4 二项分布与超几何分布(精练)-2020-2021学年高二数学一隅三反系列(人教A版2019选择性必修第三册)(已下线)4.2.4随机变量的数字特征(2)A基础练
名校
10 . 某投资公司在2020年年初准备将1000万元投资到“低碳”项目上,现有两个项目供选择:
项目一:新能源汽车.据市场调研,投资到该项目上,到年底可能获利40%,也可能亏损10%,且这两种情况发生的概率分别为 和
和 ;
;
项目二:通信设备据市场调研,投资到该项目上,到年底可能获利50%,可能损失30%,也可能不赔不赚,且这三种情况发生的概率分别为 ,
, 和
和 .针对以上两个投资项目,请你为投资公司选择一个合理的项目,并说明理由.
.针对以上两个投资项目,请你为投资公司选择一个合理的项目,并说明理由.
项目一:新能源汽车.据市场调研,投资到该项目上,到年底可能获利40%,也可能亏损10%,且这两种情况发生的概率分别为
 和
和 ;
;项目二:通信设备据市场调研,投资到该项目上,到年底可能获利50%,可能损失30%,也可能不赔不赚,且这三种情况发生的概率分别为
 ,
, 和
和 .针对以上两个投资项目,请你为投资公司选择一个合理的项目,并说明理由.
.针对以上两个投资项目,请你为投资公司选择一个合理的项目,并说明理由.
您最近一年使用:0次
2020-07-05更新
|
1492次组卷
|
4卷引用:山东省泰安市新泰一中2019-2020学年高二下第一次质量检测考试数学试题
山东省泰安市新泰一中2019-2020学年高二下第一次质量检测考试数学试题(已下线)考点39 均值与方差在生活中运用(讲解)-2021年高考数学复习一轮复习笔记(已下线)模块二 专题3 概率与统计中决策问题人教A版(2019) 选修第三册 实战演练 第七章 7.3 课时练习12 离散型随机变量的方差






